Question Number 54562 by Meritguide1234 last updated on 06/Feb/19

Answered by JDamian last updated on 07/Feb/19
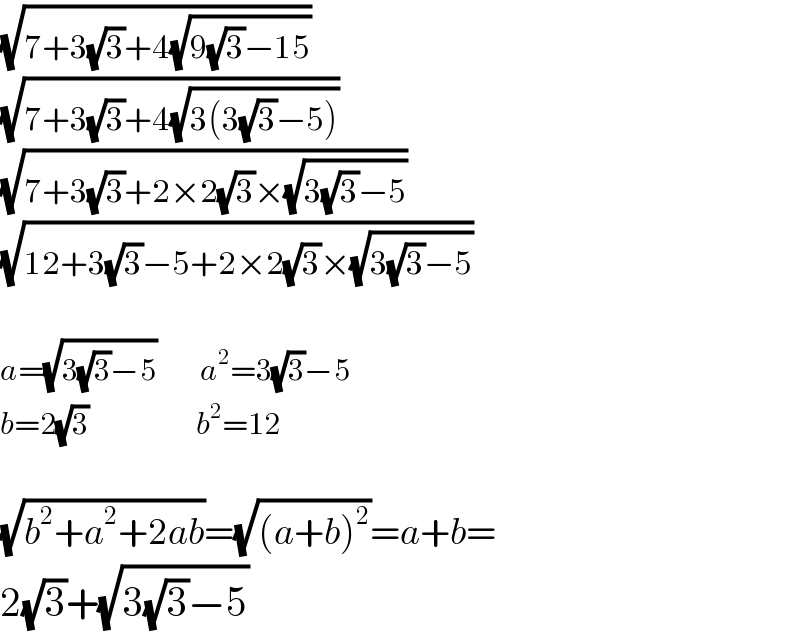
$$\sqrt{\mathrm{7}+\mathrm{3}\sqrt{\mathrm{3}}+\mathrm{4}\sqrt{\mathrm{9}\sqrt{\mathrm{3}}−\mathrm{15}}} \\ $$$$\sqrt{\mathrm{7}+\mathrm{3}\sqrt{\mathrm{3}}+\mathrm{4}\sqrt{\mathrm{3}\left(\mathrm{3}\sqrt{\mathrm{3}}−\mathrm{5}\right)}} \\ $$$$\sqrt{\mathrm{7}+\mathrm{3}\sqrt{\mathrm{3}}+\mathrm{2}×\mathrm{2}\sqrt{\mathrm{3}}×\sqrt{\mathrm{3}\sqrt{\mathrm{3}}−\mathrm{5}}} \\ $$$$\sqrt{\mathrm{12}+\mathrm{3}\sqrt{\mathrm{3}}−\mathrm{5}+\mathrm{2}×\mathrm{2}\sqrt{\mathrm{3}}×\sqrt{\mathrm{3}\sqrt{\mathrm{3}}−\mathrm{5}}} \\ $$$$ \\ $$$${a}=\sqrt{\mathrm{3}\sqrt{\mathrm{3}}−\mathrm{5}}\:\:\:\:\:\:\:{a}^{\mathrm{2}} =\mathrm{3}\sqrt{\mathrm{3}}−\mathrm{5} \\ $$$${b}=\mathrm{2}\sqrt{\mathrm{3}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{b}^{\mathrm{2}} =\mathrm{12} \\ $$$$ \\ $$$$\sqrt{{b}^{\mathrm{2}} +{a}^{\mathrm{2}} +\mathrm{2}{ab}}=\sqrt{\left({a}+{b}\right)^{\mathrm{2}} }={a}+{b}= \\ $$$$\mathrm{2}\sqrt{\mathrm{3}}+\sqrt{\mathrm{3}\sqrt{\mathrm{3}}−\mathrm{5}} \\ $$
