Question Number 54616 by cesar.marval.larez@gmail.com last updated on 07/Feb/19
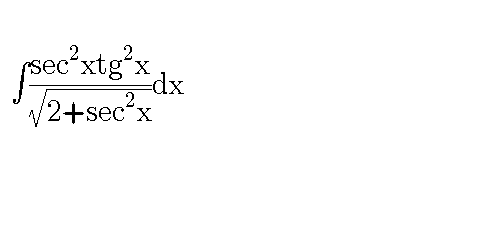
Answered by tanmay.chaudhury50@gmail.com last updated on 08/Feb/19
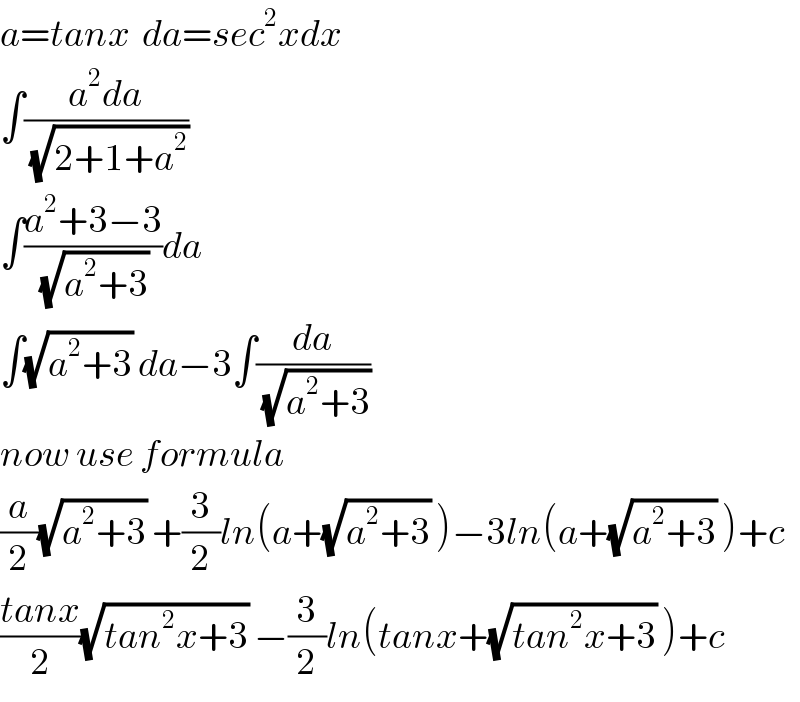
$${a}={tanx}\:\:{da}={sec}^{\mathrm{2}} {xdx} \\ $$$$\int\frac{{a}^{\mathrm{2}} {da}}{\:\sqrt{\mathrm{2}+\mathrm{1}+{a}^{\mathrm{2}} }} \\ $$$$\int\frac{{a}^{\mathrm{2}} +\mathrm{3}−\mathrm{3}}{\:\sqrt{{a}^{\mathrm{2}} +\mathrm{3}}}{da} \\ $$$$\int\sqrt{{a}^{\mathrm{2}} +\mathrm{3}}\:{da}−\mathrm{3}\int\frac{{da}}{\:\sqrt{{a}^{\mathrm{2}} +\mathrm{3}}} \\ $$$${now}\:{use}\:{formula} \\ $$$$\frac{{a}}{\mathrm{2}}\sqrt{{a}^{\mathrm{2}} +\mathrm{3}}\:+\frac{\mathrm{3}}{\mathrm{2}}{ln}\left({a}+\sqrt{{a}^{\mathrm{2}} +\mathrm{3}}\:\right)−\mathrm{3}{ln}\left({a}+\sqrt{{a}^{\mathrm{2}} +\mathrm{3}}\:\right)+{c} \\ $$$$\frac{{tanx}}{\mathrm{2}}\sqrt{{tan}^{\mathrm{2}} {x}+\mathrm{3}}\:−\frac{\mathrm{3}}{\mathrm{2}}{ln}\left({tanx}+\sqrt{{tan}^{\mathrm{2}} {x}+\mathrm{3}}\:\right)+{c} \\ $$
Answered by MJS last updated on 08/Feb/19
![let′s be cheeky ∫((sec^2 x tan^2 x)/( (√(2+sec^2 x))))dx= [t=(√(2+sec^2 x)) → x=arccos((1/( (√(t^2 −2))))); dx=((sec^2 x (√(2+sec^2 x)))/(tan x))dt] =∫tan x dt=∫(√(t^2 −3))dt= [u=((√3)/3)t → dt=(√3)du] =3∫(√(u^2 −1))du= [v=arcosh u → du=sinh v dv] =3∫sinh^2 v dv=(3/2)(v+sinh v cosh v)= =(3/2)(u(√(u^2 −1))−arcosh u)= =(1/2)(t(√(t^2 −3))−3arcosh ((t(√3))/3))= =(1/2)(√(sec^4 x +sec^2 x −2))−(3/2)arcosh (√((2+sec^2 x)/3)) +C](https://www.tinkutara.com/question/Q54634.png)
$$\mathrm{let}'\mathrm{s}\:\mathrm{be}\:\mathrm{cheeky} \\ $$$$\int\frac{\mathrm{sec}^{\mathrm{2}} \:{x}\:\mathrm{tan}^{\mathrm{2}} \:{x}}{\:\sqrt{\mathrm{2}+\mathrm{sec}^{\mathrm{2}} \:{x}}}{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\sqrt{\mathrm{2}+\mathrm{sec}^{\mathrm{2}} \:{x}}\:\rightarrow\:{x}=\mathrm{arccos}\left(\frac{\mathrm{1}}{\:\sqrt{{t}^{\mathrm{2}} −\mathrm{2}}}\right);\:{dx}=\frac{\mathrm{sec}^{\mathrm{2}} \:{x}\:\sqrt{\mathrm{2}+\mathrm{sec}^{\mathrm{2}} \:{x}}}{\mathrm{tan}\:{x}}{dt}\right] \\ $$$$=\int\mathrm{tan}\:{x}\:{dt}=\int\sqrt{{t}^{\mathrm{2}} −\mathrm{3}}{dt}= \\ $$$$\:\:\:\:\:\left[{u}=\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}{t}\:\rightarrow\:{dt}=\sqrt{\mathrm{3}}{du}\right] \\ $$$$=\mathrm{3}\int\sqrt{{u}^{\mathrm{2}} −\mathrm{1}}{du}= \\ $$$$\:\:\:\:\:\left[{v}=\mathrm{arcosh}\:{u}\:\rightarrow\:{du}=\mathrm{sinh}\:{v}\:{dv}\right] \\ $$$$=\mathrm{3}\int\mathrm{sinh}^{\mathrm{2}} \:{v}\:{dv}=\frac{\mathrm{3}}{\mathrm{2}}\left({v}+\mathrm{sinh}\:{v}\:\mathrm{cosh}\:{v}\right)= \\ $$$$=\frac{\mathrm{3}}{\mathrm{2}}\left({u}\sqrt{{u}^{\mathrm{2}} −\mathrm{1}}−\mathrm{arcosh}\:{u}\right)= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left({t}\sqrt{{t}^{\mathrm{2}} −\mathrm{3}}−\mathrm{3arcosh}\:\frac{{t}\sqrt{\mathrm{3}}}{\mathrm{3}}\right)= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\mathrm{sec}^{\mathrm{4}} \:{x}\:+\mathrm{sec}^{\mathrm{2}} \:{x}\:−\mathrm{2}}−\frac{\mathrm{3}}{\mathrm{2}}\mathrm{arcosh}\:\sqrt{\frac{\mathrm{2}+\mathrm{sec}^{\mathrm{2}} \:{x}}{\mathrm{3}}}\:+{C} \\ $$
