Question Number 54679 by Raj Singh last updated on 09/Feb/19

Commented by maxmathsup by imad last updated on 09/Feb/19
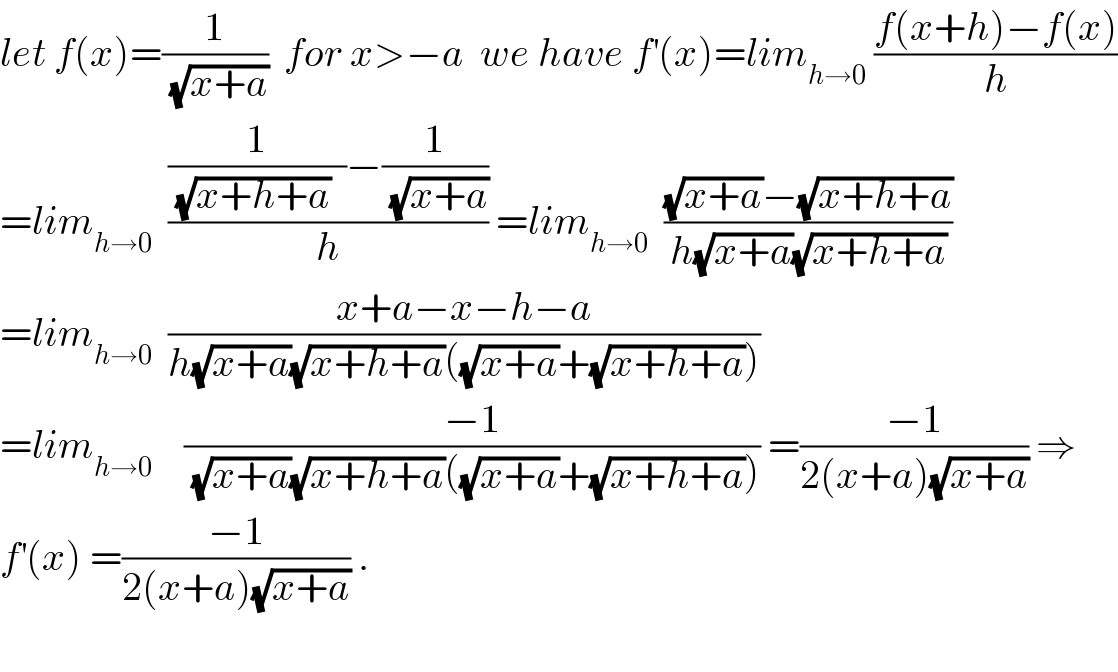
$${let}\:{f}\left({x}\right)=\frac{\mathrm{1}}{\:\sqrt{{x}+{a}}}\:\:{for}\:{x}>−{a}\:\:{we}\:{have}\:{f}^{'} \left({x}\right)={lim}_{{h}\rightarrow\mathrm{0}} \:\frac{{f}\left({x}+{h}\right)−{f}\left({x}\right)}{{h}} \\ $$$$={lim}_{{h}\rightarrow\mathrm{0}} \:\:\frac{\frac{\mathrm{1}}{\:\sqrt{{x}+{h}+{a}}\:\:}−\frac{\mathrm{1}}{\:\sqrt{{x}+{a}}}}{{h}}\:={lim}_{{h}\rightarrow\mathrm{0}} \:\:\frac{\sqrt{{x}+{a}}−\sqrt{{x}+{h}+{a}}}{{h}\sqrt{{x}+{a}}\sqrt{{x}+{h}+{a}}} \\ $$$$={lim}_{{h}\rightarrow\mathrm{0}} \:\:\frac{{x}+{a}−{x}−{h}−{a}}{{h}\sqrt{{x}+{a}}\sqrt{{x}+{h}+{a}}\left(\sqrt{{x}+{a}}+\sqrt{{x}+{h}+{a}}\right)} \\ $$$$={lim}_{{h}\rightarrow\mathrm{0}} \:\:\:\:\frac{−\mathrm{1}}{\:\sqrt{{x}+{a}}\sqrt{{x}+{h}+{a}}\left(\sqrt{{x}+{a}}+\sqrt{{x}+{h}+{a}}\right)}\:=\frac{−\mathrm{1}}{\mathrm{2}\left({x}+{a}\right)\sqrt{{x}+{a}}}\:\Rightarrow \\ $$$${f}^{'} \left({x}\right)\:=\frac{−\mathrm{1}}{\mathrm{2}\left({x}+{a}\right)\sqrt{{x}+{a}}}\:. \\ $$$$ \\ $$
Answered by kaivan.ahmadi last updated on 09/Feb/19
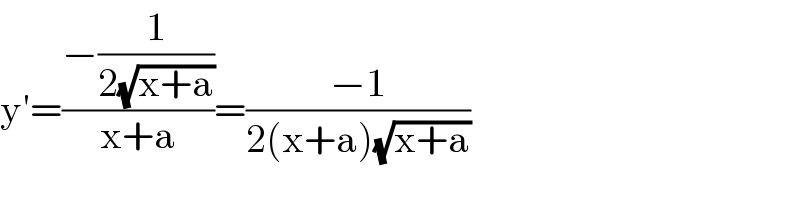
$$\mathrm{y}'=\frac{−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{x}+\mathrm{a}}}}{\mathrm{x}+\mathrm{a}}=\frac{−\mathrm{1}}{\mathrm{2}\left(\mathrm{x}+\mathrm{a}\right)\sqrt{\mathrm{x}+\mathrm{a}}} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 09/Feb/19

$${y}=\frac{\mathrm{1}}{\:\sqrt{{x}+{a}}} \\ $$$${y}+\bigtriangleup{y}=\frac{\mathrm{1}}{\:\sqrt{{x}+\bigtriangleup{x}+{a}}} \\ $$$$\bigtriangleup{y}=\frac{\mathrm{1}}{\:\sqrt{{x}+\bigtriangleup{x}+{a}}}−\frac{\mathrm{1}}{\:\sqrt{{x}+{a}}} \\ $$$$\bigtriangleup{y}=\frac{\sqrt{{x}+{a}}\:−\sqrt{{x}+\bigtriangleup{x}+{a}}}{\:\sqrt{{x}+{a}}\:×\sqrt{{x}+\bigtriangleup{x}+{a}}\:} \\ $$$$\bigtriangleup{y}=\frac{\left({x}+{a}\right)−\left({x}+\bigtriangleup{x}+{a}\right)}{\left\{\sqrt{{x}+{a}}\:×\sqrt{{x}+\bigtriangleup{x}+{a}}\:\right\}\left\{\sqrt{{x}+{a}}\:+\sqrt{{x}+\bigtriangleup{x}+{a}}\:\right\}} \\ $$$$\frac{\bigtriangleup{y}}{\bigtriangleup{x}}=\frac{−\mathrm{1}}{\left\{\sqrt{{x}+{a}}\:×\sqrt{{x}+\bigtriangleup{x}+{a}}\:\right\}\left\{\sqrt{{x}+{a}}\:+\sqrt{{x}+\bigtriangleup{x}+{a}}\:\right\}} \\ $$$$\frac{{dy}}{{dx}}=\underset{\bigtriangleup{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\bigtriangleup{y}}{\bigtriangleup{x}} \\ $$$${so}\:{answer}\:{is} \\ $$$$\frac{{dy}}{{dx}}=\frac{−\mathrm{1}}{\left\{\sqrt{{x}+{a}}\:×\sqrt{{x}+{a}}\:\right\}\left\{\sqrt{{x}+{a}}\:+\sqrt{{x}+{a}}\:\right\}} \\ $$$$\frac{{dy}}{{dx}}=\frac{−\mathrm{1}}{\mathrm{2}\left({x}+{a}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} } \\ $$
