Menu Close

Question-54701

Tinku Tara 0 Comments
Pin




Question Number 54701 by Meritguide1234 last updated on 09/Feb/19
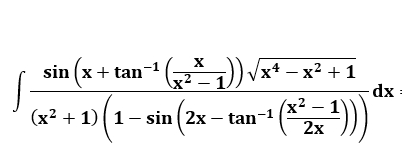
Answered by behi83417@gmail.com last updated on 09/Feb/19
tg^(−1) (x/(x^2 −1))=a sin^2 a=(1/(1+cot^2 a))=(1/(1+x^2 +x^(−2) −2))=(x^2 /(x^4 −x^2 +1)) ⇒(√(x^4 −x^2 +1))=(x/(sina)) cos^2 a=(1/(1+tg^2 a))=(1/(1+(x^2 /((x^2 −1)^2 ))))=(((x^2 −1)^2 )/(x^4 −x^2 +1)) ⇒cosa=((x^2 −1)/( (√(x^4 −x^2 +1)))) sin(x+a)=sinx.((x^2 −1)/( (√(x^4 −x^2 +1))))+cosx.(x/( (√(x^4 −x^2 +1)))) tg^(−1) ((x^2 −1)/(2x))=b⇒cos^2 b=(1/(1+(((x^2 −1)^2 )/(4x^2 ))))⇒ cosb=((2x)/(x^2 +1)),sinb=((x^2 −1)/(x^2 +1)) sin(2x−b)=sin2x.((2x)/(x^2 +1))−cos2x.((x^2 −1)/(x^2 +1)) ⇒I=∫(((x^2 −1).sinx+x.cosx)/([(x^2 +1)+(x^2 −1)cos2x−2xsin2x]))dx
$${tg}^{−\mathrm{1}} \frac{{x}}{{x}^{\mathrm{2}} −\mathrm{1}}={a} \\ $$$${sin}^{\mathrm{2}} {a}=\frac{\mathrm{1}}{\mathrm{1}+{cot}^{\mathrm{2}} {a}}=\frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} +{x}^{−\mathrm{2}} −\mathrm{2}}=\frac{{x}^{\mathrm{2}} }{{x}^{\mathrm{4}} −{x}^{\mathrm{2}} +\mathrm{1}} \\ $$$$\Rightarrow\sqrt{{x}^{\mathrm{4}} −{x}^{\mathrm{2}} +\mathrm{1}}=\frac{{x}}{{sina}} \\ $$$${cos}^{\mathrm{2}} {a}=\frac{\mathrm{1}}{\mathrm{1}+{tg}^{\mathrm{2}} {a}}=\frac{\mathrm{1}}{\mathrm{1}+\frac{{x}^{\mathrm{2}} }{\left({x}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} }}=\frac{\left({x}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} }{{x}^{\mathrm{4}} −{x}^{\mathrm{2}} +\mathrm{1}} \\ $$$$\Rightarrow{cosa}=\frac{{x}^{\mathrm{2}} −\mathrm{1}}{\:\sqrt{{x}^{\mathrm{4}} −{x}^{\mathrm{2}} +\mathrm{1}}} \\ $$$${sin}\left({x}+{a}\right)={sinx}.\frac{{x}^{\mathrm{2}} −\mathrm{1}}{\:\sqrt{{x}^{\mathrm{4}} −{x}^{\mathrm{2}} +\mathrm{1}}}+{cosx}.\frac{{x}}{\:\sqrt{{x}^{\mathrm{4}} −{x}^{\mathrm{2}} +\mathrm{1}}} \\ $$$${tg}^{−\mathrm{1}} \frac{{x}^{\mathrm{2}} −\mathrm{1}}{\mathrm{2}{x}}={b}\Rightarrow{cos}^{\mathrm{2}} {b}=\frac{\mathrm{1}}{\mathrm{1}+\frac{\left({x}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{4}{x}^{\mathrm{2}} }}\Rightarrow \\ $$$${cosb}=\frac{\mathrm{2}{x}}{{x}^{\mathrm{2}} +\mathrm{1}},{sinb}=\frac{{x}^{\mathrm{2}} −\mathrm{1}}{{x}^{\mathrm{2}} +\mathrm{1}} \\ $$$${sin}\left(\mathrm{2}{x}−{b}\right)={sin}\mathrm{2}{x}.\frac{\mathrm{2}{x}}{{x}^{\mathrm{2}} +\mathrm{1}}−{cos}\mathrm{2}{x}.\frac{{x}^{\mathrm{2}} −\mathrm{1}}{{x}^{\mathrm{2}} +\mathrm{1}} \\ $$$$\Rightarrow{I}=\int\frac{\left({x}^{\mathrm{2}} −\mathrm{1}\right).{sinx}+{x}.{cosx}}{\left[\left({x}^{\mathrm{2}} +\mathrm{1}\right)+\left({x}^{\mathrm{2}} −\mathrm{1}\right){cos}\mathrm{2}{x}−\mathrm{2}{xsin}\mathrm{2}{x}\right]}{dx} \\ $$
Commented by Meritguide1234 last updated on 09/Feb/19
check again
$$\mathrm{check}\:\mathrm{again} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 10/Feb/19
tan^(−1) ((x/(x^2 −1))) sec^2 a=((x^4 −2x^2 +1+x^2 )/((x^2 −1)^2 ))=((x^4 −x^2 +1)/((x^2 −1)^2 )) cos^2 a=(((x^2 −1)^2 )/(x^4 −x^2 +1)) cosa=((x^2 −1)/( (√(x^4 −x^2 +1)))) sin^2 a=1−(((x^4 −2x^2 +1))/(x^4 −x^2 +1))=((x^4 −x^2 +1−x^4 +2x^2 −1)/(x^4 −x^2 +1)) sina=(x/( (√(x^4 −x^2 +1)))) so sin(x+tan^(−1) (x/(x^2 −1)))=sinx×((x^2 −1)/( (√(x^4 −x^2 +1))))+cosx×(x/( (√(x^4 −x^2 +1)))) so N_r ={(x^2 −1)sinx+xcosx}×(1/( (√(x^4 −x^2 +1))))×(√(x^4 −x^2 +1)) N_r =(x^2 −1)sinx+xcosx ★tanb=((x^2 −1)/(2x)) sec^2 b=1+((x^4 −2x^2 +1)/(4x^2 ))=(((x^2 +1)^2 )/((2x)^2 )) cosb=((2x)/((x^2 +1))) sin^2 b=(((x^2 +1)^2 −4x^2 )/((x^2 +1)^2 ))=(((x^2 −1)/(x^2 +1)))^2 sinb=((x^2 −1)/(x^2 +1)) or ((1−x^2 )/(1+x^2 )) sin(2x−tan^(−1) ((x^2 −1)/(2x))) =sin2x×((2x)/(x^2 +1))−co2x×((x^2 −1)/(x^2 +1)) or sin2x×((2x)/(x^2 +1))−cos2x×((1−x^2 )/(1+x^2 )) ((2xsin2x−(x^2 −1)cos2x)/(x^2 +1)) =(((2xsin2x−(x^2 −1)cos2x)/(x^2 +1)) ((2xsin2x−(1−x^2 )cos2x)/(x^2 +1)) so D_r =(x^2 +1){1−((2xsin2x−(x^2 −1)cos2x)/(x^2 +1))} =x^2 +1−2xsin2x+(x^2 −1)cos2x =x^2 +1−4xsinxcosx+x^2 cos2x−cos2x =x^2 (1+cos2x)+1−cos2x−4xsinxcosx =2x^2 cos^2 x+2sin^2 x−4xsinxcosx =2(xcosx−sinx)^2 or2(sinx−xcosx)^2 or D_r =(x^2 +1){1−((2xsin2x−(1−x^2 )cos2x)/(x^2 +1))} =x^2 +1−2xsin2x+(1−x^2 )cos2x =x^2 +1−4xsinxcosx+cos2x−x^2 cos2x =x^2 (1−cos2x)+1+cos2x−4xsinxcosx =2x^2 sin^2 x+2cos^2 x−4xsinxcosx =2(xsinx−cosx)^2 or2(cosx−xsinx)^2 I_(blue) =∫(((x^2 −1)sinx+xcosx)/(2(xcosx−sinx)^2 ))dx.....1 or ∫(((x^2 −1)sinx+xcosx)/(2(sinx−xcosx)^2 ))dx.......2 I_(red) =∫(((x^2 −1)sinx+xcosx)/(2(xsinx−cosx)^2 ))dx.....3 or∫(((x^2 −1)sinx+xcosx)/(2(cosx−xsinx)^2 ))dx....4 four intregation... (d/dx)(xcosx−sinx)=−xsinx+cosx−cosx=−xsinx (d/dx)(sinx−xcosx)=cosx−(x×−sinx+cosx)=xsinx (1/2)∫(/) (d/(dx ))(xsinx−cosx)=xcosx+sinx+sinx=xcosx+2sinx (d/dx)(cosx−xsinx)=−sinx−xcosx−sinx=−(xcosx+2sinx)
$$ \\ $$$${tan}^{−\mathrm{1}} \left(\frac{{x}}{{x}^{\mathrm{2}} −\mathrm{1}}\right) \\ $$$${sec}^{\mathrm{2}} {a}=\frac{{x}^{\mathrm{4}} −\mathrm{2}{x}^{\mathrm{2}} +\mathrm{1}+{x}^{\mathrm{2}} }{\left({x}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} }=\frac{{x}^{\mathrm{4}} −{x}^{\mathrm{2}} +\mathrm{1}}{\left({x}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} } \\ $$$${cos}^{\mathrm{2}} {a}=\frac{\left({x}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} }{{x}^{\mathrm{4}} −{x}^{\mathrm{2}} +\mathrm{1}}\:{cosa}=\frac{{x}^{\mathrm{2}} −\mathrm{1}}{\:\sqrt{{x}^{\mathrm{4}} −{x}^{\mathrm{2}} +\mathrm{1}}} \\ $$$${sin}^{\mathrm{2}} {a}=\mathrm{1}−\frac{\left({x}^{\mathrm{4}} −\mathrm{2}{x}^{\mathrm{2}} +\mathrm{1}\right)}{{x}^{\mathrm{4}} −{x}^{\mathrm{2}} +\mathrm{1}}=\frac{{x}^{\mathrm{4}} −{x}^{\mathrm{2}} +\mathrm{1}−{x}^{\mathrm{4}} +\mathrm{2}{x}^{\mathrm{2}} −\mathrm{1}}{{x}^{\mathrm{4}} −{x}^{\mathrm{2}} +\mathrm{1}} \\ $$$${sina}=\frac{{x}}{\:\sqrt{{x}^{\mathrm{4}} −{x}^{\mathrm{2}} +\mathrm{1}}} \\ $$$${so}\:{sin}\left({x}+{tan}^{−\mathrm{1}} \frac{{x}}{{x}^{\mathrm{2}} −\mathrm{1}}\right)={sinx}×\frac{{x}^{\mathrm{2}} −\mathrm{1}}{\:\sqrt{{x}^{\mathrm{4}} −{x}^{\mathrm{2}} +\mathrm{1}}}+{cosx}×\frac{{x}}{\:\sqrt{{x}^{\mathrm{4}} −{x}^{\mathrm{2}} +\mathrm{1}}} \\ $$$${so}\:{N}_{{r}} =\left\{\left({x}^{\mathrm{2}} −\mathrm{1}\right){sinx}+{xcosx}\right\}×\frac{\mathrm{1}}{\:\sqrt{{x}^{\mathrm{4}} −{x}^{\mathrm{2}} +\mathrm{1}}}×\sqrt{{x}^{\mathrm{4}} −{x}^{\mathrm{2}} +\mathrm{1}} \\ $$$$\boldsymbol{{N}}_{{r}} =\left({x}^{\mathrm{2}} −\mathrm{1}\right){sinx}+{xcosx} \\ $$$$\bigstar{tanb}=\frac{{x}^{\mathrm{2}} −\mathrm{1}}{\mathrm{2}{x}}\:\:{sec}^{\mathrm{2}} {b}=\mathrm{1}+\frac{{x}^{\mathrm{4}} −\mathrm{2}{x}^{\mathrm{2}} +\mathrm{1}}{\mathrm{4}{x}^{\mathrm{2}} }=\frac{\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }{\left(\mathrm{2}{x}\right)^{\mathrm{2}} } \\ $$$${cosb}=\frac{\mathrm{2}{x}}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)}\:\:{sin}^{\mathrm{2}} {b}=\frac{\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} −\mathrm{4}{x}^{\mathrm{2}} }{\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }=\left(\frac{{x}^{\mathrm{2}} −\mathrm{1}}{{x}^{\mathrm{2}} +\mathrm{1}}\right)^{\mathrm{2}} \\ $$$${sinb}=\frac{{x}^{\mathrm{2}} −\mathrm{1}}{{x}^{\mathrm{2}} +\mathrm{1}}\:{or}\:\frac{\mathrm{1}−{x}^{\mathrm{2}} }{\mathrm{1}+{x}^{\mathrm{2}} } \\ $$$${sin}\left(\mathrm{2}{x}−{tan}^{−\mathrm{1}} \frac{{x}^{\mathrm{2}} −\mathrm{1}}{\mathrm{2}{x}}\right) \\ $$$$={sin}\mathrm{2}{x}×\frac{\mathrm{2}{x}}{{x}^{\mathrm{2}} +\mathrm{1}}−{co}\mathrm{2}{x}×\frac{{x}^{\mathrm{2}} −\mathrm{1}}{{x}^{\mathrm{2}} +\mathrm{1}} \\ $$$${or}\:{sin}\mathrm{2}{x}×\frac{\mathrm{2}{x}}{{x}^{\mathrm{2}} +\mathrm{1}}−{cos}\mathrm{2}{x}×\frac{\mathrm{1}−{x}^{\mathrm{2}} }{\mathrm{1}+{x}^{\mathrm{2}} } \\ $$$$\frac{\mathrm{2}{xsin}\mathrm{2}{x}−\left({x}^{\mathrm{2}} −\mathrm{1}\right){cos}\mathrm{2}{x}}{{x}^{\mathrm{2}} +\mathrm{1}} \\ $$$$=\frac{\left(\mathrm{2}{xsin}\mathrm{2}{x}−\left({x}^{\mathrm{2}} −\mathrm{1}\right){cos}\mathrm{2}{x}\right.}{{x}^{\mathrm{2}} +\mathrm{1}} \\ $$$$\frac{\mathrm{2}{xsin}\mathrm{2}{x}−\left(\mathrm{1}−{x}^{\mathrm{2}} \right){cos}\mathrm{2}{x}}{{x}^{\mathrm{2}} +\mathrm{1}} \\ $$$$\boldsymbol{{so}}\:\boldsymbol{{D}}_{{r}} =\left({x}^{\mathrm{2}} +\mathrm{1}\right)\left\{\mathrm{1}−\frac{\mathrm{2}{xsin}\mathrm{2}{x}−\left({x}^{\mathrm{2}} −\mathrm{1}\right){cos}\mathrm{2}{x}}{{x}^{\mathrm{2}} +\mathrm{1}}\right\} \\ $$$$={x}^{\mathrm{2}} +\mathrm{1}−\mathrm{2}{xsin}\mathrm{2}{x}+\left({x}^{\mathrm{2}} −\mathrm{1}\right){cos}\mathrm{2}{x} \\ $$$$={x}^{\mathrm{2}} +\mathrm{1}−\mathrm{4}{xsinxcosx}+{x}^{\mathrm{2}} {cos}\mathrm{2}{x}−{cos}\mathrm{2}{x} \\ $$$$={x}^{\mathrm{2}} \left(\mathrm{1}+{cos}\mathrm{2}{x}\right)+\mathrm{1}−{cos}\mathrm{2}{x}−\mathrm{4}{xsinxcosx} \\ $$$$=\mathrm{2}{x}^{\mathrm{2}} {cos}^{\mathrm{2}} {x}+\mathrm{2}{sin}^{\mathrm{2}} {x}−\mathrm{4}{xsinxcosx} \\ $$$$=\mathrm{2}\left({xcosx}−{sinx}\right)^{\mathrm{2}} \:{or}\mathrm{2}\left({sinx}−{xcosx}\right)^{\mathrm{2}} \\ $$$$ \\ $$$${or}\:{D}_{{r}} =\left({x}^{\mathrm{2}} +\mathrm{1}\right)\left\{\mathrm{1}−\frac{\mathrm{2}{xsin}\mathrm{2}{x}−\left(\mathrm{1}−{x}^{\mathrm{2}} \right){cos}\mathrm{2}{x}}{{x}^{\mathrm{2}} +\mathrm{1}}\right\} \\ $$$$={x}^{\mathrm{2}} +\mathrm{1}−\mathrm{2}{xsin}\mathrm{2}{x}+\left(\mathrm{1}−{x}^{\mathrm{2}} \right){cos}\mathrm{2}{x} \\ $$$$={x}^{\mathrm{2}} +\mathrm{1}−\mathrm{4}{xsinxcosx}+{cos}\mathrm{2}{x}−{x}^{\mathrm{2}} {cos}\mathrm{2}{x} \\ $$$$={x}^{\mathrm{2}} \left(\mathrm{1}−{cos}\mathrm{2}{x}\right)+\mathrm{1}+{cos}\mathrm{2}{x}−\mathrm{4}{xsinxcosx} \\ $$$$=\mathrm{2}{x}^{\mathrm{2}} {sin}^{\mathrm{2}} {x}+\mathrm{2}{cos}^{\mathrm{2}} {x}−\mathrm{4}{xsinxcosx} \\ $$$$=\mathrm{2}\left({xsinx}−{cosx}\right)^{\mathrm{2}} \:{or}\mathrm{2}\left({cosx}−{xsinx}\right)^{\mathrm{2}} \\ $$$${I}_{{blue}} =\int\frac{\left({x}^{\mathrm{2}} −\mathrm{1}\right){sinx}+{xcosx}}{\mathrm{2}\left({xcosx}−{sinx}\right)^{\mathrm{2}} }{dx}…..\mathrm{1} \\ $$$${or}\:\int\frac{\left({x}^{\mathrm{2}} −\mathrm{1}\right){sinx}+{xcosx}}{\mathrm{2}\left({sinx}−{xcosx}\right)^{\mathrm{2}} }{dx}…….\mathrm{2} \\ $$$${I}_{{red}} =\int\frac{\left({x}^{\mathrm{2}} −\mathrm{1}\right){sinx}+{xcosx}}{\mathrm{2}\left({xsinx}−{cosx}\right)^{\mathrm{2}} }{dx}…..\mathrm{3} \\ $$$${or}\int\frac{\left({x}^{\mathrm{2}} −\mathrm{1}\right){sinx}+{xcosx}}{\mathrm{2}\left({cosx}−{xsinx}\right)^{\mathrm{2}} }{dx}….\mathrm{4} \\ $$$${four}\:{intregation}… \\ $$$$\frac{{d}}{{dx}}\left({xcosx}−{sinx}\right)=−{xsinx}+{cosx}−{cosx}=−{xsinx} \\ $$$$\frac{{d}}{{dx}}\left({sinx}−{xcosx}\right)={cosx}−\left({x}×−{sinx}+{cosx}\right)={xsinx} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int\frac{}{} \\ $$$$\frac{{d}}{{dx}\:}\left({xsinx}−{cosx}\right)={xcosx}+{sinx}+{sinx}={xcosx}+\mathrm{2}{sinx} \\ $$$$\frac{{d}}{{dx}}\left({cosx}−{xsinx}\right)=−{sinx}−{xcosx}−{sinx}=−\left({xcosx}+\mathrm{2}{sinx}\right) \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 09/Feb/19
i will try to solve in copy then upload it...
$${i}\:{will}\:{try}\:{to}\:{solve}\:{in}\:{copy}\:{then}\:{upload}\:{it}… \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *