Question Number 54856 by Meritguide1234 last updated on 13/Feb/19
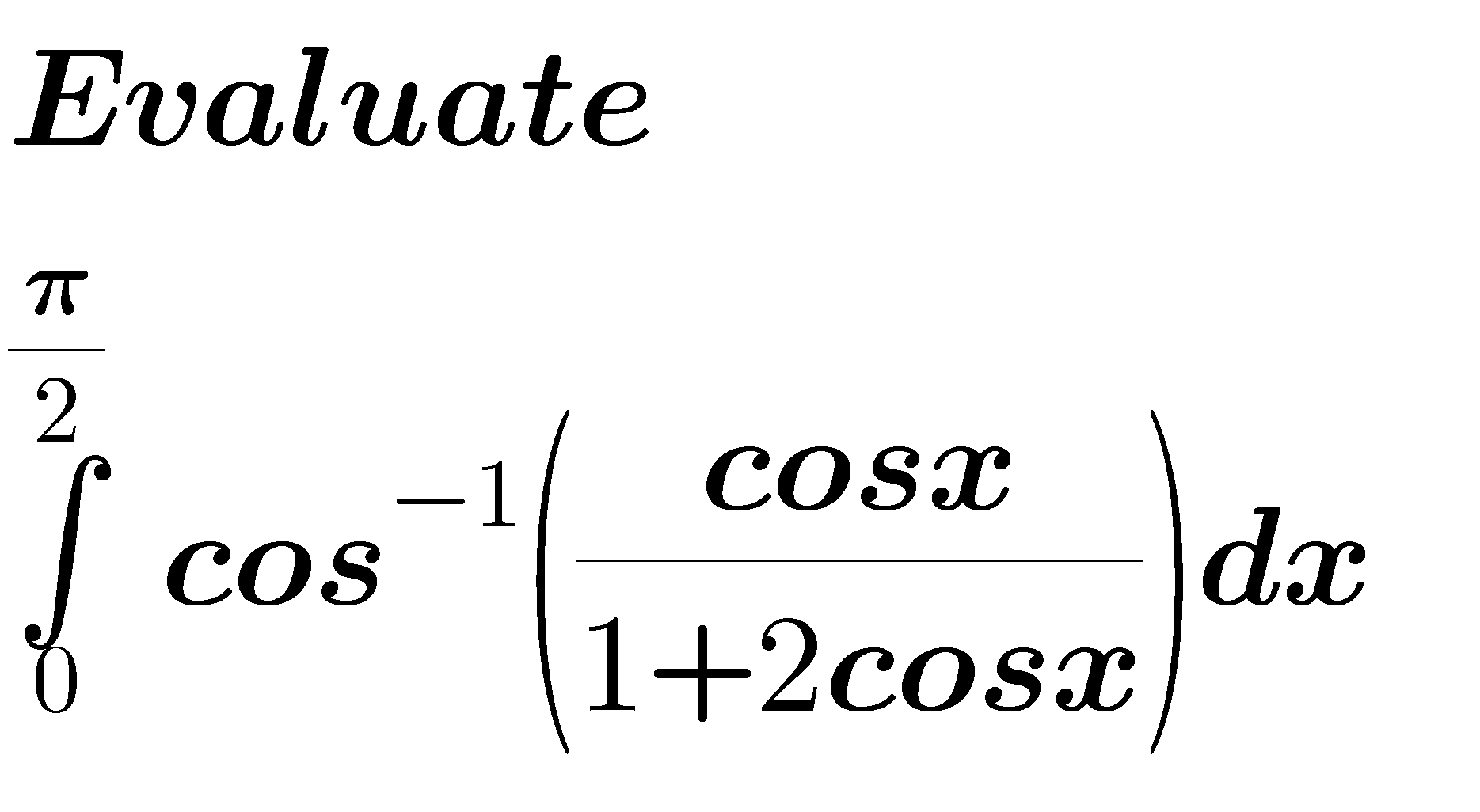
Commented by Meritguide1234 last updated on 14/Feb/19
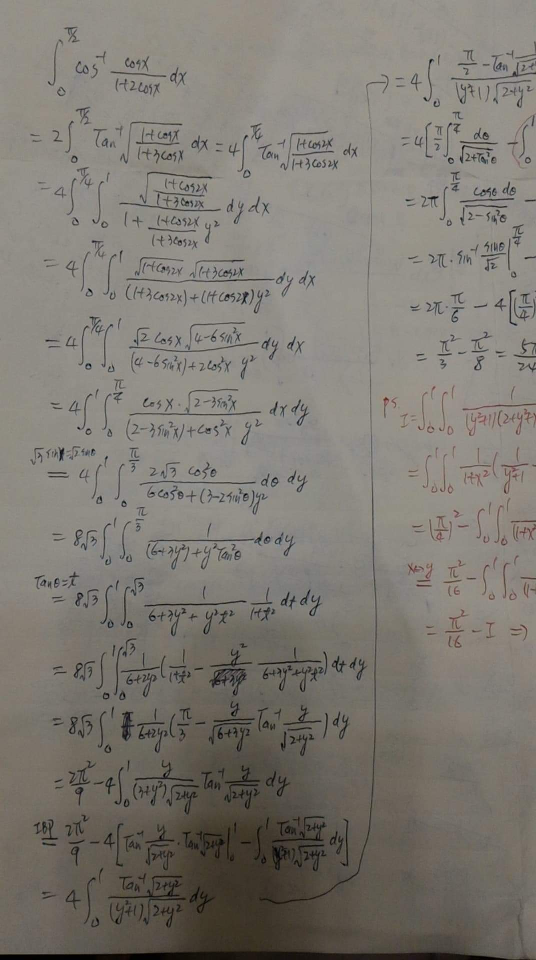
Commented by Meritguide1234 last updated on 14/Feb/19
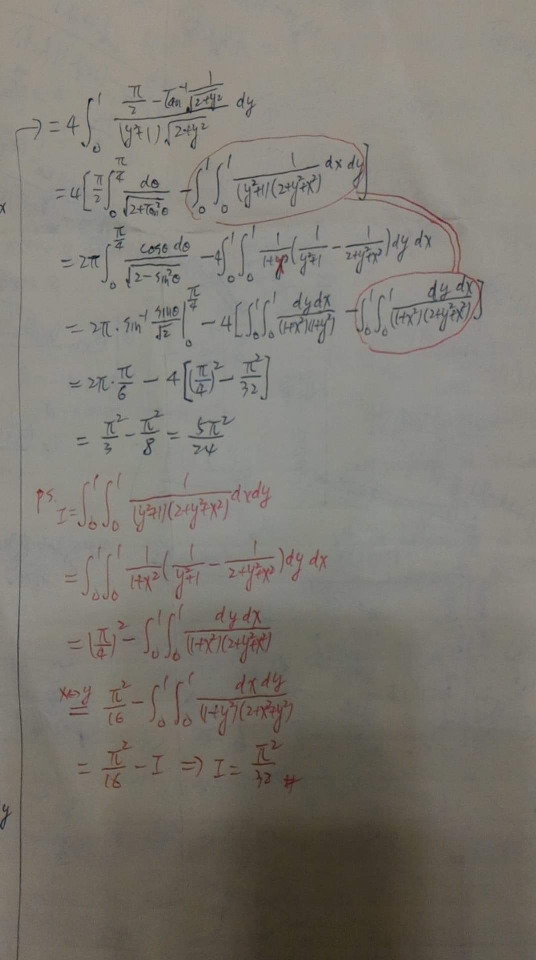
Answered by tanmay.chaudhury50@gmail.com last updated on 13/Feb/19

$$\frac{{cosx}}{\mathrm{1}+\mathrm{2}{cosx}} \\ $$$$\frac{\frac{\mathrm{1}}{\mathrm{2}}{cosx}}{\frac{\mathrm{1}}{\mathrm{2}}+{cosx}}\rightarrow\frac{{cos}\frac{\pi}{\mathrm{3}}{cosx}}{{cos}\frac{\pi}{\mathrm{3}}+{cosx}}\rightarrow\frac{{ab}}{{a}+{b}}\rightarrow\frac{{ab}}{\left(\sqrt{{a}}\:−\sqrt{{b}}\:\right)^{\mathrm{2}} +\mathrm{2}\sqrt{{a}}\:\sqrt{{b}}\:} \\ $$$${max}\:{value}\:{of}\:\frac{{ab}}{{a}+{b}}\:{when}\:{D}_{{r}} ={min}\:\rightarrow\:\sqrt{{a}}\:−\sqrt{{b}}\:=\mathrm{0} \\ $$$${cosx}={cos}\frac{\pi}{\mathrm{3}}\rightarrow{x}=\frac{\pi}{\mathrm{3}} \\ $$$${cos}^{−\mathrm{1}} \left(\frac{{cosx}}{\mathrm{1}+\mathrm{2}{cosx}}\right)\rightarrow{cos}^{−\mathrm{1}} \left(\frac{\frac{\mathrm{1}}{\mathrm{2}}}{\mathrm{1}+\mathrm{2}×\frac{\mathrm{1}}{\mathrm{2}}}\right)\rightarrow{cos}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{4}}\right) \\ $$$${cos}^{−\mathrm{1}} \left(\frac{{cosx}}{\mathrm{1}+\mathrm{2}{cosx}}\right)\rightarrow{cos}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{1}+\mathrm{2}×\mathrm{1}}\right)\:{atx}=\mathrm{0} \\ $$$${cos}^{−\mathrm{1}} \left(\frac{{cos}\frac{\pi}{\mathrm{2}}}{\mathrm{1}+\mathrm{2}{cos}\frac{\pi}{\mathrm{2}\:}}\right)\rightarrow{cos}^{−\mathrm{1}} \left(\mathrm{0}\right)\:{at}\:{x}=\frac{\pi}{\mathrm{2}}\: \\ $$$$\:{cos}^{−} \left(\mathrm{0}\right)\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {dx}>\:{cos}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{4}}\right)\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {dx}>\:{cos}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{3}}\right)\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {dx} \\ $$$${so}\:\frac{\pi}{\mathrm{2}}×\frac{\pi}{\mathrm{2}}>{I}>{cos}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{3}}\right)×\frac{\pi}{\mathrm{2}} \\ $$$${pls}\:{check}… \\ $$
Commented by Meritguide1234 last updated on 13/Feb/19
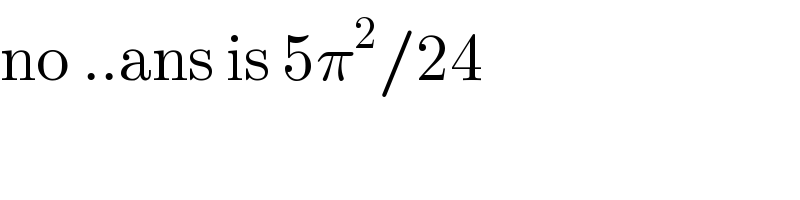
$$\mathrm{no}\:..\mathrm{ans}\:\mathrm{is}\:\mathrm{5}\pi^{\mathrm{2}} /\mathrm{24} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 14/Feb/19
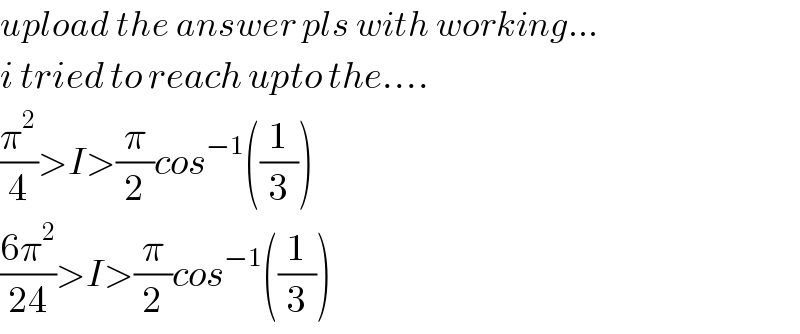
$${upload}\:{the}\:{answer}\:{pls}\:{with}\:{working}… \\ $$$${i}\:{tried}\:{to}\:{reach}\:{upto}\:{the}…. \\ $$$$\frac{\pi^{\mathrm{2}} }{\mathrm{4}}>{I}>\frac{\pi}{\mathrm{2}}{cos}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{3}}\right) \\ $$$$\frac{\mathrm{6}\pi^{\mathrm{2}} }{\mathrm{24}}>{I}>\frac{\pi}{\mathrm{2}}{cos}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{3}}\right) \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 14/Feb/19
$${thsnk}\:{you}\:{sir}…{let}\:{me}\:{unlock}\:{the}\:{secret}… \\ $$
