Question Number 54860 by Tinkutara last updated on 13/Feb/19
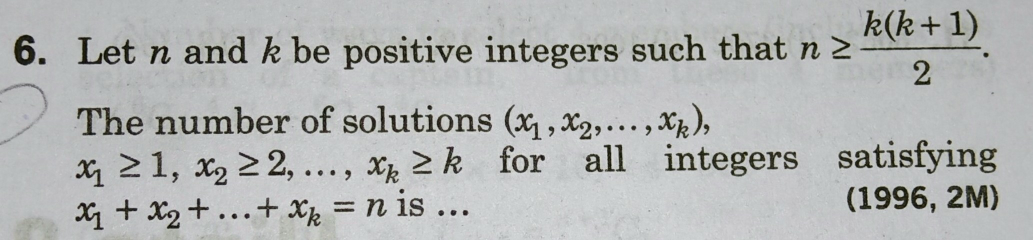
Commented by Tinkutara last updated on 14/Feb/19

$${But}\:{answer}\:{is} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{2}{n}−{k}^{\mathrm{2}} +{k}−\mathrm{2}\right) \\ $$
Answered by kaivan.ahmadi last updated on 14/Feb/19
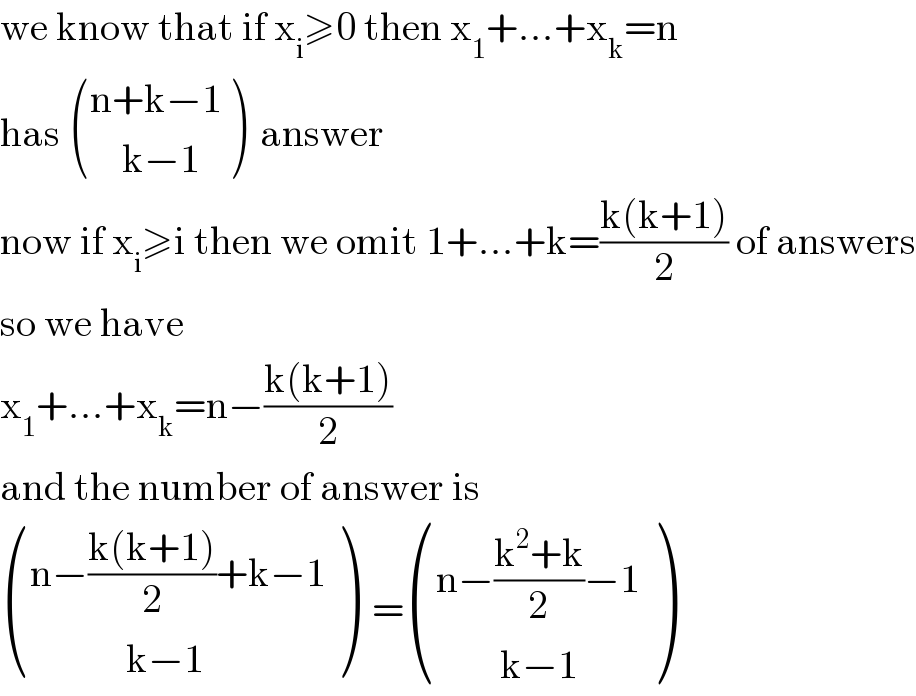
$$\mathrm{we}\:\mathrm{know}\:\mathrm{that}\:\mathrm{if}\:\mathrm{x}_{\mathrm{i}} \geqslant\mathrm{0}\:\mathrm{then}\:\mathrm{x}_{\mathrm{1}} +…+\mathrm{x}_{\mathrm{k}} =\mathrm{n} \\ $$$$\mathrm{has}\:\begin{pmatrix}{\mathrm{n}+\mathrm{k}−\mathrm{1}}\\{\:\:\:\:\mathrm{k}−\mathrm{1}}\end{pmatrix}\:\:\mathrm{answer} \\ $$$$\mathrm{now}\:\mathrm{if}\:\mathrm{x}_{\mathrm{i}} \geqslant\mathrm{i}\:\mathrm{then}\:\mathrm{we}\:\mathrm{omit}\:\mathrm{1}+…+\mathrm{k}=\frac{\mathrm{k}\left(\mathrm{k}+\mathrm{1}\right)}{\mathrm{2}}\:\mathrm{of}\:\mathrm{answers} \\ $$$$\mathrm{so}\:\mathrm{we}\:\mathrm{have} \\ $$$$\mathrm{x}_{\mathrm{1}} +…+\mathrm{x}_{\mathrm{k}} =\mathrm{n}−\frac{\mathrm{k}\left(\mathrm{k}+\mathrm{1}\right)}{\mathrm{2}} \\ $$$$\mathrm{and}\:\mathrm{the}\:\mathrm{number}\:\mathrm{of}\:\mathrm{answer}\:\mathrm{is} \\ $$$$\begin{pmatrix}{\mathrm{n}−\frac{\mathrm{k}\left(\mathrm{k}+\mathrm{1}\right)}{\mathrm{2}}+\mathrm{k}−\mathrm{1}}\\{\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{k}−\mathrm{1}}\end{pmatrix}\:\:=\begin{pmatrix}{\mathrm{n}−\frac{\mathrm{k}^{\mathrm{2}} +\mathrm{k}}{\mathrm{2}}−\mathrm{1}}\\{\:\:\:\:\:\:\:\:\mathrm{k}−\mathrm{1}}\end{pmatrix} \\ $$
