Question Number 55129 by MJS last updated on 17/Feb/19
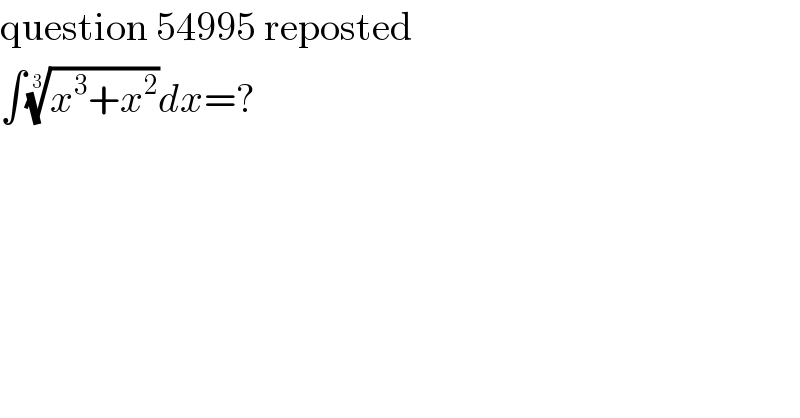
$$\mathrm{question}\:\mathrm{54995}\:\mathrm{reposted} \\ $$$$\int\sqrt[{\mathrm{3}}]{{x}^{\mathrm{3}} +{x}^{\mathrm{2}} }{dx}=? \\ $$
Commented by Meritguide1234 last updated on 18/Feb/19
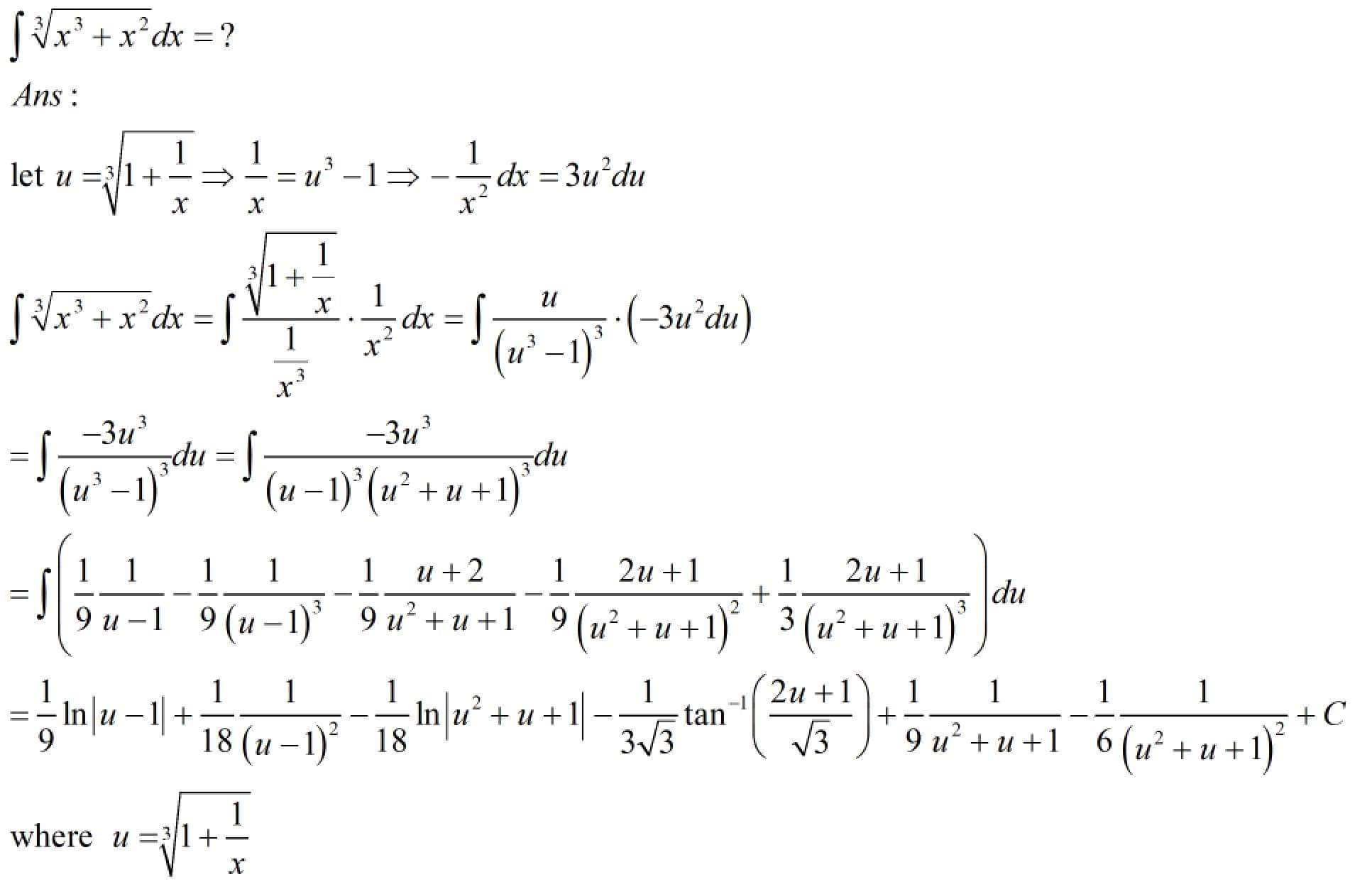
Answered by MJS last updated on 18/Feb/19
![∫((x^3 +x^2 ))^(1/3) dx= [t=(x)^(1/3) → dx=3t^2 dt] =3∫t^4 ((t^3 +1))^(1/3) dt= [u=(((t^3 +1))^(1/3) /t) → du=−t^2 (((t^3 +1)^2 ))^(1/3) dt] =−3∫(u^3 /((u−1)^3 (u^2 +u+1)^3 ))du= [Ostrogradski′s Method: ∫((P(u))/(Q(u)))du=((P_1 (u))/(Q_1 (u)))+∫((P_2 (u))/(Q_2 (u)))du Q_1 (u)=gcd(Q(u), Q′(u))=u^6 −2u^3 +1 Q_2 (u)=((Q(u))/(Q_1 (u)))=u^3 −1 to find P_1 (u) and P_2 (u) we differentiate both sides: ((P(u))/(Q(u)))=(d/du)[((P_1 (u))/(Q_1 (u)))]+((P_2 (u))/(Q_2 (u))) with P_1 (u)=au^5 +bu^4 +cu^3 +du^2 +eu+f and P_2 (u)=gu^2 +hu+i solving for these constants we get P_1 (u)=−(1/(18))u^4 −(1/9)u P_2 (u)=−(1/9)] =((u(u^3 +2))/(6(u−1)^2 (u^2 +u+1)^2 ))+(1/3)∫(du/((u−1)(u^2 +u+1))) the first part is solved and equals (1/6)(3x+1)((x^3 +x^2 ))^(1/3) the second part: (1/3)∫(du/((u−1)(u^2 +u+1)))=(1/9)∫(du/(u−1))−(1/9)∫((u+2)/(u^2 +u+1))du the first is simply = (1/9)ln (u−1) = =(1/9)ln ((((x+1))^(1/3) −(x)^(1/3) )/( (x)^(1/3) )) the second part: −(1/9)∫((u+2)/(u^2 +u+1))du=−(1/(18))∫((2u+1)/(u^2 +u+1))du−(1/6)∫(du/(u^2 +u+1)) the first is simply = −(1/(18))ln (u^2 +u+1) = =−(1/(18))ln (1+(((x+1)/x))^(1/3) +(((((x+1)/x))^2 ))^(1/3) ) the second is simply = −((√3)/9)arctan (((2u+1)(√3))/3) = =−((√3)/9)arctan (((2((x+1))^(1/3) +(x)^(1/3) )(√3))/(3(x)^(1/3) )) so we get (1/6)(3x+1)((x^3 +x^2 ))^(1/3) +(1/9)ln ∣((((x+1))^(1/3) −(x)^(1/3) )/( (x)^(1/3) ))∣ −(1/(18))ln ∣1+(((x+1)/x))^(1/3) +(((((x+1)/x))^2 ))^(1/3) ∣ −((√3)/9)arctan (((2((x+1))^(1/3) +(x)^(1/3) )(√3))/(3(x)^(1/3) )) +C](https://www.tinkutara.com/question/Q55130.png)
$$\int\sqrt[{\mathrm{3}}]{{x}^{\mathrm{3}} +{x}^{\mathrm{2}} }{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\sqrt[{\mathrm{3}}]{{x}}\:\rightarrow\:{dx}=\mathrm{3}{t}^{\mathrm{2}} {dt}\right] \\ $$$$=\mathrm{3}\int{t}^{\mathrm{4}} \sqrt[{\mathrm{3}}]{{t}^{\mathrm{3}} +\mathrm{1}}{dt}= \\ $$$$\:\:\:\:\:\left[{u}=\frac{\sqrt[{\mathrm{3}}]{{t}^{\mathrm{3}} +\mathrm{1}}}{{t}}\:\rightarrow\:{du}=−{t}^{\mathrm{2}} \sqrt[{\mathrm{3}}]{\left({t}^{\mathrm{3}} +\mathrm{1}\right)^{\mathrm{2}} }{dt}\right] \\ $$$$=−\mathrm{3}\int\frac{{u}^{\mathrm{3}} }{\left({u}−\mathrm{1}\right)^{\mathrm{3}} \left({u}^{\mathrm{2}} +{u}+\mathrm{1}\right)^{\mathrm{3}} }{du}= \\ $$$$ \\ $$$$\:\:\:\:\:\left[\mathrm{Ostrogradski}'\mathrm{s}\:\mathrm{Method}:\right. \\ $$$$\:\:\:\:\:\:\int\frac{{P}\left({u}\right)}{{Q}\left({u}\right)}{du}=\frac{{P}_{\mathrm{1}} \left({u}\right)}{{Q}_{\mathrm{1}} \left({u}\right)}+\int\frac{{P}_{\mathrm{2}} \left({u}\right)}{{Q}_{\mathrm{2}} \left({u}\right)}{du} \\ $$$$\:\:\:\:\:\:{Q}_{\mathrm{1}} \left({u}\right)=\mathrm{gcd}\left({Q}\left({u}\right),\:{Q}'\left({u}\right)\right)={u}^{\mathrm{6}} −\mathrm{2}{u}^{\mathrm{3}} +\mathrm{1} \\ $$$$\:\:\:\:\:\:{Q}_{\mathrm{2}} \left({u}\right)=\frac{{Q}\left({u}\right)}{{Q}_{\mathrm{1}} \left({u}\right)}={u}^{\mathrm{3}} −\mathrm{1} \\ $$$$\:\:\:\:\:\:\mathrm{to}\:\mathrm{find}\:{P}_{\mathrm{1}} \left({u}\right)\:\mathrm{and}\:{P}_{\mathrm{2}} \left({u}\right)\:\mathrm{we}\:\mathrm{differentiate} \\ $$$$\:\:\:\:\:\:\mathrm{both}\:\mathrm{sides}: \\ $$$$\:\:\:\:\:\:\frac{{P}\left({u}\right)}{{Q}\left({u}\right)}=\frac{{d}}{{du}}\left[\frac{{P}_{\mathrm{1}} \left({u}\right)}{{Q}_{\mathrm{1}} \left({u}\right)}\right]+\frac{{P}_{\mathrm{2}} \left({u}\right)}{{Q}_{\mathrm{2}} \left({u}\right)} \\ $$$$\:\:\:\:\:\:\mathrm{with}\:{P}_{\mathrm{1}} \left({u}\right)={au}^{\mathrm{5}} +{bu}^{\mathrm{4}} +{cu}^{\mathrm{3}} +{du}^{\mathrm{2}} +{eu}+{f}\:\mathrm{and} \\ $$$$\:\:\:\:\:\:{P}_{\mathrm{2}} \left({u}\right)={gu}^{\mathrm{2}} +{hu}+{i} \\ $$$$\:\:\:\:\:\:\mathrm{solving}\:\mathrm{for}\:\mathrm{these}\:\mathrm{constants}\:\mathrm{we}\:\mathrm{get} \\ $$$$\:\:\:\:\:\:{P}_{\mathrm{1}} \left({u}\right)=−\frac{\mathrm{1}}{\mathrm{18}}{u}^{\mathrm{4}} −\frac{\mathrm{1}}{\mathrm{9}}{u} \\ $$$$\left.\:\:\:\:\:\:{P}_{\mathrm{2}} \left({u}\right)=−\frac{\mathrm{1}}{\mathrm{9}}\right] \\ $$$$ \\ $$$$=\frac{{u}\left({u}^{\mathrm{3}} +\mathrm{2}\right)}{\mathrm{6}\left({u}−\mathrm{1}\right)^{\mathrm{2}} \left({u}^{\mathrm{2}} +{u}+\mathrm{1}\right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{3}}\int\frac{{du}}{\left({u}−\mathrm{1}\right)\left({u}^{\mathrm{2}} +{u}+\mathrm{1}\right)} \\ $$$$\mathrm{the}\:\mathrm{first}\:\mathrm{part}\:\mathrm{is}\:\mathrm{solved}\:\mathrm{and}\:\mathrm{equals} \\ $$$$\frac{\mathrm{1}}{\mathrm{6}}\left(\mathrm{3}{x}+\mathrm{1}\right)\sqrt[{\mathrm{3}}]{{x}^{\mathrm{3}} +{x}^{\mathrm{2}} } \\ $$$$\mathrm{the}\:\mathrm{second}\:\mathrm{part}: \\ $$$$\frac{\mathrm{1}}{\mathrm{3}}\int\frac{{du}}{\left({u}−\mathrm{1}\right)\left({u}^{\mathrm{2}} +{u}+\mathrm{1}\right)}=\frac{\mathrm{1}}{\mathrm{9}}\int\frac{{du}}{{u}−\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{9}}\int\frac{{u}+\mathrm{2}}{{u}^{\mathrm{2}} +{u}+\mathrm{1}}{du} \\ $$$$\mathrm{the}\:\mathrm{first}\:\mathrm{is}\:\mathrm{simply}\:=\:\frac{\mathrm{1}}{\mathrm{9}}\mathrm{ln}\:\left({u}−\mathrm{1}\right)\:= \\ $$$$=\frac{\mathrm{1}}{\mathrm{9}}\mathrm{ln}\:\frac{\sqrt[{\mathrm{3}}]{{x}+\mathrm{1}}−\sqrt[{\mathrm{3}}]{{x}}}{\:\sqrt[{\mathrm{3}}]{{x}}} \\ $$$$\mathrm{the}\:\mathrm{second}\:\mathrm{part}: \\ $$$$−\frac{\mathrm{1}}{\mathrm{9}}\int\frac{{u}+\mathrm{2}}{{u}^{\mathrm{2}} +{u}+\mathrm{1}}{du}=−\frac{\mathrm{1}}{\mathrm{18}}\int\frac{\mathrm{2}{u}+\mathrm{1}}{{u}^{\mathrm{2}} +{u}+\mathrm{1}}{du}−\frac{\mathrm{1}}{\mathrm{6}}\int\frac{{du}}{{u}^{\mathrm{2}} +{u}+\mathrm{1}} \\ $$$$\mathrm{the}\:\mathrm{first}\:\mathrm{is}\:\mathrm{simply}\:=\:−\frac{\mathrm{1}}{\mathrm{18}}\mathrm{ln}\:\left({u}^{\mathrm{2}} +{u}+\mathrm{1}\right)\:= \\ $$$$=−\frac{\mathrm{1}}{\mathrm{18}}\mathrm{ln}\:\left(\mathrm{1}+\sqrt[{\mathrm{3}}]{\frac{{x}+\mathrm{1}}{{x}}}+\sqrt[{\mathrm{3}}]{\left(\frac{{x}+\mathrm{1}}{{x}}\right)^{\mathrm{2}} }\right) \\ $$$$\mathrm{the}\:\mathrm{second}\:\mathrm{is}\:\mathrm{simply}\:=\:−\frac{\sqrt{\mathrm{3}}}{\mathrm{9}}\mathrm{arctan}\:\frac{\left(\mathrm{2}{u}+\mathrm{1}\right)\sqrt{\mathrm{3}}}{\mathrm{3}}\:= \\ $$$$=−\frac{\sqrt{\mathrm{3}}}{\mathrm{9}}\mathrm{arctan}\:\frac{\left(\mathrm{2}\sqrt[{\mathrm{3}}]{{x}+\mathrm{1}}+\sqrt[{\mathrm{3}}]{{x}}\right)\sqrt{\mathrm{3}}}{\mathrm{3}\sqrt[{\mathrm{3}}]{{x}}} \\ $$$$ \\ $$$$\mathrm{so}\:\mathrm{we}\:\mathrm{get} \\ $$$$\frac{\mathrm{1}}{\mathrm{6}}\left(\mathrm{3}{x}+\mathrm{1}\right)\sqrt[{\mathrm{3}}]{{x}^{\mathrm{3}} +{x}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{9}}\mathrm{ln}\:\mid\frac{\sqrt[{\mathrm{3}}]{{x}+\mathrm{1}}−\sqrt[{\mathrm{3}}]{{x}}}{\:\sqrt[{\mathrm{3}}]{{x}}}\mid\:−\frac{\mathrm{1}}{\mathrm{18}}\mathrm{ln}\:\mid\mathrm{1}+\sqrt[{\mathrm{3}}]{\frac{{x}+\mathrm{1}}{{x}}}+\sqrt[{\mathrm{3}}]{\left(\frac{{x}+\mathrm{1}}{{x}}\right)^{\mathrm{2}} }\mid\:−\frac{\sqrt{\mathrm{3}}}{\mathrm{9}}\mathrm{arctan}\:\frac{\left(\mathrm{2}\sqrt[{\mathrm{3}}]{{x}+\mathrm{1}}+\sqrt[{\mathrm{3}}]{{x}}\right)\sqrt{\mathrm{3}}}{\mathrm{3}\sqrt[{\mathrm{3}}]{{x}}}\:+{C} \\ $$
Commented by MJS last updated on 18/Feb/19
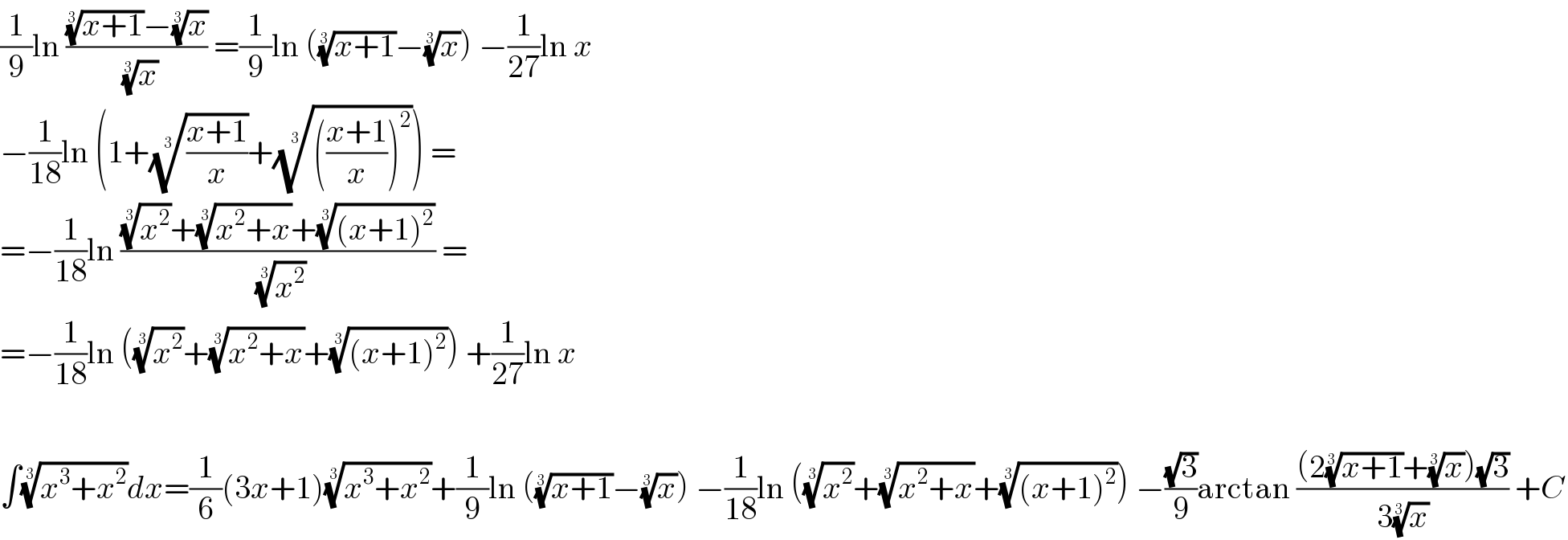
$$\frac{\mathrm{1}}{\mathrm{9}}\mathrm{ln}\:\frac{\sqrt[{\mathrm{3}}]{{x}+\mathrm{1}}−\sqrt[{\mathrm{3}}]{{x}}}{\:\sqrt[{\mathrm{3}}]{{x}}}\:=\frac{\mathrm{1}}{\mathrm{9}}\mathrm{ln}\:\left(\sqrt[{\mathrm{3}}]{{x}+\mathrm{1}}−\sqrt[{\mathrm{3}}]{{x}}\right)\:−\frac{\mathrm{1}}{\mathrm{27}}\mathrm{ln}\:{x} \\ $$$$−\frac{\mathrm{1}}{\mathrm{18}}\mathrm{ln}\:\left(\mathrm{1}+\sqrt[{\mathrm{3}}]{\frac{{x}+\mathrm{1}}{{x}}}+\sqrt[{\mathrm{3}}]{\left(\frac{{x}+\mathrm{1}}{{x}}\right)^{\mathrm{2}} }\right)\:= \\ $$$$=−\frac{\mathrm{1}}{\mathrm{18}}\mathrm{ln}\:\frac{\sqrt[{\mathrm{3}}]{{x}^{\mathrm{2}} }+\sqrt[{\mathrm{3}}]{{x}^{\mathrm{2}} +{x}}+\sqrt[{\mathrm{3}}]{\left({x}+\mathrm{1}\right)^{\mathrm{2}} }}{\:\sqrt[{\mathrm{3}}]{{x}^{\mathrm{2}} }}\:= \\ $$$$=−\frac{\mathrm{1}}{\mathrm{18}}\mathrm{ln}\:\left(\sqrt[{\mathrm{3}}]{{x}^{\mathrm{2}} }+\sqrt[{\mathrm{3}}]{{x}^{\mathrm{2}} +{x}}+\sqrt[{\mathrm{3}}]{\left({x}+\mathrm{1}\right)^{\mathrm{2}} }\right)\:+\frac{\mathrm{1}}{\mathrm{27}}\mathrm{ln}\:{x} \\ $$$$ \\ $$$$\int\sqrt[{\mathrm{3}}]{{x}^{\mathrm{3}} +{x}^{\mathrm{2}} }{dx}=\frac{\mathrm{1}}{\mathrm{6}}\left(\mathrm{3}{x}+\mathrm{1}\right)\sqrt[{\mathrm{3}}]{{x}^{\mathrm{3}} +{x}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{9}}\mathrm{ln}\:\left(\sqrt[{\mathrm{3}}]{{x}+\mathrm{1}}−\sqrt[{\mathrm{3}}]{{x}}\right)\:−\frac{\mathrm{1}}{\mathrm{18}}\mathrm{ln}\:\left(\sqrt[{\mathrm{3}}]{{x}^{\mathrm{2}} }+\sqrt[{\mathrm{3}}]{{x}^{\mathrm{2}} +{x}}+\sqrt[{\mathrm{3}}]{\left({x}+\mathrm{1}\right)^{\mathrm{2}} }\right)\:−\frac{\sqrt{\mathrm{3}}}{\mathrm{9}}\mathrm{arctan}\:\frac{\left(\mathrm{2}\sqrt[{\mathrm{3}}]{{x}+\mathrm{1}}+\sqrt[{\mathrm{3}}]{{x}}\right)\sqrt{\mathrm{3}}}{\mathrm{3}\sqrt[{\mathrm{3}}]{{x}}}\:+{C} \\ $$
Commented by peter frank last updated on 18/Feb/19

$$\mathrm{thank}\:\mathrm{you} \\ $$$$ \\ $$
