Question Number 55044 by behi83417@gmail.com last updated on 16/Feb/19
Commented by behi83417@gmail.com last updated on 16/Feb/19

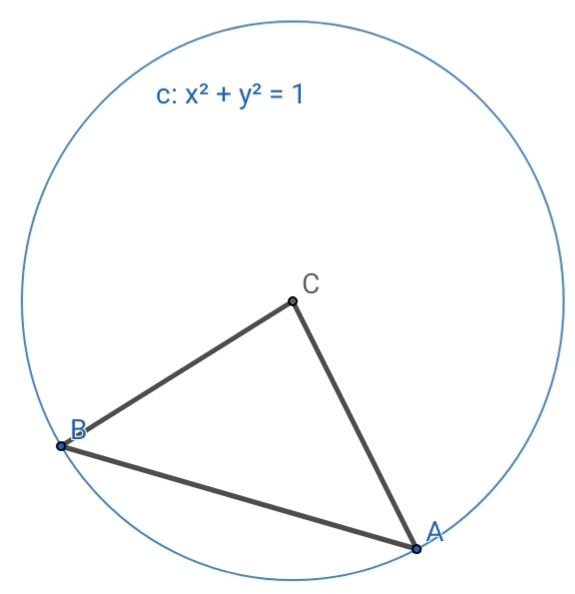
$${as}\:{shown}\:{in}\:{picture}: \\ $$$${find}\:{locus}\:{of}\:{centroid}\:{of}\:{triangle}: \\ $$$$\left.\mathrm{1}\right){when}:\boldsymbol{{B}}\:{and}\:\boldsymbol{{C}},{are}\:{fixed}\:{and}:\boldsymbol{{A}}\:{moves} \\ $$$${on}\:{the}\:{circle}'{s}\:\:{perimeter}. \\ $$$$\left.\mathrm{2}\right)\boldsymbol{{C}},{is}\:{fixed}\:{and}\:\boldsymbol{{A}}\:{and}\:\boldsymbol{{B}}\:\:{are}\:{moving}\:{on} \\ $$$${circle}'{s}\:{perimeter},\:{and}\:{perimeter}\:{of} \\ $$$${triangle}\:{is}\:{constant}\:{and}\:{equails}\:{to}:\mathrm{5}. \\ $$
Commented by mr W last updated on 17/Feb/19
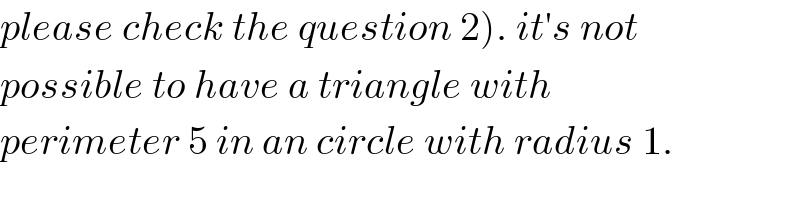
$$\left.{please}\:{check}\:{the}\:{question}\:\mathrm{2}\right).\:{it}'{s}\:{not} \\ $$$${possible}\:{to}\:{have}\:{a}\:{triangle}\:{with}\: \\ $$$${perimeter}\:\mathrm{5}\:{in}\:{an}\:{circle}\:{with}\:{radius}\:\mathrm{1}. \\ $$
Answered by mr W last updated on 17/Feb/19
Commented by mr W last updated on 17/Feb/19
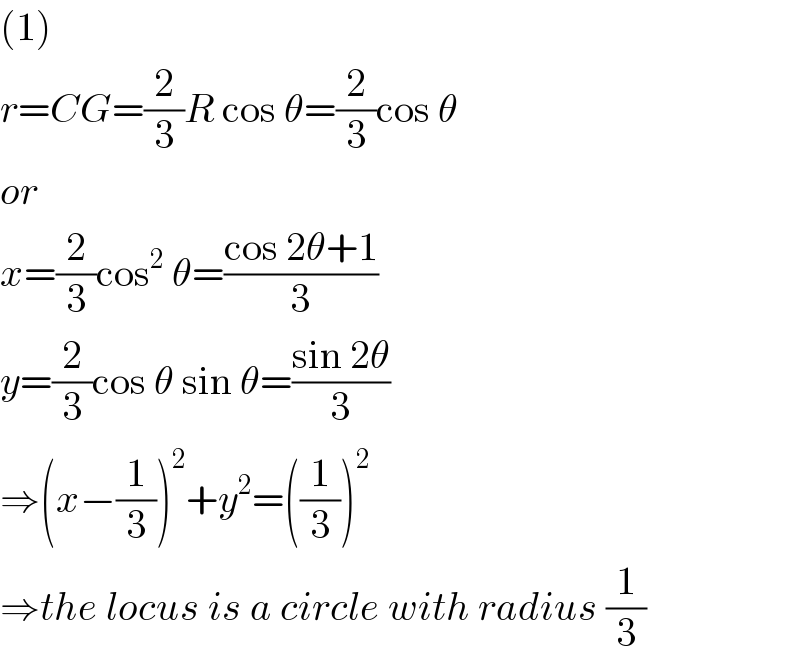
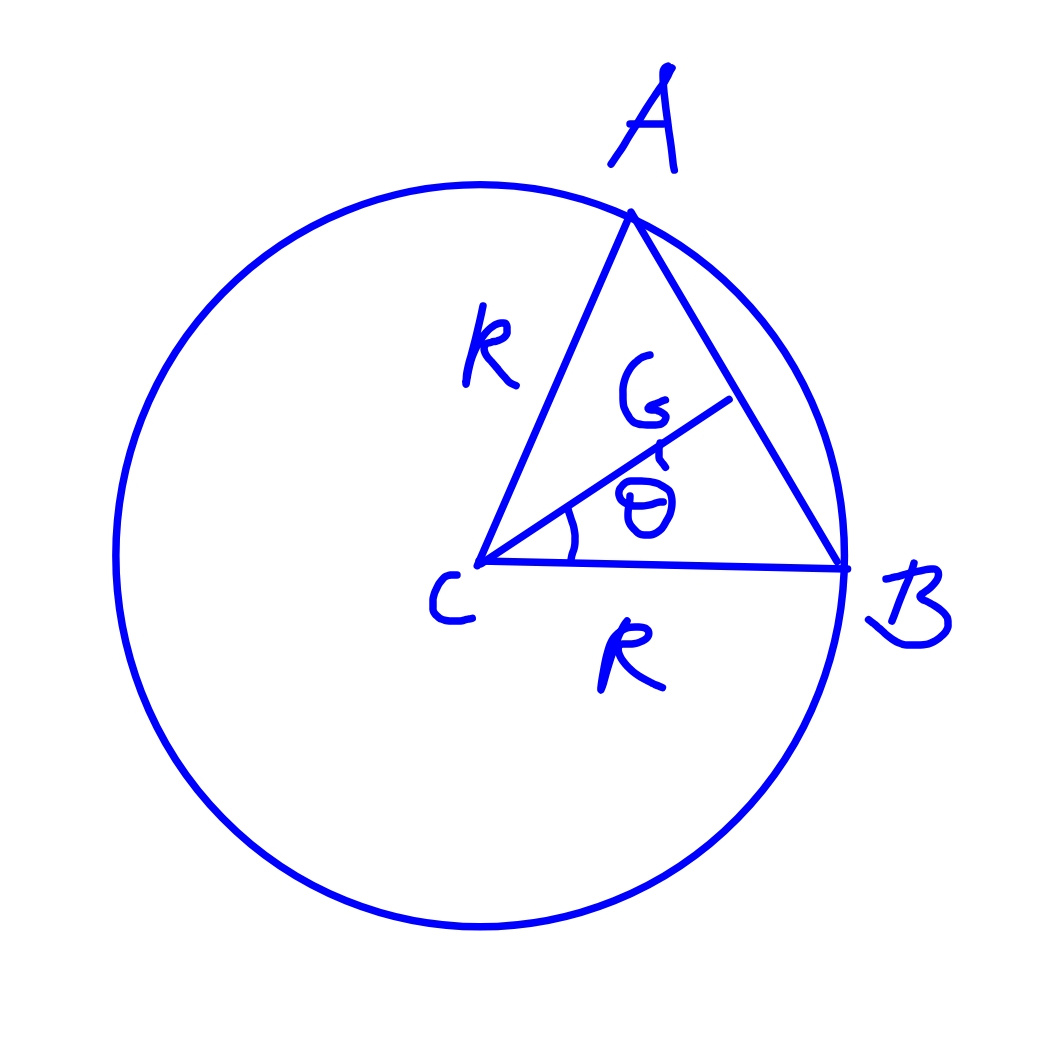
$$\left(\mathrm{1}\right) \\ $$$${r}={CG}=\frac{\mathrm{2}}{\mathrm{3}}{R}\:\mathrm{cos}\:\theta=\frac{\mathrm{2}}{\mathrm{3}}\mathrm{cos}\:\theta \\ $$$${or} \\ $$$${x}=\frac{\mathrm{2}}{\mathrm{3}}\mathrm{cos}^{\mathrm{2}} \:\theta=\frac{\mathrm{cos}\:\mathrm{2}\theta+\mathrm{1}}{\mathrm{3}} \\ $$$${y}=\frac{\mathrm{2}}{\mathrm{3}}\mathrm{cos}\:\theta\:\mathrm{sin}\:\theta=\frac{\mathrm{sin}\:\mathrm{2}\theta}{\mathrm{3}} \\ $$$$\Rightarrow\left({x}−\frac{\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} =\left(\frac{\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{2}} \\ $$$$\Rightarrow{the}\:{locus}\:{is}\:{a}\:{circle}\:{with}\:{radius}\:\frac{\mathrm{1}}{\mathrm{3}} \\ $$
Commented by mr W last updated on 17/Feb/19
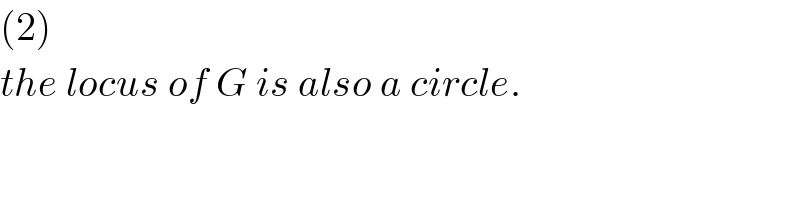
$$\left(\mathrm{2}\right) \\ $$$${the}\:{locus}\:{of}\:{G}\:{is}\:{also}\:{a}\:{circle}. \\ $$
