Question Number 55055 by peter frank last updated on 16/Feb/19

Answered by mr W last updated on 16/Feb/19
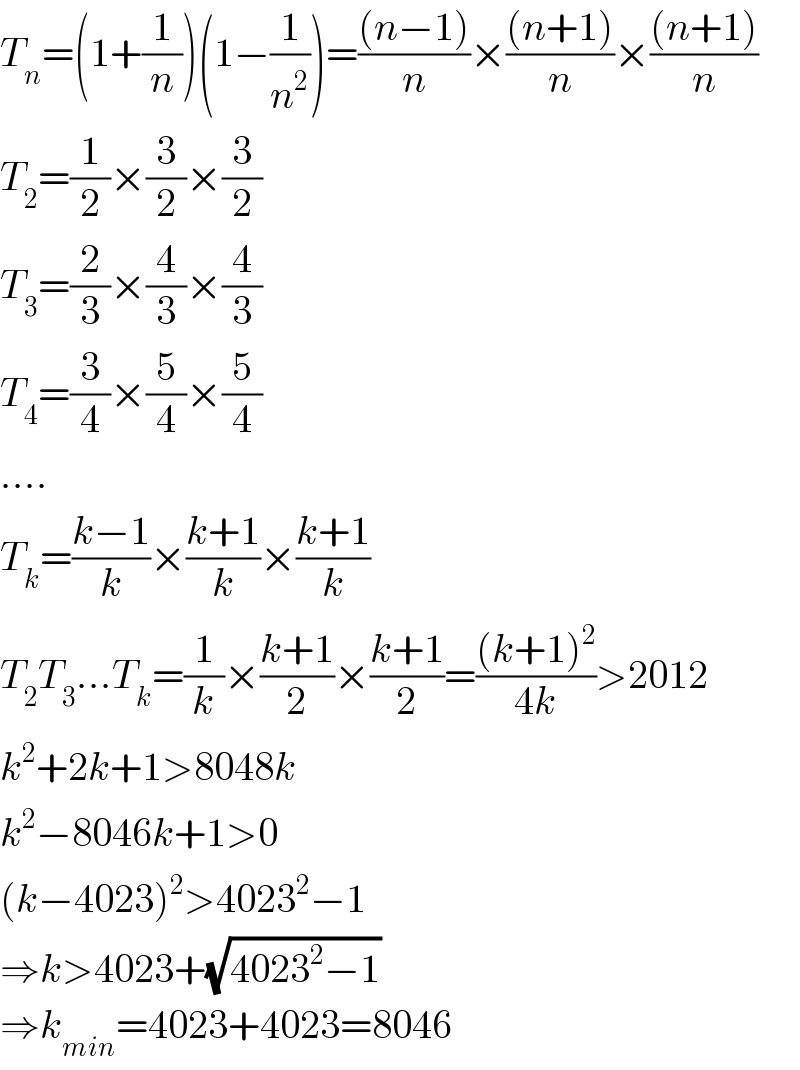
$${T}_{{n}} =\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right)\left(\mathrm{1}−\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\right)=\frac{\left({n}−\mathrm{1}\right)}{{n}}×\frac{\left({n}+\mathrm{1}\right)}{{n}}×\frac{\left({n}+\mathrm{1}\right)}{{n}} \\ $$$${T}_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{3}}{\mathrm{2}}×\frac{\mathrm{3}}{\mathrm{2}} \\ $$$${T}_{\mathrm{3}} =\frac{\mathrm{2}}{\mathrm{3}}×\frac{\mathrm{4}}{\mathrm{3}}×\frac{\mathrm{4}}{\mathrm{3}} \\ $$$${T}_{\mathrm{4}} =\frac{\mathrm{3}}{\mathrm{4}}×\frac{\mathrm{5}}{\mathrm{4}}×\frac{\mathrm{5}}{\mathrm{4}} \\ $$$$…. \\ $$$${T}_{{k}} =\frac{{k}−\mathrm{1}}{{k}}×\frac{{k}+\mathrm{1}}{{k}}×\frac{{k}+\mathrm{1}}{{k}} \\ $$$${T}_{\mathrm{2}} {T}_{\mathrm{3}} …{T}_{{k}} =\frac{\mathrm{1}}{{k}}×\frac{{k}+\mathrm{1}}{\mathrm{2}}×\frac{{k}+\mathrm{1}}{\mathrm{2}}=\frac{\left({k}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{4}{k}}>\mathrm{2012} \\ $$$${k}^{\mathrm{2}} +\mathrm{2}{k}+\mathrm{1}>\mathrm{8048}{k} \\ $$$${k}^{\mathrm{2}} −\mathrm{8046}{k}+\mathrm{1}>\mathrm{0} \\ $$$$\left({k}−\mathrm{4023}\right)^{\mathrm{2}} >\mathrm{4023}^{\mathrm{2}} −\mathrm{1} \\ $$$$\Rightarrow{k}>\mathrm{4023}+\sqrt{\mathrm{4023}^{\mathrm{2}} −\mathrm{1}} \\ $$$$\Rightarrow{k}_{{min}} =\mathrm{4023}+\mathrm{4023}=\mathrm{8046} \\ $$
