Question Number 55149 by pooja24 last updated on 18/Feb/19
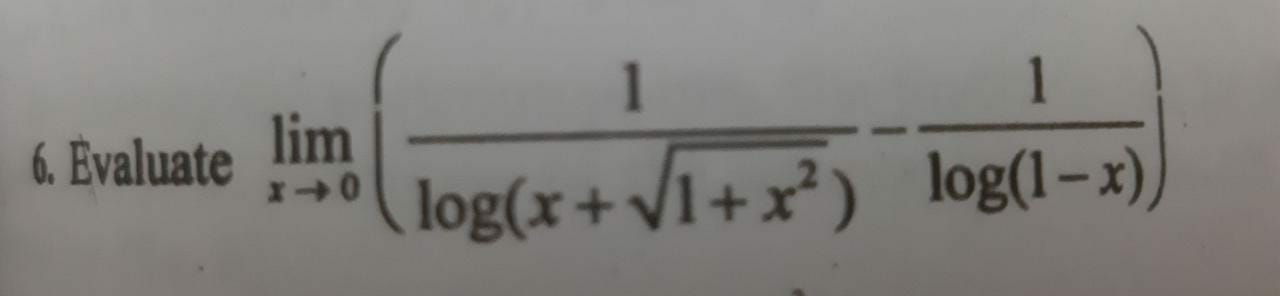
Answered by tanmay.chaudhury50@gmail.com last updated on 18/Feb/19
![li_(x→0) x=tanθ as x→0 θ→0 lim_(θ→0) (1/(ln(tanθ+secθ)))−(1/(ln(1−tanθ))) lim_(θ→0) (1/({ln(((1+sinθ)/(cosθ)))}))−(1/(ln(1−tanθ))) t=tan(θ/2) as θ→0 t→0 lim_(t→0) (1/({ln(((1+((2t)/(1+t^2 )))/(((1+t)(1−t))/(1+t^2 ))))}))−(1/(ln(1−((2t)/(1−t^2 ))))) lim_(t→0) (1/(ln(((1+t)/(1−t)))))−(1/(ln(1−((2t)/(1−t^2 ))))) lim_(t→0) (1/p)−(1/q) now..lim_(t→0) (1/p) value is lim_(t→0) (1/(((ln(1+t))/t)×t−((ln(1−t))/(−t))×−t)) lim_(t→0) (1/(t+t))→lim_(t→0) (1/(2t))....[wait] now lim_(t→0) (1/q) lim_(t→0) (1/(ln(1−((2t)/(1−t^2 ))))) lim_(t→0) (1/([((ln(1−((2t)/(1−t^2 ))))/((−2t)/(1−t^2 )))]×((−2t)/(1−t^2 )))) lim_(t→0) ((1−t^2 )/(−2t)) now combining... lim_(t→0) [(1/(2t))−(((1−t^2 )/(−2t)))] lim_(t→0) ((1+1−t^2 )/(2t)) using L H rule lim_(t→0) ((0−2t)/2) so answer is 0 pls other check...](https://www.tinkutara.com/question/Q55155.png)
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{li}} \\ $$$${x}={tan}\theta\:\:\:\:{as}\:{x}\rightarrow\mathrm{0}\:\:\theta\rightarrow\mathrm{0} \\ $$$$\underset{\theta\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:\frac{\mathrm{1}}{{ln}\left({tan}\theta+{sec}\theta\right)}−\frac{\mathrm{1}}{{ln}\left(\mathrm{1}−{tan}\theta\right)} \\ $$$$\underset{\theta\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}}{\left\{{ln}\left(\frac{\mathrm{1}+{sin}\theta}{{cos}\theta}\right)\right\}}−\frac{\mathrm{1}}{{ln}\left(\mathrm{1}−{tan}\theta\right)} \\ $$$${t}={tan}\frac{\theta}{\mathrm{2}}\:\:\:{as}\:\theta\rightarrow\mathrm{0}\:\:\:{t}\rightarrow\mathrm{0} \\ $$$$\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:\frac{\mathrm{1}}{\left\{{ln}\left(\frac{\mathrm{1}+\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }}{\frac{\left(\mathrm{1}+{t}\right)\left(\mathrm{1}−{t}\right)}{\mathrm{1}+{t}^{\mathrm{2}} }}\right)\right\}}−\frac{\mathrm{1}}{{ln}\left(\mathrm{1}−\frac{\mathrm{2}{t}}{\mathrm{1}−{t}^{\mathrm{2}} }\right)} \\ $$$$\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}}{{ln}\left(\frac{\mathrm{1}+{t}}{\mathrm{1}−{t}}\right)}−\frac{\mathrm{1}}{{ln}\left(\mathrm{1}−\frac{\mathrm{2}{t}}{\mathrm{1}−{t}^{\mathrm{2}} }\right)} \\ $$$$\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}}{{p}}−\frac{\mathrm{1}}{{q}} \\ $$$${now}..\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}}{{p}}\:{value}\:{is} \\ $$$$\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}}{\frac{{ln}\left(\mathrm{1}+{t}\right)}{{t}}×{t}−\frac{{ln}\left(\mathrm{1}−{t}\right)}{−{t}}×−{t}} \\ $$$$\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}}{{t}+{t}}\rightarrow\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}}{\mathrm{2}{t}}….\left[{wait}\right] \\ $$$${now}\:\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}}{{q}} \\ $$$$\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}}{{ln}\left(\mathrm{1}−\frac{\mathrm{2}{t}}{\mathrm{1}−{t}^{\mathrm{2}} }\right)} \\ $$$$\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}}{\left[\frac{{ln}\left(\mathrm{1}−\frac{\mathrm{2}{t}}{\mathrm{1}−{t}^{\mathrm{2}} }\right)}{\frac{−\mathrm{2}{t}}{\mathrm{1}−{t}^{\mathrm{2}} }}\right]×\frac{−\mathrm{2}{t}}{\mathrm{1}−{t}^{\mathrm{2}} }} \\ $$$$\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}−{t}^{\mathrm{2}} }{−\mathrm{2}{t}} \\ $$$${now}\:{combining}… \\ $$$$\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left[\frac{\mathrm{1}}{\mathrm{2}{t}}−\left(\frac{\mathrm{1}−{t}^{\mathrm{2}} }{−\mathrm{2}{t}}\right)\right] \\ $$$$\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}+\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{2}{t}} \\ $$$${using}\:{L}\:{H}\:{rule} \\ $$$$\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{0}−\mathrm{2}{t}}{\mathrm{2}} \\ $$$${so}\:{answer}\:{is}\:\mathrm{0} \\ $$$${pls}\:{other}\:{check}… \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
