Question Number 55166 by Gulay last updated on 18/Feb/19
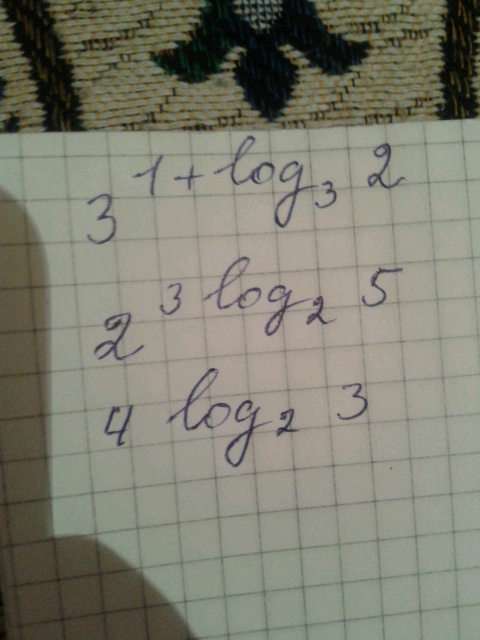
Answered by kaivan.ahmadi last updated on 18/Feb/19
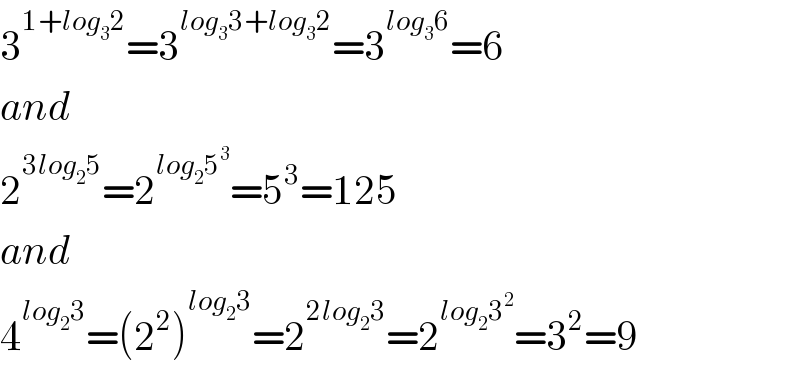
$$\mathrm{3}^{\mathrm{1}+{log}_{\mathrm{3}} \mathrm{2}} =\mathrm{3}^{{log}_{\mathrm{3}} \mathrm{3}+{log}_{\mathrm{3}} \mathrm{2}} =\mathrm{3}^{{log}_{\mathrm{3}} \mathrm{6}} =\mathrm{6} \\ $$$${and} \\ $$$$\mathrm{2}^{\mathrm{3}{log}_{\mathrm{2}} \mathrm{5}} =\mathrm{2}^{{log}_{\mathrm{2}} \mathrm{5}^{\mathrm{3}} } =\mathrm{5}^{\mathrm{3}} =\mathrm{125} \\ $$$${and} \\ $$$$\mathrm{4}^{{log}_{\mathrm{2}} \mathrm{3}} =\left(\mathrm{2}^{\mathrm{2}} \right)^{{log}_{\mathrm{2}} \mathrm{3}} =\mathrm{2}^{\mathrm{2}{log}_{\mathrm{2}} \mathrm{3}} =\mathrm{2}^{{log}_{\mathrm{2}} \mathrm{3}^{\mathrm{2}} } =\mathrm{3}^{\mathrm{2}} =\mathrm{9} \\ $$
Commented by Gulay last updated on 19/Feb/19

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$$$ \\ $$
