Question Number 55217 by peter frank last updated on 19/Feb/19

Answered by mr W last updated on 19/Feb/19
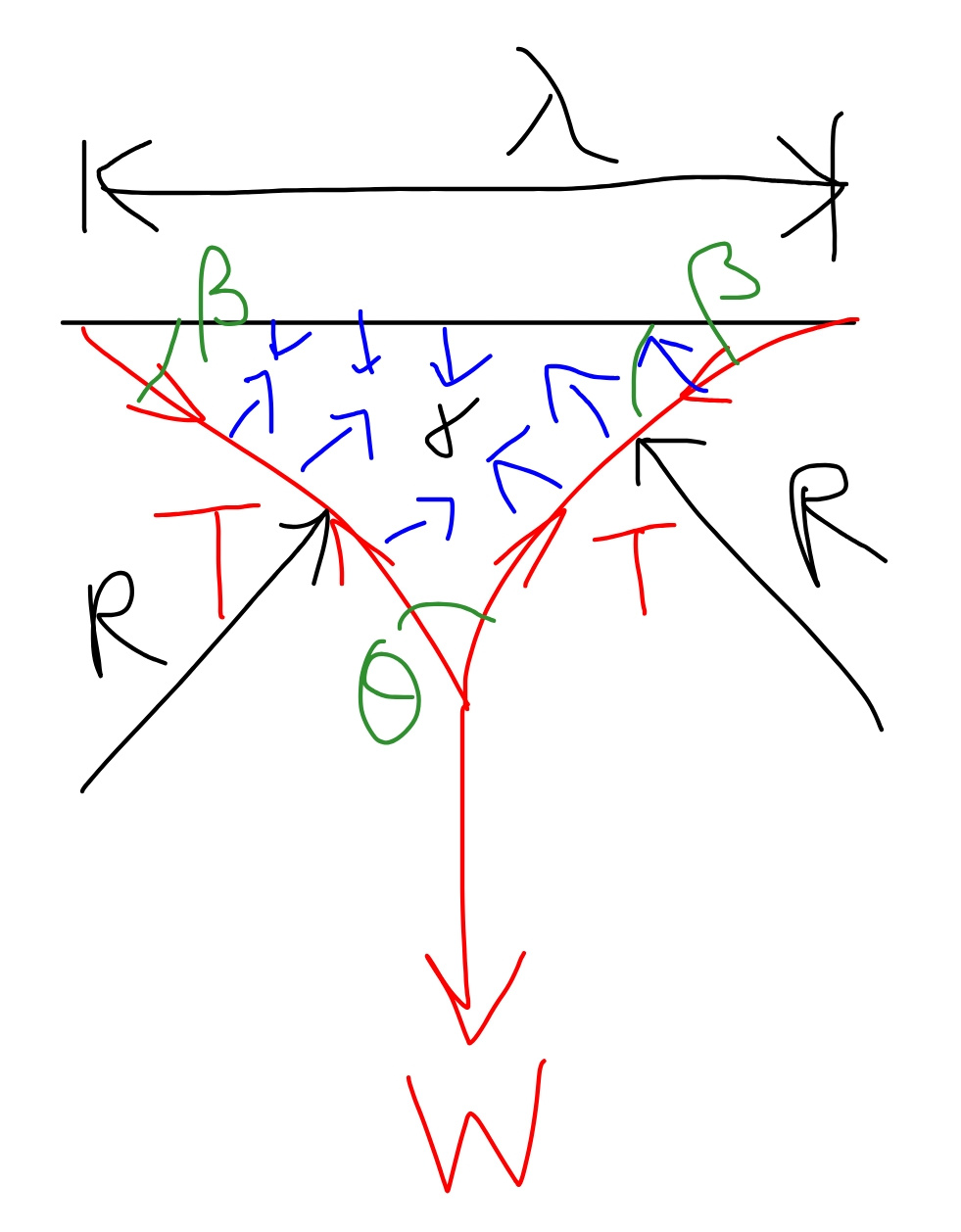
Commented by mr W last updated on 20/Feb/19
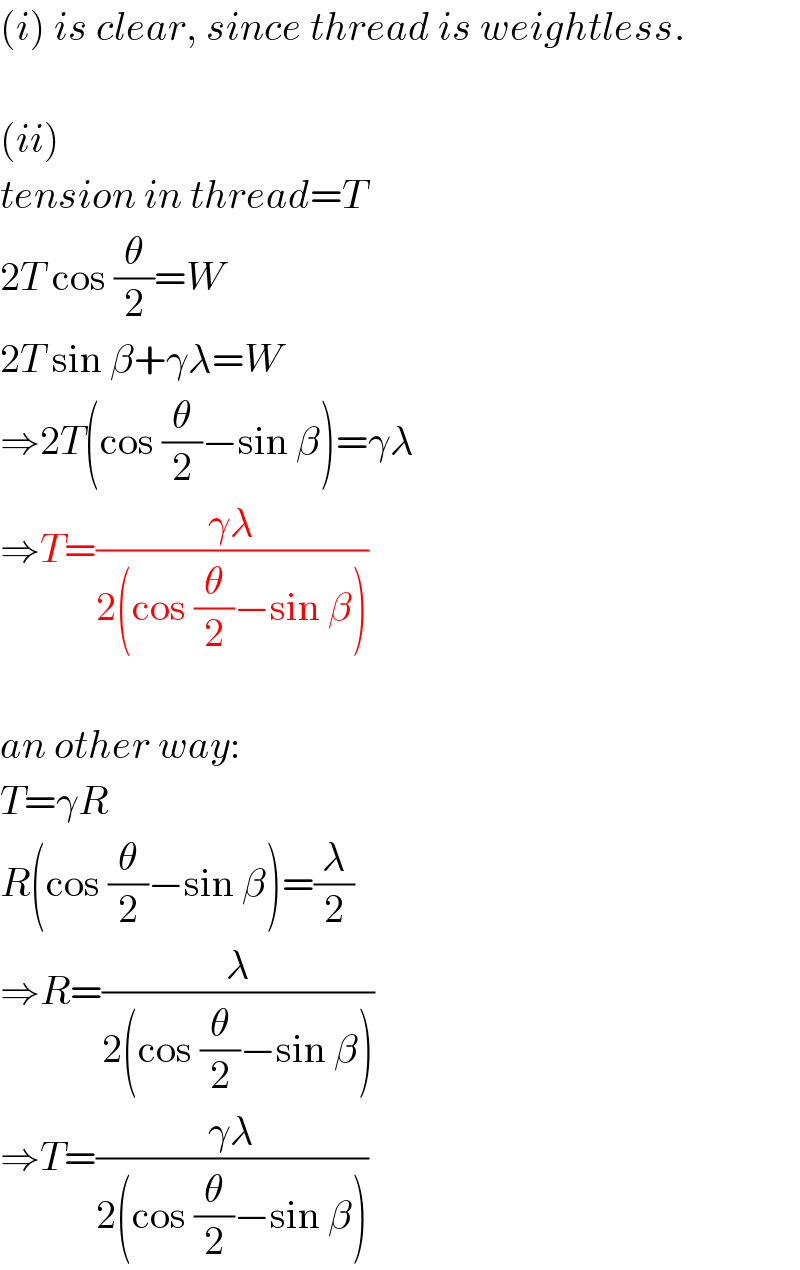
$$\left({i}\right)\:{is}\:{clear},\:{since}\:{thread}\:{is}\:{weightless}. \\ $$$$ \\ $$$$\left({ii}\right) \\ $$$${tension}\:{in}\:{thread}={T} \\ $$$$\mathrm{2}{T}\:\mathrm{cos}\:\frac{\theta}{\mathrm{2}}={W} \\ $$$$\mathrm{2}{T}\:\mathrm{sin}\:\beta+\gamma\lambda={W} \\ $$$$\Rightarrow\mathrm{2}{T}\left(\mathrm{cos}\:\frac{\theta}{\mathrm{2}}−\mathrm{sin}\:\beta\right)=\gamma\lambda \\ $$$$\Rightarrow{T}=\frac{\gamma\lambda}{\mathrm{2}\left(\mathrm{cos}\:\frac{\theta}{\mathrm{2}}−\mathrm{sin}\:\beta\right)} \\ $$$$ \\ $$$${an}\:{other}\:{way}: \\ $$$${T}=\gamma{R} \\ $$$${R}\left(\mathrm{cos}\:\frac{\theta}{\mathrm{2}}−\mathrm{sin}\:\beta\right)=\frac{\lambda}{\mathrm{2}} \\ $$$$\Rightarrow{R}=\frac{\lambda}{\mathrm{2}\left(\mathrm{cos}\:\frac{\theta}{\mathrm{2}}−\mathrm{sin}\:\beta\right)} \\ $$$$\Rightarrow{T}=\frac{\gamma\lambda}{\mathrm{2}\left(\mathrm{cos}\:\frac{\theta}{\mathrm{2}}−\mathrm{sin}\:\beta\right)} \\ $$
Commented by peter frank last updated on 20/Feb/19

$$\mathrm{why}\:\mathrm{cos}\:\frac{\theta}{\mathrm{2}}? \\ $$
Commented by mr W last updated on 20/Feb/19

$${you}\:{can}\:{see}\:{in}\:{my}\:{diagram}.\:{if}\:\theta\:{is} \\ $$$${the}\:{angle}\:{between}\:{the}\:{two}\:{parts}\:{of} \\ $$$${the}\:{thread}\:{at}\:{midpoint},\:{then}\:\frac{\theta}{\mathrm{2}}\:{is} \\ $$$${the}\:{angle}\:{between}\:{thread}\:{and}\:{vertical} \\ $$$${direction}. \\ $$
Commented by mr W last updated on 20/Feb/19
$${or}\:{you}\:{draw}\:{a}\:{diagram}\:{showing}\:{which} \\ $$$${angles}\:{are}\:{meant}\:{with}\:\beta\:{and}\:\theta\:{in}\:{the} \\ $$$${question}. \\ $$
Commented by peter frank last updated on 22/Feb/19

$$\mathrm{thank}\:\mathrm{sir} \\ $$
