Menu Close

Question-55223

Tinku Tara 0 Comments
Pin




Question Number 55223 by peter frank last updated on 19/Feb/19
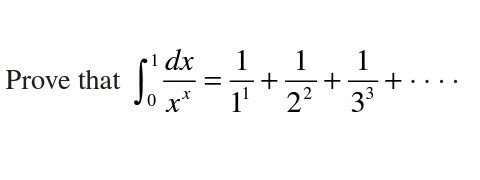
Commented by maxmathsup by imad last updated on 19/Feb/19
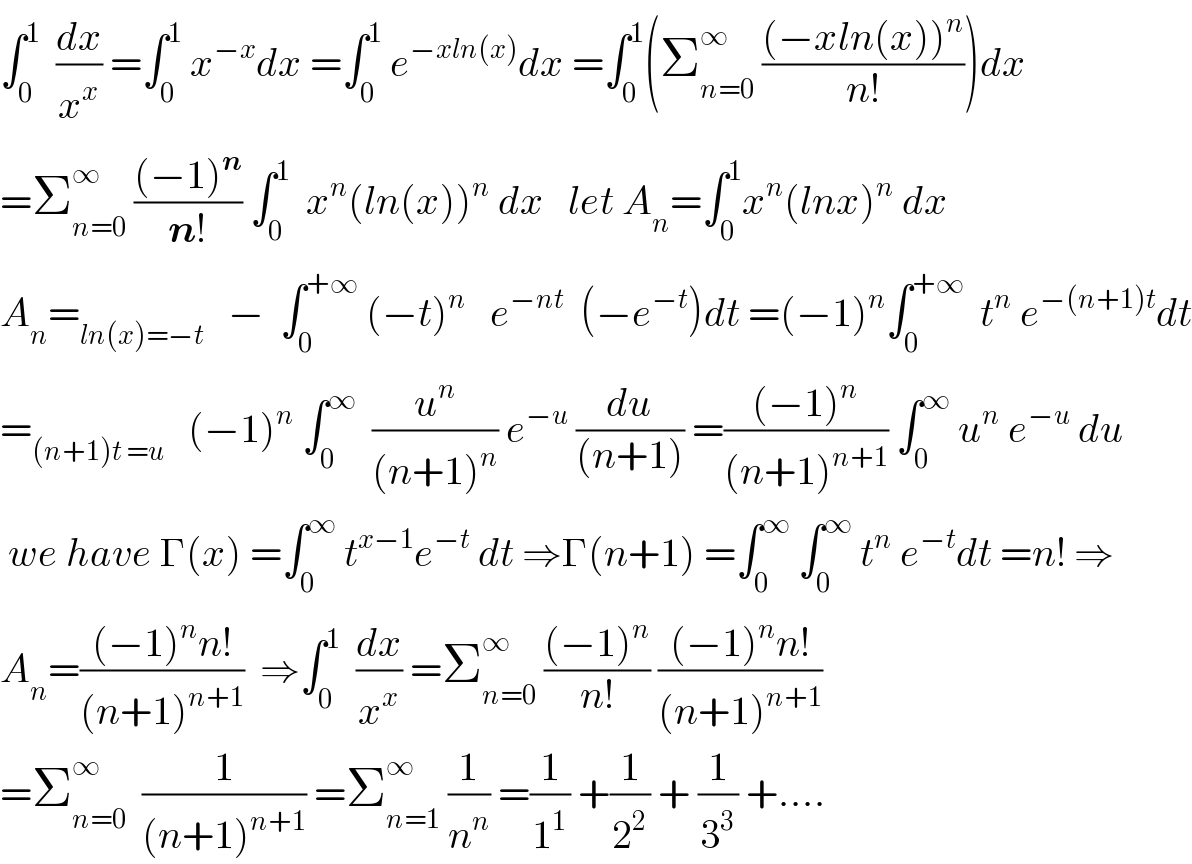
∫_0 ^1 (dx/x^x ) =∫_0 ^1 x^(−x) dx =∫_0 ^1 e^(−xln(x)) dx =∫_0 ^1 (Σ_(n=0) ^∞ (((−xln(x))^n )/(n!)))dx =Σ_(n=0) ^∞ (((−1)^n )/(n!)) ∫_0 ^1 x^n (ln(x))^n dx let A_n =∫_0 ^1 x^n (lnx)^n dx A_n =_(ln(x)=−t) − ∫_0 ^(+∞) (−t)^n e^(−nt) (−e^(−t) )dt =(−1)^n ∫_0 ^(+∞) t^n e^(−(n+1)t) dt =_((n+1)t =u) (−1)^n ∫_0 ^∞ (u^n /((n+1)^n )) e^(−u) (du/((n+1))) =(((−1)^n )/((n+1)^(n+1) )) ∫_0 ^∞ u^n e^(−u) du we have Γ(x) =∫_0 ^∞ t^(x−1) e^(−t) dt ⇒Γ(n+1) =∫_0 ^∞ ∫_0 ^∞ t^n e^(−t) dt =n! ⇒ A_n =(((−1)^n n!)/((n+1)^(n+1) )) ⇒∫_0 ^1 (dx/x^x ) =Σ_(n=0) ^∞ (((−1)^n )/(n!)) (((−1)^n n!)/((n+1)^(n+1) )) =Σ_(n=0) ^∞ (1/((n+1)^(n+1) )) =Σ_(n=1) ^∞ (1/n^n ) =(1/1^1 ) +(1/2^2 ) + (1/3^3 ) +....
$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{dx}}{{x}^{{x}} }\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:{x}^{−{x}} {dx}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:{e}^{−{xln}\left({x}\right)} {dx}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \left(\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−{xln}\left({x}\right)\right)^{{n}} }{{n}!}\right){dx} \\ $$$$=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\boldsymbol{{n}}} }{\boldsymbol{{n}}!}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:{x}^{{n}} \left({ln}\left({x}\right)\right)^{{n}} \:{dx}\:\:\:{let}\:{A}_{{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{n}} \left({lnx}\right)^{{n}} \:{dx} \\ $$$${A}_{{n}} =_{{ln}\left({x}\right)=−{t}} \:\:\:−\:\:\int_{\mathrm{0}} ^{+\infty} \:\left(−{t}\right)^{{n}} \:\:\:{e}^{−{nt}} \:\:\left(−{e}^{−{t}} \right){dt}\:=\left(−\mathrm{1}\right)^{{n}} \int_{\mathrm{0}} ^{+\infty} \:\:{t}^{{n}} \:{e}^{−\left({n}+\mathrm{1}\right){t}} {dt} \\ $$$$=_{\left({n}+\mathrm{1}\right){t}\:={u}} \:\:\:\left(−\mathrm{1}\right)^{{n}} \:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{u}^{{n}} }{\left({n}+\mathrm{1}\right)^{{n}} }\:{e}^{−{u}} \:\frac{{du}}{\left({n}+\mathrm{1}\right)}\:=\frac{\left(−\mathrm{1}\right)^{{n}} }{\left({n}+\mathrm{1}\right)^{{n}+\mathrm{1}} }\:\int_{\mathrm{0}} ^{\infty} \:{u}^{{n}} \:{e}^{−{u}} \:{du} \\ $$$$\:{we}\:{have}\:\Gamma\left({x}\right)\:=\int_{\mathrm{0}} ^{\infty} \:{t}^{{x}−\mathrm{1}} {e}^{−{t}} \:{dt}\:\Rightarrow\Gamma\left({n}+\mathrm{1}\right)\:=\int_{\mathrm{0}} ^{\infty} \:\int_{\mathrm{0}} ^{\infty} \:{t}^{{n}} \:{e}^{−{t}} {dt}\:={n}!\:\Rightarrow \\ $$$${A}_{{n}} =\frac{\left(−\mathrm{1}\right)^{{n}} {n}!}{\left({n}+\mathrm{1}\right)^{{n}+\mathrm{1}} }\:\:\Rightarrow\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{dx}}{{x}^{{x}} }\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}!}\:\frac{\left(−\mathrm{1}\right)^{{n}} {n}!}{\left({n}+\mathrm{1}\right)^{{n}+\mathrm{1}} } \\ $$$$=\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)^{{n}+\mathrm{1}} }\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{{n}^{{n}} }\:=\frac{\mathrm{1}}{\mathrm{1}^{\mathrm{1}} }\:+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }\:+\:\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{3}} }\:+…. \\ $$
Commented by maxmathsup by imad last updated on 19/Feb/19
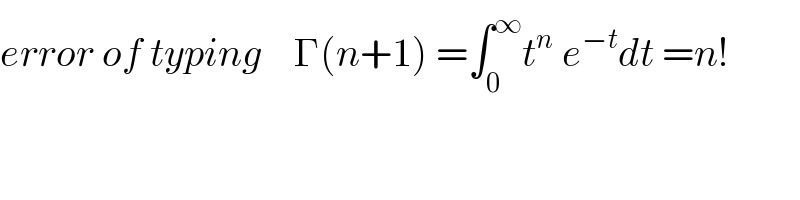
error of typing Γ(n+1) =∫_0 ^∞ t^n e^(−t) dt =n!
$${error}\:{of}\:{typing}\:\:\:\:\Gamma\left({n}+\mathrm{1}\right)\:=\int_{\mathrm{0}} ^{\infty} {t}^{{n}} \:{e}^{−{t}} {dt}\:={n}! \\ $$
Commented by peter frank last updated on 19/Feb/19
thank you
$$\mathrm{thank}\:\mathrm{you} \\ $$
Commented by peter frank last updated on 20/Feb/19
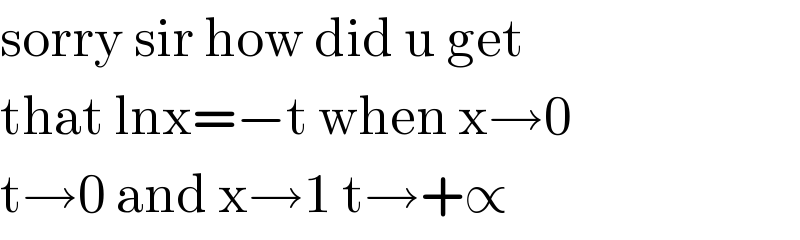
sorry sir how did u get that lnx=−t when x→0 t→0 and x→1 t→+∝
$$\mathrm{sorry}\:\mathrm{sir}\:\mathrm{how}\:\mathrm{did}\:\mathrm{u}\:\mathrm{get}\: \\ $$$$\mathrm{that}\:\mathrm{lnx}=−\mathrm{t}\:\mathrm{when}\:\mathrm{x}\rightarrow\mathrm{0} \\ $$$$\mathrm{t}\rightarrow\mathrm{0}\:\mathrm{and}\:\mathrm{x}\rightarrow\mathrm{1}\:\mathrm{t}\rightarrow+\propto \\ $$
Commented by maxmathsup by imad last updated on 24/Feb/19
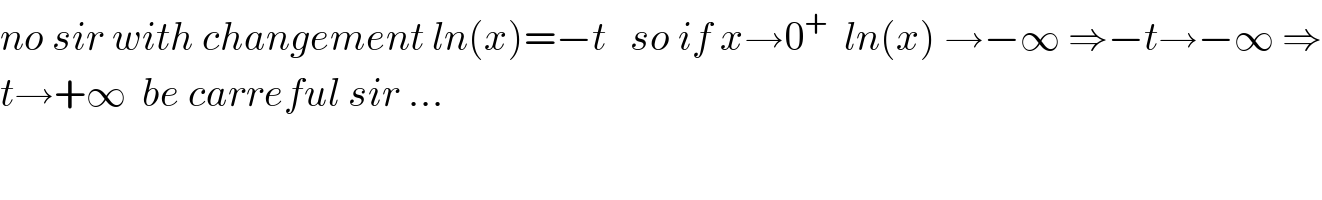
no sir with changement ln(x)=−t so if x→0^+ ln(x) →−∞ ⇒−t→−∞ ⇒ t→+∞ be carreful sir ...
$${no}\:{sir}\:{with}\:{changement}\:{ln}\left({x}\right)=−{t}\:\:\:{so}\:{if}\:{x}\rightarrow\mathrm{0}^{+} \:\:{ln}\left({x}\right)\:\rightarrow−\infty\:\Rightarrow−{t}\rightarrow−\infty\:\Rightarrow \\ $$$${t}\rightarrow+\infty\:\:{be}\:{carreful}\:{sir}\:… \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *