Question Number 55245 by Tawa1 last updated on 20/Feb/19

Answered by tanmay.chaudhury50@gmail.com last updated on 20/Feb/19
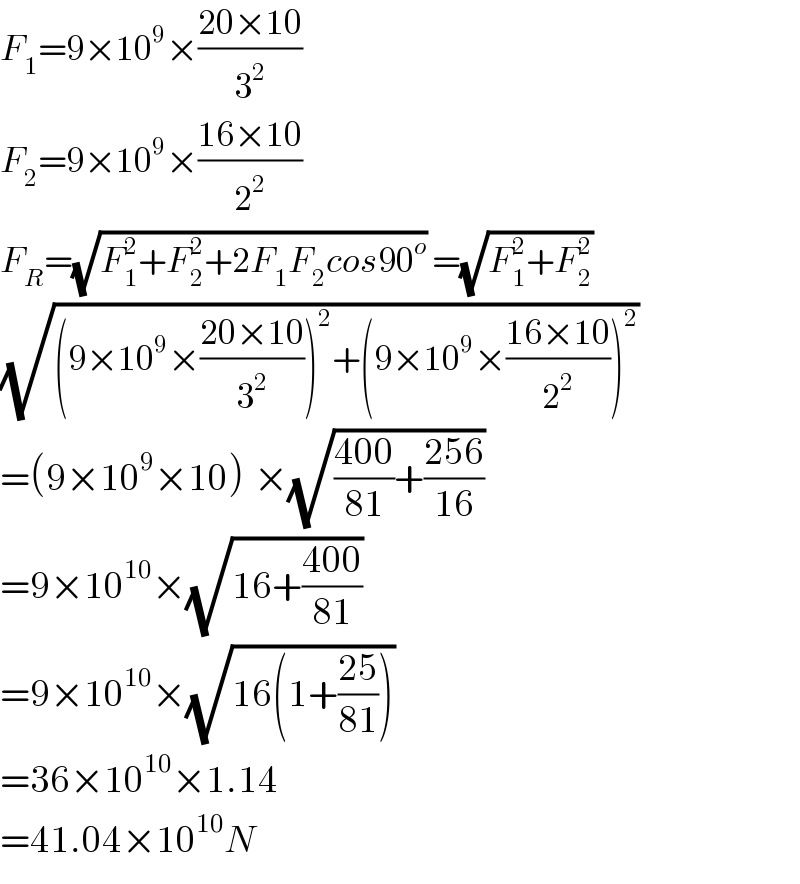
$${F}_{\mathrm{1}} =\mathrm{9}×\mathrm{10}^{\mathrm{9}} ×\frac{\mathrm{20}×\mathrm{10}}{\mathrm{3}^{\mathrm{2}} } \\ $$$${F}_{\mathrm{2}} =\mathrm{9}×\mathrm{10}^{\mathrm{9}} ×\frac{\mathrm{16}×\mathrm{10}}{\mathrm{2}^{\mathrm{2}} } \\ $$$${F}_{{R}} =\sqrt{{F}_{\mathrm{1}} ^{\mathrm{2}} +{F}_{\mathrm{2}} ^{\mathrm{2}} +\mathrm{2}{F}_{\mathrm{1}} {F}_{\mathrm{2}} {cos}\mathrm{90}^{{o}} }\:=\sqrt{{F}_{\mathrm{1}} ^{\mathrm{2}} +{F}_{\mathrm{2}} ^{\mathrm{2}} }\: \\ $$$$\sqrt{\left(\mathrm{9}×\mathrm{10}^{\mathrm{9}} ×\frac{\mathrm{20}×\mathrm{10}}{\mathrm{3}^{\mathrm{2}} }\right)^{\mathrm{2}} +\left(\mathrm{9}×\mathrm{10}^{\mathrm{9}} ×\frac{\mathrm{16}×\mathrm{10}}{\mathrm{2}^{\mathrm{2}} }\right)^{\mathrm{2}} }\: \\ $$$$=\left(\mathrm{9}×\mathrm{10}^{\mathrm{9}} ×\mathrm{10}\right)^{} ×\sqrt{\frac{\mathrm{400}}{\mathrm{81}}+\frac{\mathrm{256}}{\mathrm{16}}}\: \\ $$$$=\mathrm{9}×\mathrm{10}^{\mathrm{10}} ×\sqrt{\mathrm{16}+\frac{\mathrm{400}}{\mathrm{81}}}\: \\ $$$$=\mathrm{9}×\mathrm{10}^{\mathrm{10}} ×\sqrt{\mathrm{16}\left(\mathrm{1}+\frac{\mathrm{25}}{\mathrm{81}}\right)}\: \\ $$$$=\mathrm{36}×\mathrm{10}^{\mathrm{10}} ×\mathrm{1}.\mathrm{14} \\ $$$$=\mathrm{41}.\mathrm{04}×\mathrm{10}^{\mathrm{10}} {N} \\ $$
Commented by Tawa1 last updated on 20/Feb/19

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$$$\mathrm{But}\:\mathrm{sir},\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\:\mathrm{F}_{\mathrm{R}} \:\mathrm{very}\:\mathrm{wide}.\:\:\mathrm{Hope}\:\mathrm{the}\:\mathrm{answer}\:\mathrm{will}\:\mathrm{be}\:\mathrm{right}. \\ $$$$\mathrm{i}\:\mathrm{used}\:\mathrm{your}\:\mathrm{formular}\:\mathrm{and}\:\mathrm{got},\:\:\:\:\:\:\mathrm{411825205639}.\mathrm{48001}\:\: \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 20/Feb/19

Commented by tanmay.chaudhury50@gmail.com last updated on 20/Feb/19
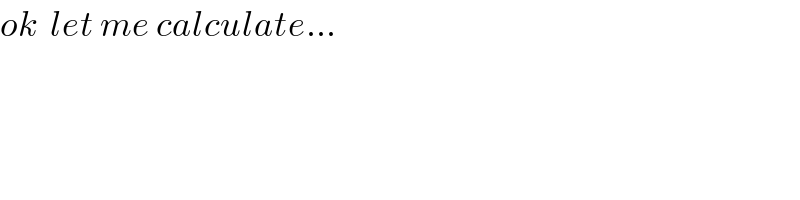
$${ok}\:\:{let}\:{me}\:{calculate}… \\ $$
Commented by Tawa1 last updated on 20/Feb/19

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Commented by Tawa1 last updated on 20/Feb/19
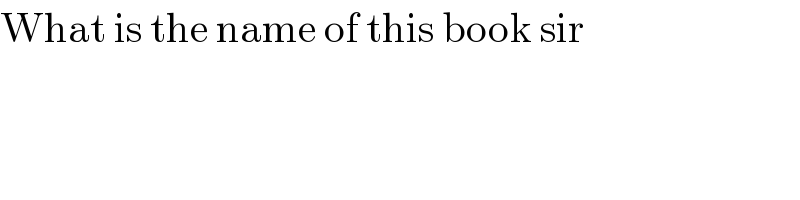
$$\mathrm{What}\:\mathrm{is}\:\mathrm{the}\:\mathrm{name}\:\mathrm{of}\:\mathrm{this}\:\mathrm{book}\:\mathrm{sir} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 20/Feb/19

Commented by Tawa1 last updated on 20/Feb/19
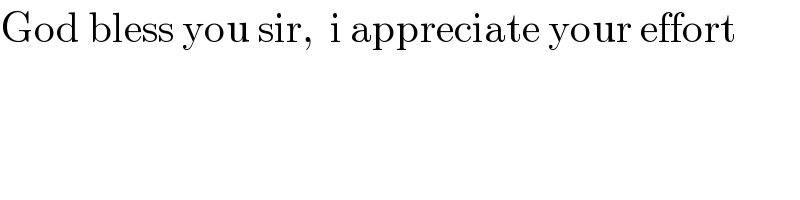
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir},\:\:\mathrm{i}\:\mathrm{appreciate}\:\mathrm{your}\:\mathrm{effort} \\ $$
