Question Number 55288 by peter frank last updated on 20/Feb/19

Answered by tanmay.chaudhury50@gmail.com last updated on 20/Feb/19
![F=[MLT^(−2) ] A=[L^2 ] ρ=[ML^(−3) ] V=[LT^(−1) ] k=numifical constant F=kAρV^α MLT^(−2) =k×L^2 ×ML^(−3) ×L^α T^(−α) MLT^(−2) =kML^(2+α−3) T^(−α) α−1=1 α=2→(comparing power of L) T^(−2) =T^(−α) so α=2 so α=2](https://www.tinkutara.com/question/Q55292.png)
$${F}=\left[{MLT}^{−\mathrm{2}} \right]\:\:\:{A}=\left[{L}^{\mathrm{2}} \right]\:\:\:\:\rho=\left[{ML}^{−\mathrm{3}} \right]\:\:\:{V}=\left[{LT}^{−\mathrm{1}} \right] \\ $$$$ \\ $$$${k}={numifical}\:{constant} \\ $$$${F}={kA}\rho{V}^{\alpha} \\ $$$${MLT}^{−\mathrm{2}} ={k}×{L}^{\mathrm{2}} ×{ML}^{−\mathrm{3}} ×{L}^{\alpha} {T}^{−\alpha} \\ $$$${MLT}^{−\mathrm{2}} ={kML}^{\mathrm{2}+\alpha−\mathrm{3}} {T}^{−\alpha} \\ $$$$\alpha−\mathrm{1}=\mathrm{1}\:\:\:\alpha=\mathrm{2}\rightarrow\left({comparing}\:{power}\:{of}\:{L}\right) \\ $$$${T}^{−\mathrm{2}} ={T}^{−\alpha} \:\:\:{so}\:\alpha=\mathrm{2} \\ $$$${so}\:\:\alpha=\mathrm{2} \\ $$$$ \\ $$$$ \\ $$
Commented by peter frank last updated on 20/Feb/19

$$\mathrm{thank}\:\mathrm{you} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 20/Feb/19
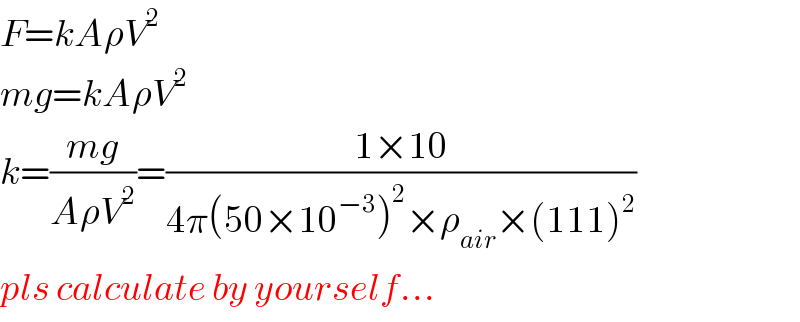
$${F}={kA}\rho{V}^{\mathrm{2}} \\ $$$${mg}={kA}\rho{V}^{\mathrm{2}} \\ $$$${k}=\frac{{mg}}{{A}\rho{V}^{\mathrm{2}} }=\frac{\mathrm{1}×\mathrm{10}}{\mathrm{4}\pi\left(\mathrm{50}×\mathrm{10}^{−\mathrm{3}} \right)^{\mathrm{2}} ×\rho_{{air}} ×\left(\mathrm{111}\right)^{\mathrm{2}} } \\ $$$${pls}\:{calculate}\:{by}\:{yourself}… \\ $$
