Question Number 55308 by Tawa1 last updated on 21/Feb/19

Answered by Rio Mike last updated on 21/Feb/19
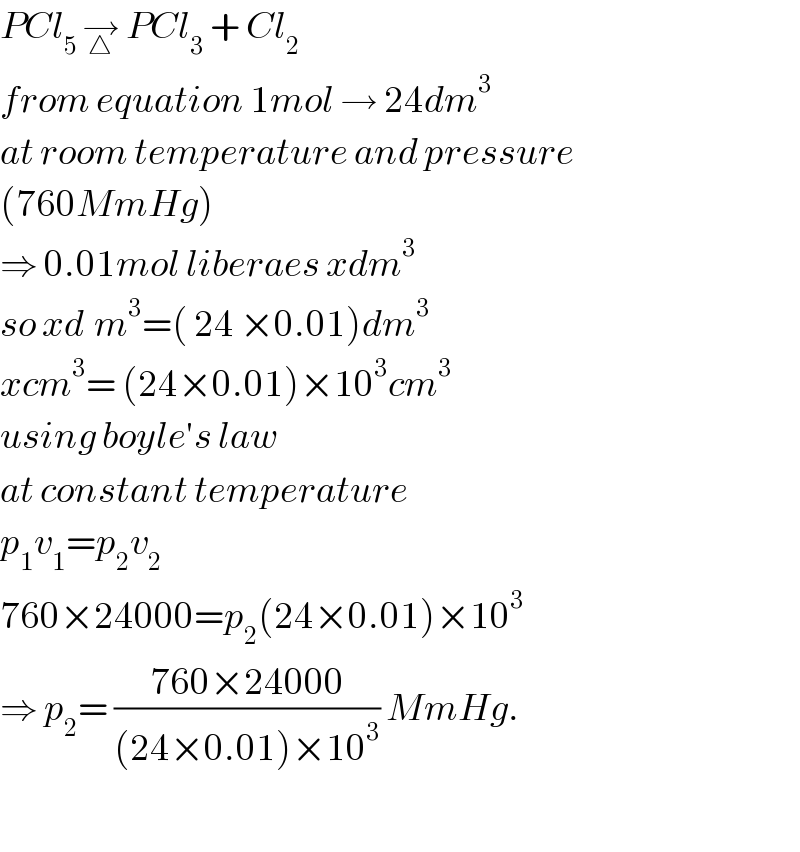
$${PCl}_{\mathrm{5}\:} \underset{\bigtriangleup} {\rightarrow}\:{PCl}_{\mathrm{3}} \:+\:{Cl}_{\mathrm{2}} \\ $$$${from}\:{equation}\:\mathrm{1}{mol}\:\rightarrow\:\mathrm{24}{dm}^{\mathrm{3}} \\ $$$${at}\:{room}\:{temperature}\:{and}\:{pressure} \\ $$$$\left(\mathrm{760}{MmHg}\right) \\ $$$$\Rightarrow\:\mathrm{0}.\mathrm{01}{mol}\:{liberaes}\:{xdm}^{\mathrm{3}} \\ $$$${so}\:{xd}^{} {m}^{\mathrm{3}} =\left(\:\mathrm{24}\:×\mathrm{0}.\mathrm{01}\right){dm}^{\mathrm{3}} \\ $$$${xcm}^{\mathrm{3}} =\:\left(\mathrm{24}×\mathrm{0}.\mathrm{01}\right)×\mathrm{10}^{\mathrm{3}} {cm}^{\mathrm{3}} \\ $$$${using}\:{boyle}'{s}\:{law}\: \\ $$$${at}\:{constant}\:{temperature} \\ $$$${p}_{\mathrm{1}} {v}_{\mathrm{1}} ={p}_{\mathrm{2}} {v}_{\mathrm{2}} \\ $$$$\mathrm{760}×\mathrm{24000}={p}_{\mathrm{2}} \left(\mathrm{24}×\mathrm{0}.\mathrm{01}\right)×\mathrm{10}^{\mathrm{3}} \\ $$$$\Rightarrow\:{p}_{\mathrm{2}} =\:\frac{\mathrm{760}×\mathrm{24000}}{\left(\mathrm{24}×\mathrm{0}.\mathrm{01}\right)×\mathrm{10}^{\mathrm{3}} }\:{MmHg}. \\ $$$$ \\ $$
Commented by Tawa1 last updated on 23/Feb/19
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
