Question Number 55362 by Hassen_Timol last updated on 22/Feb/19

Commented by tanmay.chaudhury50@gmail.com last updated on 22/Feb/19

$${pls}\:{check}\:\:\:{the}\:{sentence}\:{moving}\:\mathrm{30}^{{o}} \:{east}\:{etc} \\ $$
Answered by mr W last updated on 23/Feb/19
Commented by mr W last updated on 23/Feb/19

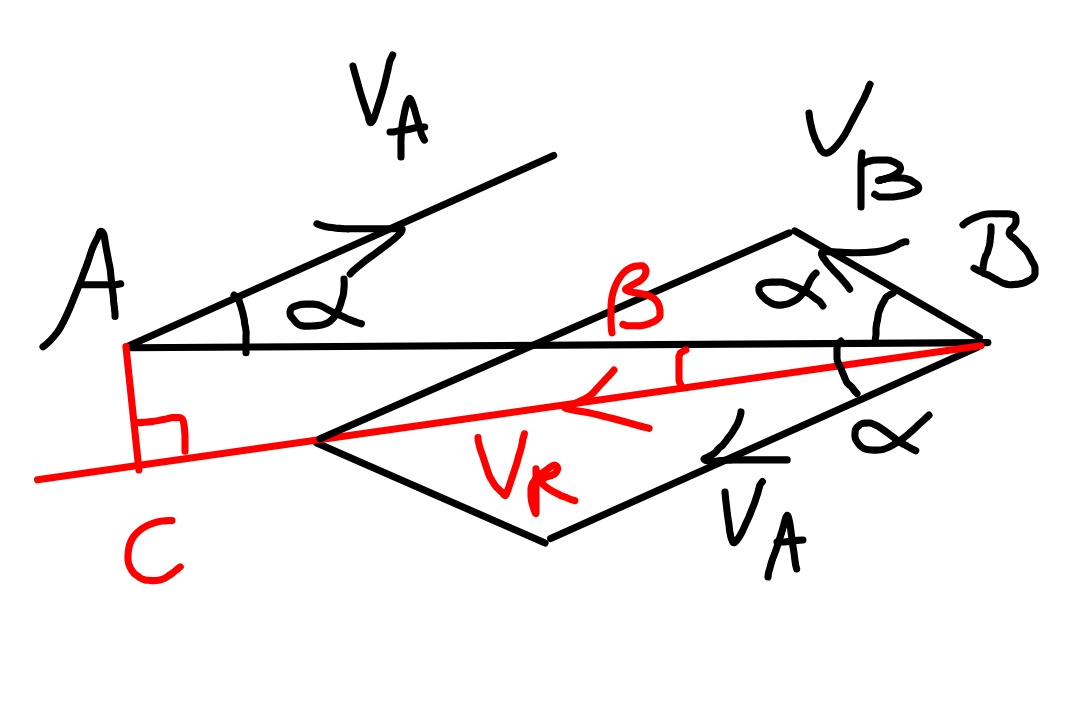
$${B}\:{moves}\:{relatively}\:{to}\:{A}\:{along}\:{path}\:{BC} \\ $$$${with}\:{relative}\:{speed}\:{v}_{{R}} . \\ $$$${v}_{{R}} =\sqrt{\left({v}_{{A}} +{v}_{{B}} \right)^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \:\mathrm{30}°+\left({v}_{{A}} −{v}_{{B}} \right)^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\mathrm{30}°} \\ $$$$=\sqrt{\left(\mathrm{20}+\mathrm{10}\right)^{\mathrm{2}} ×\frac{\mathrm{3}}{\mathrm{4}}+\left(\mathrm{20}−\mathrm{10}\right)^{\mathrm{2}} ×\frac{\mathrm{1}}{\mathrm{4}}} \\ $$$$=\mathrm{26}.\mathrm{457}\:{km}/{h} \\ $$$$\mathrm{tan}\:\beta=\frac{\left(\mathrm{20}−\mathrm{10}\right)×\mathrm{sin}\:\mathrm{30}°}{\left(\mathrm{20}+\mathrm{10}\right)×\mathrm{cos}\:\mathrm{30}°}=\frac{\mathrm{1}}{\mathrm{3}}×\mathrm{tan}\:\mathrm{30}° \\ $$$$\Rightarrow\beta=\mathrm{10}.\mathrm{893}° \\ $$$$ \\ $$$${closest}\:{distance}\:{from}\:{A}\:{and}\:{B}\:{is} \\ $$$${d}=\mathrm{40}×\mathrm{sin}\:\beta=\mathrm{7}.\mathrm{559}\:{km} \\ $$$$ \\ $$$${time}\:{to}\:{reach}\:{the}\:{closest}\:{point}\:{is} \\ $$$${t}=\frac{\mathrm{40}\:\mathrm{cos}\:\beta}{{v}_{{R}} }=\mathrm{1}.\mathrm{485}\:{h} \\ $$
Commented by Hassen_Timol last updated on 23/Feb/19
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{Sir} \\ $$$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you} \\ $$
Answered by mr W last updated on 23/Feb/19
Commented by mr W last updated on 23/Feb/19
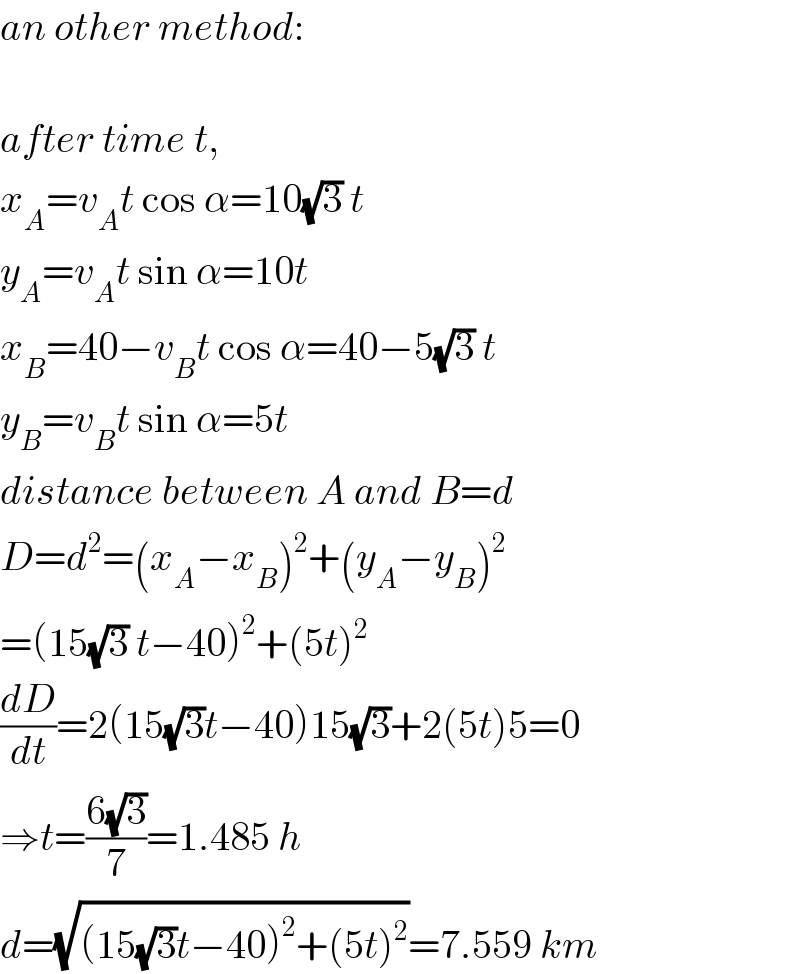
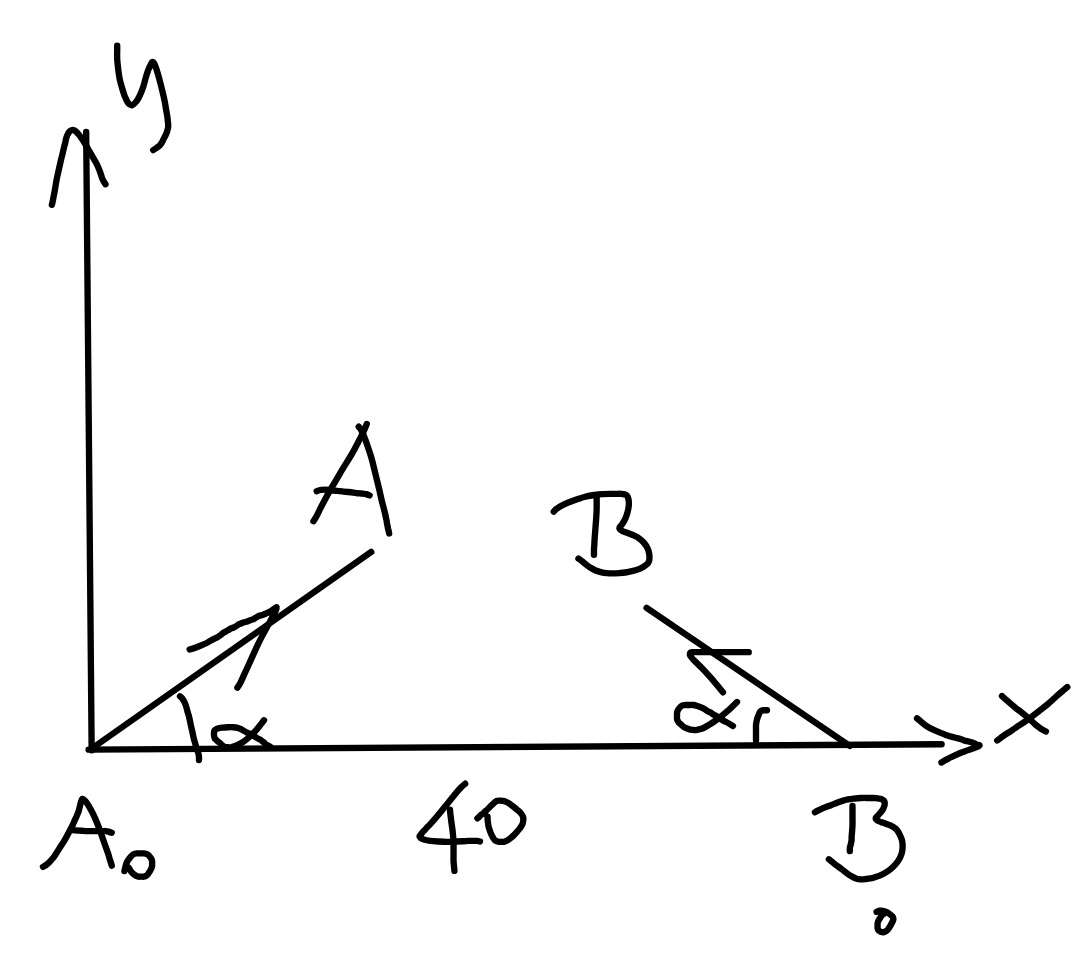
$${an}\:{other}\:{method}: \\ $$$$ \\ $$$${after}\:{time}\:{t}, \\ $$$${x}_{{A}} ={v}_{{A}} {t}\:\mathrm{cos}\:\alpha=\mathrm{10}\sqrt{\mathrm{3}}\:{t} \\ $$$${y}_{{A}} ={v}_{{A}} {t}\:\mathrm{sin}\:\alpha=\mathrm{10}{t} \\ $$$${x}_{{B}} =\mathrm{40}−{v}_{{B}} {t}\:\mathrm{cos}\:\alpha=\mathrm{40}−\mathrm{5}\sqrt{\mathrm{3}}\:{t} \\ $$$${y}_{{B}} ={v}_{{B}} {t}\:\mathrm{sin}\:\alpha=\mathrm{5}{t} \\ $$$${distance}\:{between}\:{A}\:{and}\:{B}={d} \\ $$$${D}={d}^{\mathrm{2}} =\left({x}_{{A}} −{x}_{{B}} \right)^{\mathrm{2}} +\left({y}_{{A}} −{y}_{{B}} \right)^{\mathrm{2}} \\ $$$$=\left(\mathrm{15}\sqrt{\mathrm{3}}\:{t}−\mathrm{40}\right)^{\mathrm{2}} +\left(\mathrm{5}{t}\right)^{\mathrm{2}} \\ $$$$\frac{{dD}}{{dt}}=\mathrm{2}\left(\mathrm{15}\sqrt{\mathrm{3}}{t}−\mathrm{40}\right)\mathrm{15}\sqrt{\mathrm{3}}+\mathrm{2}\left(\mathrm{5}{t}\right)\mathrm{5}=\mathrm{0} \\ $$$$\Rightarrow{t}=\frac{\mathrm{6}\sqrt{\mathrm{3}}}{\mathrm{7}}=\mathrm{1}.\mathrm{485}\:{h} \\ $$$${d}=\sqrt{\left(\mathrm{15}\sqrt{\mathrm{3}}{t}−\mathrm{40}\right)^{\mathrm{2}} +\left(\mathrm{5}{t}\right)^{\mathrm{2}} }=\mathrm{7}.\mathrm{559}\:{km} \\ $$
Commented by Hassen_Timol last updated on 18/Mar/19

$${Sorry}\:{Sir}…\:{Can}\:{you}\:{explain}\:{me}\:{the}\:{method} \\ $$$${I}'{m}\:{not}\:{sure}\:{to}\:{have}\:{understand}\:{it}\:{entirely}\:? \\ $$
