Question Number 55539 by mr W last updated on 26/Feb/19
Commented by MJS last updated on 27/Feb/19
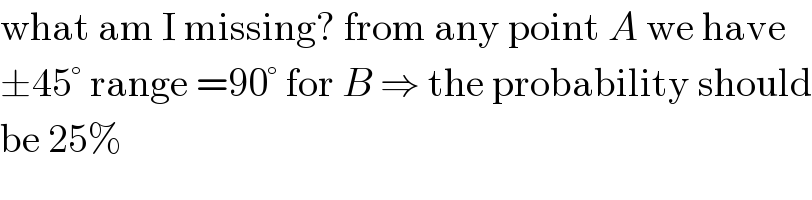
$$\mathrm{what}\:\mathrm{am}\:\mathrm{I}\:\mathrm{missing}?\:\mathrm{from}\:\mathrm{any}\:\mathrm{point}\:{A}\:\mathrm{we}\:\mathrm{have} \\ $$$$\pm\mathrm{45}°\:\mathrm{range}\:=\mathrm{90}°\:\mathrm{for}\:{B}\:\Rightarrow\:\mathrm{the}\:\mathrm{probability}\:\mathrm{should} \\ $$$$\mathrm{be}\:\mathrm{25\%} \\ $$
Commented by mr W last updated on 26/Feb/19
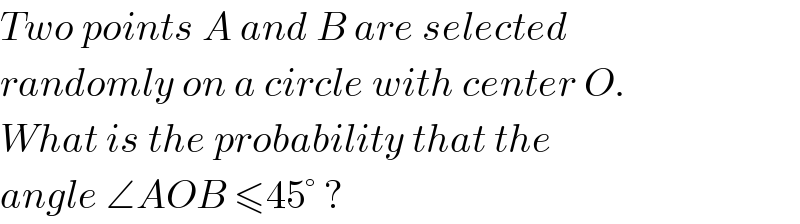
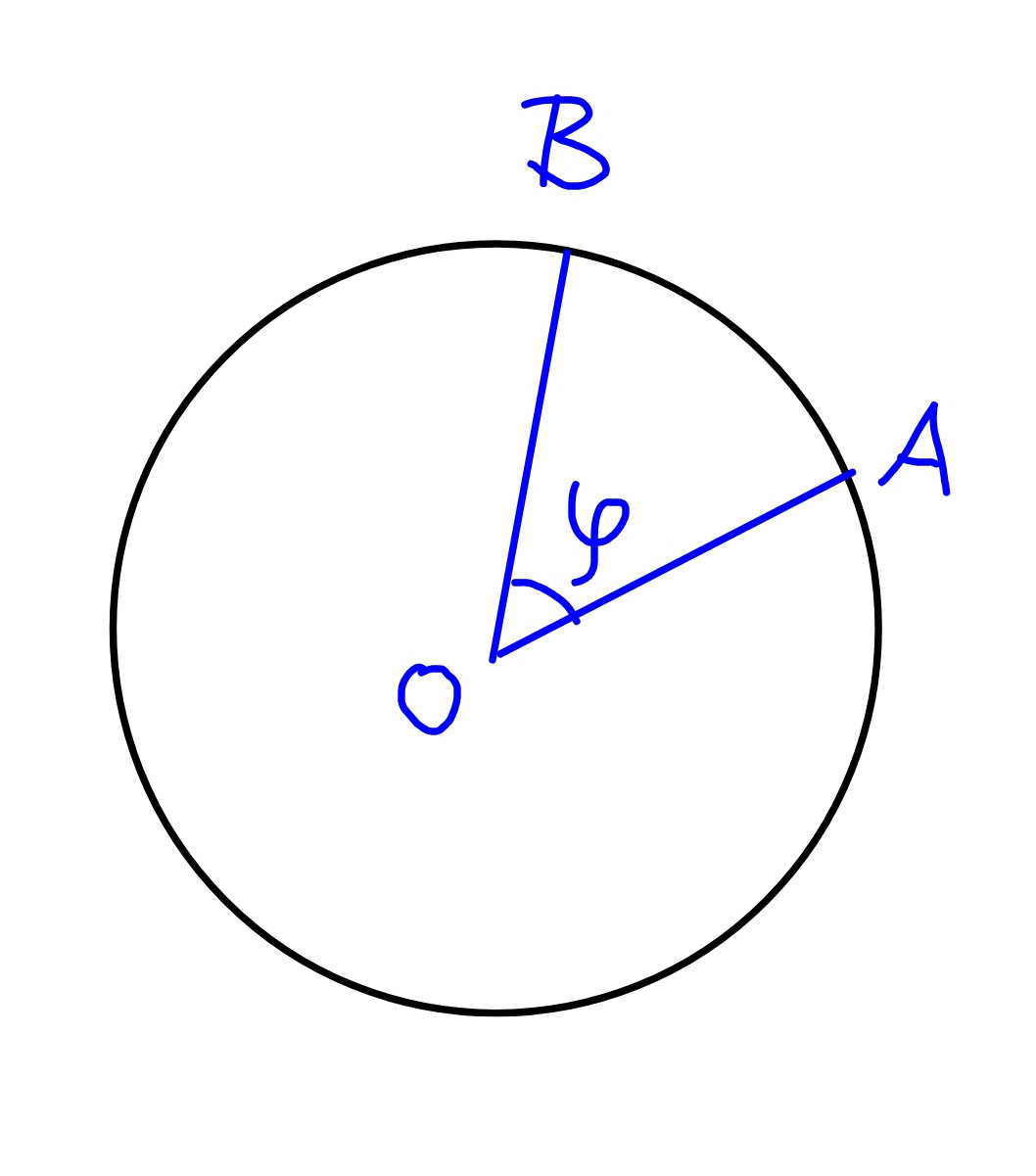
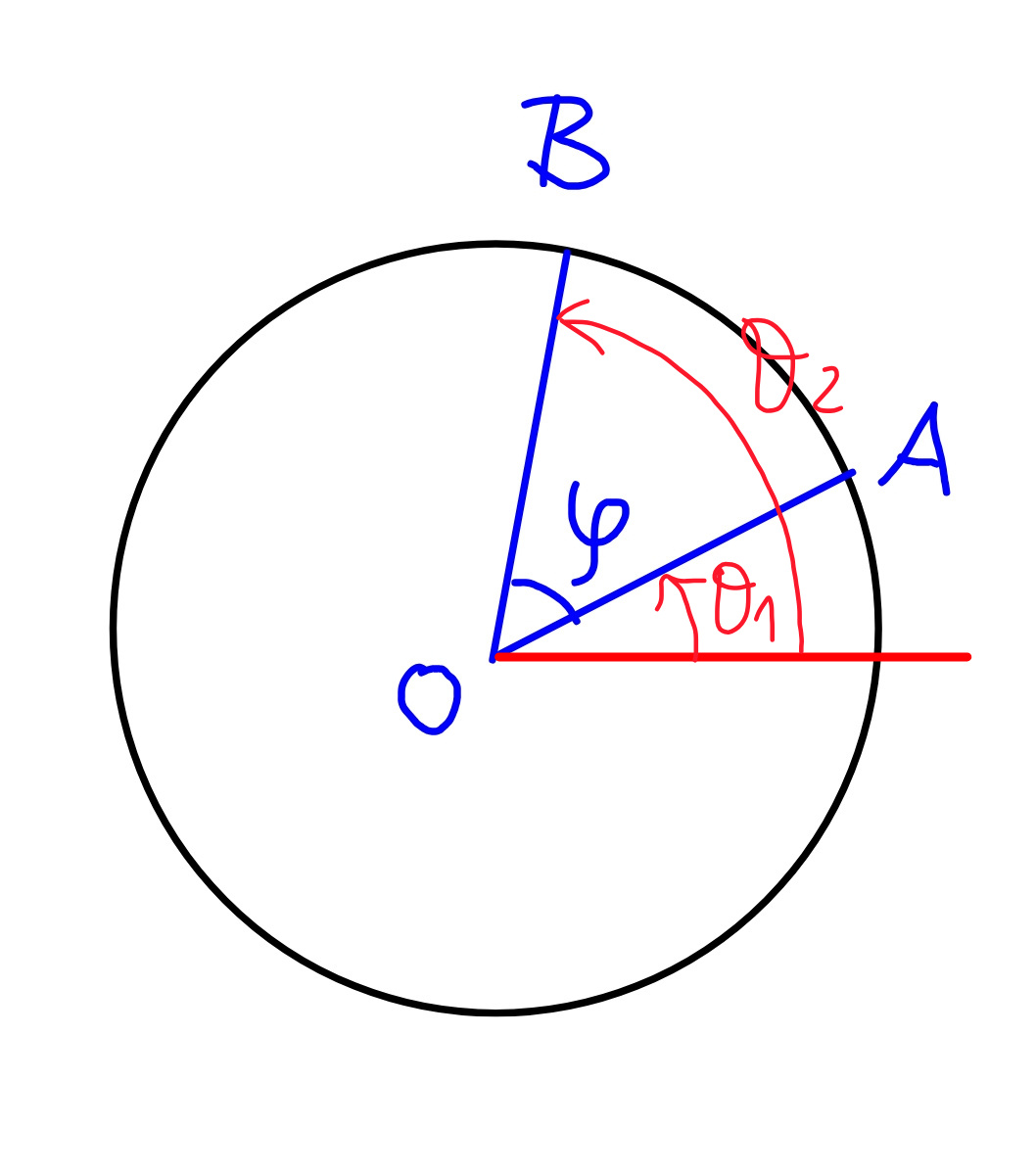
$${Two}\:{points}\:{A}\:{and}\:{B}\:{are}\:{selected} \\ $$$${randomly}\:{on}\:{a}\:{circle}\:{with}\:{center}\:{O}. \\ $$$${What}\:{is}\:{the}\:{probability}\:{that}\:{the} \\ $$$${angle}\:\angle{AOB}\:\leqslant\mathrm{45}°\:? \\ $$
Answered by kaivan.ahmadi last updated on 26/Feb/19
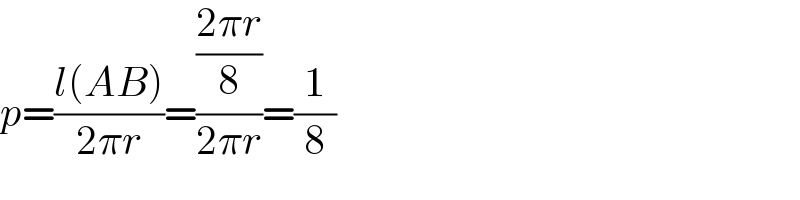
$${p}=\frac{{l}\left({AB}\right)}{\mathrm{2}\pi{r}}=\frac{\frac{\mathrm{2}\pi{r}}{\mathrm{8}}}{\mathrm{2}\pi{r}}=\frac{\mathrm{1}}{\mathrm{8}} \\ $$
Answered by mr W last updated on 26/Feb/19
Commented by MJS last updated on 27/Feb/19
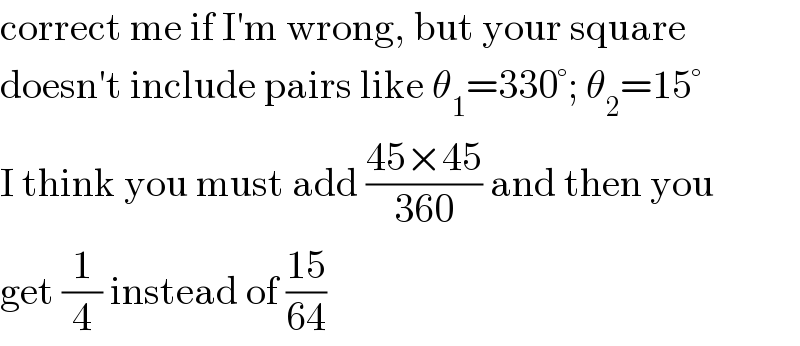
$$\mathrm{correct}\:\mathrm{me}\:\mathrm{if}\:\mathrm{I}'\mathrm{m}\:\mathrm{wrong},\:\mathrm{but}\:\mathrm{your}\:\mathrm{square} \\ $$$$\mathrm{doesn}'\mathrm{t}\:\mathrm{include}\:\mathrm{pairs}\:\mathrm{like}\:\theta_{\mathrm{1}} =\mathrm{330}°;\:\theta_{\mathrm{2}} =\mathrm{15}° \\ $$$$\mathrm{I}\:\mathrm{think}\:\mathrm{you}\:\mathrm{must}\:\mathrm{add}\:\frac{\mathrm{45}×\mathrm{45}}{\mathrm{360}}\:\mathrm{and}\:\mathrm{then}\:\mathrm{you} \\ $$$$\mathrm{get}\:\frac{\mathrm{1}}{\mathrm{4}}\:\mathrm{instead}\:\mathrm{of}\:\frac{\mathrm{15}}{\mathrm{64}} \\ $$
Commented by mr W last updated on 26/Feb/19

$${the}\:{position}\:{of}\:{A}\:{can}\:{be}\:{represented} \\ $$$${by}\:\theta_{\mathrm{1}} \:{with}\:\theta_{\mathrm{1}} \:{uniformly}\:{distributed}\: \\ $$$${between}\:\mathrm{0}\:{and}\:\mathrm{360}°. \\ $$$${the}\:{position}\:{of}\:{B}\:{can}\:{be}\:{represented} \\ $$$${by}\:\theta_{\mathrm{2}} \:{with}\:\theta_{\mathrm{2}} \:{uniformly}\:{distributed}\: \\ $$$${between}\:\mathrm{0}\:{and}\:\mathrm{360}°. \\ $$$$\varphi=\theta_{\mathrm{2}} −\theta_{\mathrm{1}} \\ $$$$−\mathrm{45}°\leqslant\varphi\leqslant\mathrm{45}° \\ $$$$\Rightarrow−\mathrm{45}°\leqslant\theta_{\mathrm{2}} −\theta_{\mathrm{1}} \leqslant\mathrm{45}° \\ $$$$\Rightarrow\theta_{\mathrm{2}} −\theta_{\mathrm{1}} \geqslant−\mathrm{45}° \\ $$$$\Rightarrow\theta_{\mathrm{2}} −\theta_{\mathrm{1}} \leqslant\mathrm{45}° \\ $$
Commented by mr W last updated on 26/Feb/19
Commented by mr W last updated on 26/Feb/19

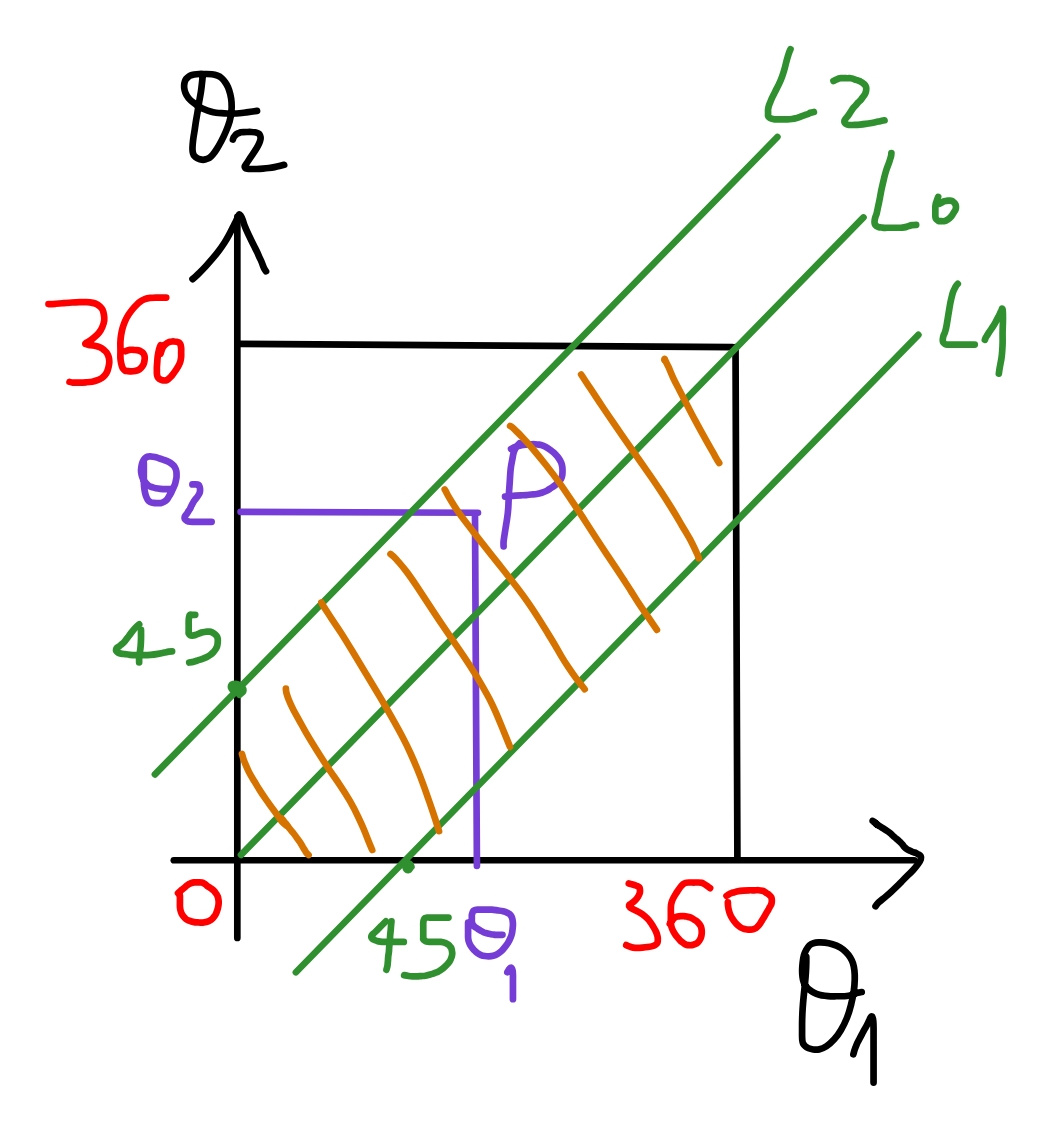
$${each}\:{point}\:{P}\:{in}\:{the}\:{square}\:\mathrm{360}×\mathrm{360} \\ $$$${represents}\:{a}\:{point}\:{pair}\:{A}\:{and}\:{B}.\: \\ $$$${the}\:{area}\:{of}\:{square}\:\mathrm{360}×\mathrm{360}\:{represents} \\ $$$${all}\:{possibilities}. \\ $$$${line}\:{L}_{\mathrm{1}} :\:\theta_{\mathrm{2}} −\theta_{\mathrm{1}} =−\mathrm{45}° \\ $$$${line}\:{L}_{\mathrm{2}} :\:\theta_{\mathrm{2}} −\theta_{\mathrm{1}} =\mathrm{45}° \\ $$$${it}\:{means}\:{each}\:{point}\:{in}\:{the}\:{shaded} \\ $$$${area}\:{fulfills}\:{the}\:{condition} \\ $$$$−\mathrm{45}°\leqslant\theta_{\mathrm{2}} −\theta_{\mathrm{1}} \leqslant\mathrm{45}° \\ $$$${therefore}\:{the}\:{probability}\:{for}\:\mid\varphi\mid\leqslant\mathrm{45}° \\ $$$${is}\:{p}=\frac{{area}\:{shaded}}{{area}\:{of}\:{square}}=\frac{\mathrm{360}×\mathrm{360}−\mathrm{315}×\mathrm{315}}{\mathrm{360}×\mathrm{360}} \\ $$$${which}\:{is}\:\frac{\mathrm{15}}{\mathrm{64}}\approx\mathrm{0}.\mathrm{234}. \\ $$
Commented by kaivan.ahmadi last updated on 26/Feb/19

$${it}\:{is}\:{equvalent}\:{to}: \\ $$$${if}\:{we}\:{have}\:{a}\:{line}\:{segment}\:{with}\:{length}\:\mathrm{2}\pi{r} \\ $$$${and}\:{we}\:{chose}\:{tow}\:{poin}\:{A},{B} \\ $$$${what}\:{is}\:{the}\:{probablity}\:{that}\:{A}\overset{−} {{B}}\leqslant\frac{\pi{r}}{\mathrm{4}} \\ $$
Commented by mr W last updated on 26/Feb/19
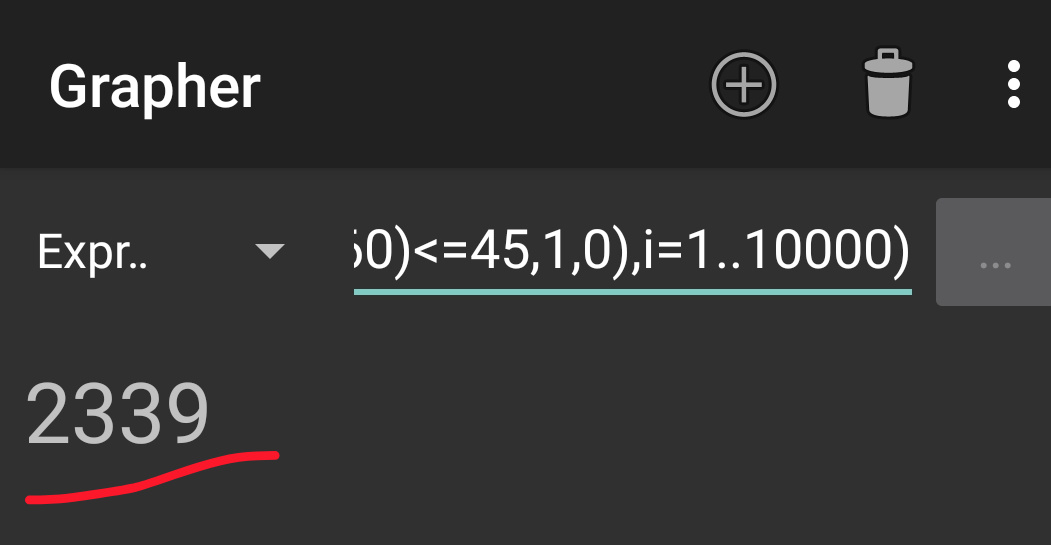
I tried to simulate this question with the app Grapher and got following result:
Among 10000 random selections 2339 fulfill the condiction, the probability is 0.2339.
This is what I input:
sum(if(abs(rnd*360-rnd*360)<=45,1,0),i=1..10000)
Commented by mr W last updated on 26/Feb/19
Commented by mr W last updated on 26/Feb/19
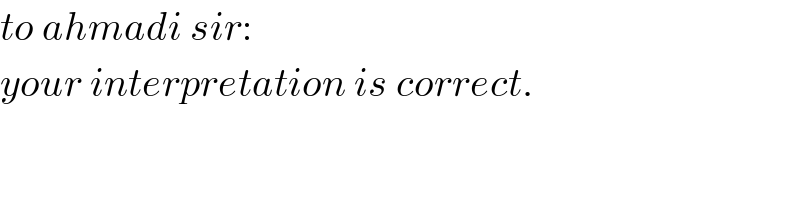
$${to}\:{ahmadi}\:{sir}:\: \\ $$$${your}\:{interpretation}\:{is}\:{correct}. \\ $$
Commented by kaivan.ahmadi last updated on 26/Feb/19
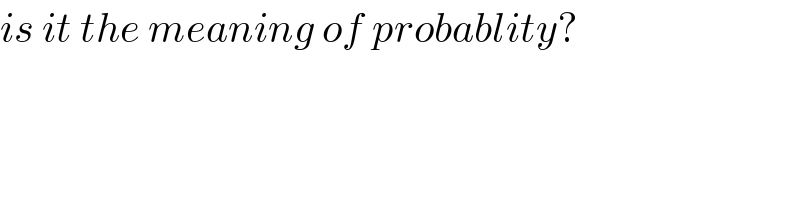
$${is}\:{it}\:{the}\:{meaning}\:{of}\:{probablity}? \\ $$
Commented by mr W last updated on 26/Feb/19

$${yes}. \\ $$
Commented by mr W last updated on 27/Feb/19
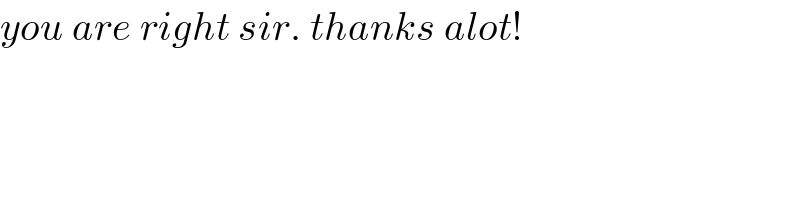
$${you}\:{are}\:{right}\:{sir}.\:{thanks}\:{alot}! \\ $$
