Menu Close

Question-55577

Tinku Tara 0 Comments
Pin




Question Number 55577 by rahul 19 last updated on 27/Feb/19
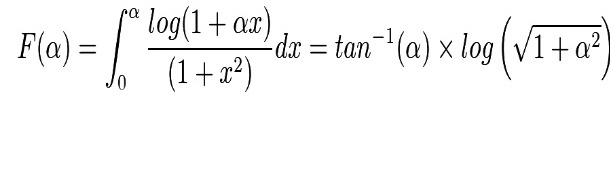
Commented by rahul 19 last updated on 27/Feb/19
Prove that:
$${Prove}\:{that}: \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 27/Feb/19
(dF/dα)=∫(∂/∂α)(((ln(1+αx))/(1+x^2 )))dx+((ln(1+α^2 ))/(1+α^2 ))×(dα/dα)−((ln(1+α×0))/(1+0^2 ))×(d/dα)(0) =∫_0 ^α (1/(1+x^2 ))×(1/(1+αx))×x dx+((ln(1+α^2 ))/(1+α^2 )) =∫_0 ^α (x/((1+x^2 )(1+αx)))dx+((ln(1+α^2 ))/(1+α^2 )) now (x/((1+x^2 )(1+αx)))=((ax+b)/(1+x^2 ))+(c/(1+αx)) x=(ax+b)(1+αx)+c+cx^2 x=ax+aαx^2 +b+bαx+c+cx^2 x=x^2 (aα+c)+x(a+bα)+b+c aα+c=0 a+bα=1 b+c=0 aα−b=0 a+bα=1 a+aα^2 =1 a=(1/(1+α^2 )) b=(α/(1+α^2 )) c=((−α)/(1+α^2 )) ∫_0 ^α (((ax+b)/(1+x^2 ))+(c/(1+αx)))dx (1/(2(1+α^2 )))∫_0 ^α ((2x)/(1+x^2 ))+(α/(1+α^2 ))∫_0 ^α (dx/(1+x^2 ))+((−α)/(1+α^2 ))∫(dx/(1+αx)) (1/(2(1+α^2 )))∫_0 ^α ((d(1+x^2 ))/(1+x^2 ))+(α/(1+α^2 ))∫_0 ^α (dx/(1+x^2 ))+((−α)/(1+α^2 ))∫_0 ^α (dx/(1+αx)) ∣(1/(2(1+α^2 )))ln(1+x^2 )+(α/(1+α^2 ))tan^(−1) (x)+((−α)/(1+α^2 ))×((ln(1+αx))/α)∣_0 ^α (1/(2(1+α^2 )))×ln(1+α^2 )+(α/(1+α^2 ))tan^(−1) (α)+((−1)/(1+α^2 ))×ln(1+α^2 ) =(α/(1+α^2 ))tan^(−1) (α)−(1/(2(1+α^2 )))×ln(1+α^2 ) so (dF/dα)=(α/(1+α^2 ))tan^(−1) (α)+((ln(1+α^2 ))/(2(1+α^2 ))) wait pls =tan^(−1) (α)(d/dα){ln(√(1+α^2 )) }+ln{(√(1+α^2 )) ×(d/dα)tan^(−1) α} =(d/dα){tan^(−1) α×ln(√(1+α^2 )) } so F=tan^(−1) (α)×ln(√(1+α^2 )) proved
$$\frac{{dF}}{{d}\alpha}=\int\frac{\partial}{\partial\alpha}\left(\frac{{ln}\left(\mathrm{1}+\alpha{x}\right)}{\mathrm{1}+{x}^{\mathrm{2}} }\right){dx}+\frac{{ln}\left(\mathrm{1}+\alpha^{\mathrm{2}} \right)}{\mathrm{1}+\alpha^{\mathrm{2}} }×\frac{{d}\alpha}{{d}\alpha}−\frac{{ln}\left(\mathrm{1}+\alpha×\mathrm{0}\right)}{\mathrm{1}+\mathrm{0}^{\mathrm{2}} }×\frac{{d}}{{d}\alpha}\left(\mathrm{0}\right) \\ $$$$=\int_{\mathrm{0}} ^{\alpha} \frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} }×\frac{\mathrm{1}}{\mathrm{1}+\alpha{x}}×{x}\:{dx}+\frac{{ln}\left(\mathrm{1}+\alpha^{\mathrm{2}} \right)}{\mathrm{1}+\alpha^{\mathrm{2}} } \\ $$$$=\int_{\mathrm{0}} ^{\alpha} \frac{{x}}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\left(\mathrm{1}+\alpha{x}\right)}{dx}+\frac{{ln}\left(\mathrm{1}+\alpha^{\mathrm{2}} \right)}{\mathrm{1}+\alpha^{\mathrm{2}} } \\ $$$${now}\: \\ $$$$\frac{{x}}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\left(\mathrm{1}+\alpha{x}\right)}=\frac{{ax}+{b}}{\mathrm{1}+{x}^{\mathrm{2}} }+\frac{{c}}{\mathrm{1}+\alpha{x}} \\ $$$${x}=\left({ax}+{b}\right)\left(\mathrm{1}+\alpha{x}\right)+{c}+{cx}^{\mathrm{2}} \\ $$$${x}={ax}+{a}\alpha{x}^{\mathrm{2}} +{b}+{b}\alpha{x}+{c}+{cx}^{\mathrm{2}} \\ $$$${x}={x}^{\mathrm{2}} \left({a}\alpha+{c}\right)+{x}\left({a}+{b}\alpha\right)+{b}+{c} \\ $$$${a}\alpha+{c}=\mathrm{0} \\ $$$${a}+{b}\alpha=\mathrm{1} \\ $$$${b}+{c}=\mathrm{0} \\ $$$${a}\alpha−{b}=\mathrm{0} \\ $$$${a}+{b}\alpha=\mathrm{1} \\ $$$${a}+{a}\alpha^{\mathrm{2}} =\mathrm{1} \\ $$$${a}=\frac{\mathrm{1}}{\mathrm{1}+\alpha^{\mathrm{2}} }\:\:\:{b}=\frac{\alpha}{\mathrm{1}+\alpha^{\mathrm{2}} }\:\:{c}=\frac{−\alpha}{\mathrm{1}+\alpha^{\mathrm{2}} } \\ $$$$\int_{\mathrm{0}} ^{\alpha} \left(\frac{{ax}+{b}}{\mathrm{1}+{x}^{\mathrm{2}} }+\frac{{c}}{\mathrm{1}+\alpha{x}}\right){dx} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{1}+\alpha^{\mathrm{2}} \right)}\int_{\mathrm{0}} ^{\alpha} \frac{\mathrm{2}{x}}{\mathrm{1}+{x}^{\mathrm{2}} }+\frac{\alpha}{\mathrm{1}+\alpha^{\mathrm{2}} }\int_{\mathrm{0}} ^{\alpha} \frac{{dx}}{\mathrm{1}+{x}^{\mathrm{2}} }+\frac{−\alpha}{\mathrm{1}+\alpha^{\mathrm{2}} }\int\frac{{dx}}{\mathrm{1}+\alpha{x}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{1}+\alpha^{\mathrm{2}} \right)}\int_{\mathrm{0}} ^{\alpha} \frac{{d}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}{\mathrm{1}+{x}^{\mathrm{2}} }+\frac{\alpha}{\mathrm{1}+\alpha^{\mathrm{2}} }\int_{\mathrm{0}} ^{\alpha} \frac{{dx}}{\mathrm{1}+{x}^{\mathrm{2}} }+\frac{−\alpha}{\mathrm{1}+\alpha^{\mathrm{2}} }\int_{\mathrm{0}} ^{\alpha} \frac{{dx}}{\mathrm{1}+\alpha{x}} \\ $$$$\mid\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{1}+\alpha^{\mathrm{2}} \right)}{ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)+\frac{\alpha}{\mathrm{1}+\alpha^{\mathrm{2}} }{tan}^{−\mathrm{1}} \left({x}\right)+\frac{−\alpha}{\mathrm{1}+\alpha^{\mathrm{2}} }×\frac{{ln}\left(\mathrm{1}+\alpha{x}\right)}{\alpha}\mid_{\mathrm{0}} ^{\alpha} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{1}+\alpha^{\mathrm{2}} \right)}×{ln}\left(\mathrm{1}+\alpha^{\mathrm{2}} \right)+\frac{\alpha}{\mathrm{1}+\alpha^{\mathrm{2}} }{tan}^{−\mathrm{1}} \left(\alpha\right)+\frac{−\mathrm{1}}{\mathrm{1}+\alpha^{\mathrm{2}} }×{ln}\left(\mathrm{1}+\alpha^{\mathrm{2}} \right) \\ $$$$=\frac{\alpha}{\mathrm{1}+\alpha^{\mathrm{2}} }{tan}^{−\mathrm{1}} \left(\alpha\right)−\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{1}+\alpha^{\mathrm{2}} \right)}×{ln}\left(\mathrm{1}+\alpha^{\mathrm{2}} \right) \\ $$$${so} \\ $$$$\frac{{dF}}{{d}\alpha}=\frac{\alpha}{\mathrm{1}+\alpha^{\mathrm{2}} }{tan}^{−\mathrm{1}} \left(\alpha\right)+\frac{{ln}\left(\mathrm{1}+\alpha^{\mathrm{2}} \right)}{\mathrm{2}\left(\mathrm{1}+\alpha^{\mathrm{2}} \right)} \\ $$$${wait}\:{pls} \\ $$$$={tan}^{−\mathrm{1}} \left(\alpha\right)\frac{{d}}{{d}\alpha}\left\{{ln}\sqrt{\mathrm{1}+\alpha^{\mathrm{2}} }\:\right\}+{ln}\left\{\sqrt{\mathrm{1}+\alpha^{\mathrm{2}} }\:×\frac{{d}}{{d}\alpha}{tan}^{−\mathrm{1}} \alpha\right\} \\ $$$$=\frac{{d}}{{d}\alpha}\left\{{tan}^{−\mathrm{1}} \alpha×{ln}\sqrt{\mathrm{1}+\alpha^{\mathrm{2}} }\:\right\} \\ $$$${so}\:{F}={tan}^{−\mathrm{1}} \left(\alpha\right)×{ln}\sqrt{\mathrm{1}+\alpha^{\mathrm{2}} }\:{proved} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *