Question-55625

Question Number 55625 by gunawan last updated on 28/Feb/19

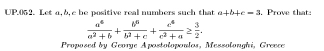
Commented by kaivan.ahmadi last updated on 28/Feb/19

$${the}\:{image}\:{is}\:{not}\:{clear} \\ $$

Commented by gunawan last updated on 28/Feb/19

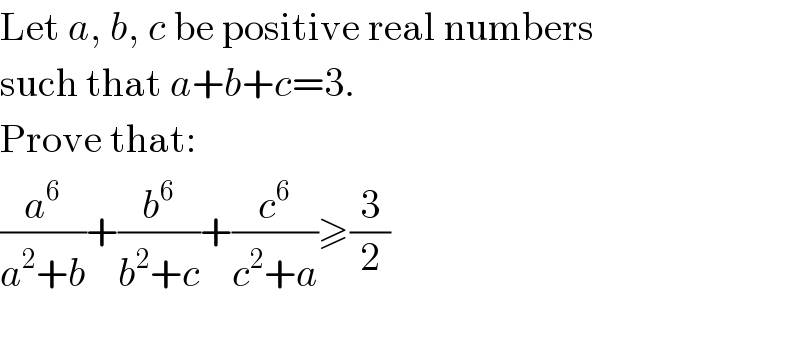
Let a, b, c be positive real numbers such that a+b+c=3. Prove that: (a^6 /(a^2 +b))+(b^6 /(b^2 +c))+(c^6 /(c^2 +a))≥(3/2)

$$\mathrm{Let}\:{a},\:{b},\:{c}\:\mathrm{be}\:\mathrm{positive}\:\mathrm{real}\:\mathrm{numbers} \\ $$$$\mathrm{such}\:\mathrm{that}\:{a}+{b}+{c}=\mathrm{3}. \\ $$$$\mathrm{Prove}\:\mathrm{that}: \\ $$$$\frac{{a}^{\mathrm{6}} }{{a}^{\mathrm{2}} +{b}}+\frac{{b}^{\mathrm{6}} }{{b}^{\mathrm{2}} +{c}}+\frac{{c}^{\mathrm{6}} }{{c}^{\mathrm{2}} +{a}}\geqslant\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$ \\ $$

Commented by tanmay.chaudhury50@gmail.com last updated on 03/Mar/19

((A+B)/2)≥(√(AB)) ≥((2AB)/(A+B)) (1/2)((a^2 /a^6 )+(b/a^6 ))≥(√((a^2 b)/(a^6 a^6 ))) ≥((2(a^2 /a^6 )×(b/a^6 ))/((a^2 /a^6 )+(b/a^6 ))) ((a^2 /a^6 )+(b/a^6 ))≥2×(√(b/a^(10) )) ((a^2 +b)/a^6 )≥((2(√b))/a^5 ) (a^6 /(a^2 +b))≤(a^5 /(2(√b))) given expression i,e p≤(a^5 /(2(√b)))+(b^5 /(2(√c)))+(c^5 /(2(√a))) let given expression (a^6 /(a^2 +b))+(b^6 /(b^2 +c))+(c^6 /(c^2 +a))=p (p/3)≤(1/3)((a^5 /(2(√b)))+(b^5 /(2(√c)))+(c^5 /(2(√a))))≥((a^5 /(2(√b)))×(b^5 /(2(√c)))×(c^5 /(2(√a))))^(1/3) (p/3)≤(1/3)((a^5 /(2(√b)))+(b^5 /(2(√c)))+(c^5 /(2(√a))))≥(1/2)(abc)^(9/2) (p/3)=(1/2) p=(3/2) since ((a+b+c)/3)≥(abc)^(1/3) (3/3)≥(abc)^(1/3) abc=1 (/)

$$\frac{\boldsymbol{{A}}+{B}}{\mathrm{2}}\geqslant\sqrt{{AB}}\:\geqslant\frac{\mathrm{2}{AB}}{{A}+{B}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{{a}^{\mathrm{2}} }{{a}^{\mathrm{6}} }+\frac{{b}}{{a}^{\mathrm{6}} }\right)\geqslant\sqrt{\frac{{a}^{\mathrm{2}} {b}}{{a}^{\mathrm{6}} {a}^{\mathrm{6}} }}\:\geqslant\frac{\mathrm{2}\frac{{a}^{\mathrm{2}} }{{a}^{\mathrm{6}} }×\frac{{b}}{{a}^{\mathrm{6}} }}{\frac{{a}^{\mathrm{2}} }{{a}^{\mathrm{6}} }+\frac{{b}}{{a}^{\mathrm{6}} }} \\ $$$$\left(\frac{{a}^{\mathrm{2}} }{{a}^{\mathrm{6}} }+\frac{{b}}{{a}^{\mathrm{6}} }\right)\geqslant\mathrm{2}×\sqrt{\frac{{b}}{{a}^{\mathrm{10}} }}\: \\ $$$$\frac{{a}^{\mathrm{2}} +{b}}{{a}^{\mathrm{6}} }\geqslant\frac{\mathrm{2}\sqrt{{b}}}{{a}^{\mathrm{5}} } \\ $$$$\frac{{a}^{\mathrm{6}} }{{a}^{\mathrm{2}} +{b}}\leqslant\frac{{a}^{\mathrm{5}} }{\mathrm{2}\sqrt{{b}}} \\ $$$${given}\:{expression}\:{i},{e}\:{p}\leqslant\frac{{a}^{\mathrm{5}} }{\mathrm{2}\sqrt{{b}}}+\frac{{b}^{\mathrm{5}} }{\mathrm{2}\sqrt{{c}}}+\frac{{c}^{\mathrm{5}} }{\mathrm{2}\sqrt{{a}}} \\ $$$${let}\:{given}\:{expression}\:\frac{{a}^{\mathrm{6}} }{{a}^{\mathrm{2}} +{b}}+\frac{{b}^{\mathrm{6}} }{{b}^{\mathrm{2}} +{c}}+\frac{{c}^{\mathrm{6}} }{{c}^{\mathrm{2}} +{a}}={p} \\ $$$$\frac{{p}}{\mathrm{3}}\leqslant\frac{\mathrm{1}}{\mathrm{3}}\left(\frac{{a}^{\mathrm{5}} }{\mathrm{2}\sqrt{{b}}}+\frac{{b}^{\mathrm{5}} }{\mathrm{2}\sqrt{{c}}}+\frac{{c}^{\mathrm{5}} }{\mathrm{2}\sqrt{{a}}}\right)\geqslant\left(\frac{{a}^{\mathrm{5}} }{\mathrm{2}\sqrt{{b}}}×\frac{{b}^{\mathrm{5}} }{\mathrm{2}\sqrt{{c}}}×\frac{{c}^{\mathrm{5}} }{\mathrm{2}\sqrt{{a}}}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \\ $$$$\frac{{p}}{\mathrm{3}}\leqslant\frac{\mathrm{1}}{\mathrm{3}}\left(\frac{{a}^{\mathrm{5}} }{\mathrm{2}\sqrt{{b}}}+\frac{{b}^{\mathrm{5}} }{\mathrm{2}\sqrt{{c}}}+\frac{{c}^{\mathrm{5}} }{\mathrm{2}\sqrt{{a}}}\right)\geqslant\frac{\mathrm{1}}{\mathrm{2}}\left({abc}\right)^{\frac{\mathrm{9}}{\mathrm{2}}} \\ $$$$\frac{{p}}{\mathrm{3}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${p}=\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$ \\ $$$$ \\ $$$${since} \\ $$$$\frac{{a}+{b}+{c}}{\mathrm{3}}\geqslant\left({abc}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \\ $$$$\frac{\mathrm{3}}{\mathrm{3}}\geqslant\left({abc}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \:\:{abc}=\mathrm{1} \\ $$$$\frac{}{} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply