Question Number 55631 by Tawa1 last updated on 28/Feb/19
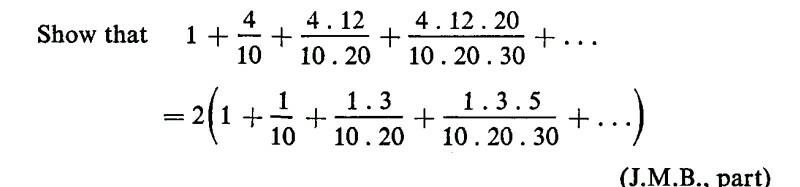
Answered by tanmay.chaudhury50@gmail.com last updated on 01/Mar/19
![(1−x)^((−1)/2) =1+(1/2)x+((1×3)/(2×4))x^2 +((1×3×5)/(2×4×6))x^3 +... LHS 1+(4/(10))+((4×12)/(10×20))+((4×12×20)/(10×20×30))+... =1+(1/2)((8/(10)))+((1×3)/(2×4))×(((4×4)/(5×5)))+((1×3×5)/(2×4×6))(((4×4×4)/(5×5×5)))+.. =1+(1/2)((4/5))+((1×3)/(2×4))×((4/5))^2 +((1×3×5)/(2×4×6))((4/5))^3 +.. =(1−(4/5))^((−1)/2) =((1/5))^((−1)/2) =(5^(−1) )^((−1)/2) =(5)^(1/2) =(√5) RHS 2(1+(1/(10))+((1.3)/(10.20))+((1.3.5)/(10.20.30))+...) =2(1+(1/2)×(1/(5 ))+((1×3)/(2×4))×(1/(5×5))+((1×3×5)/(2×4×6))×(1/(5×5×5))+..) =2[1+(1/2)((1/5))+((1×3)/(2×4))((1/5))^2 +((1×3×5)/(2×4×6))((1/5))^3 +...] =2[(1−(1/5))^((−1)/2) ] =2[((4/5))]^((−1)/2) =2×(4)^((−1)/2) ×((1/5))^((−1)/2) =2×2^(−1) ×(5^(−1) )^((−1)/2) =2×(1/2)×(5)^(1/2) =(5)^(1/2) =(√5) hence proved...](https://www.tinkutara.com/question/Q55656.png)
$$\left(\mathrm{1}−{x}\right)^{\frac{−\mathrm{1}}{\mathrm{2}}} \\ $$$$=\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}{x}+\frac{\mathrm{1}×\mathrm{3}}{\mathrm{2}×\mathrm{4}}{x}^{\mathrm{2}} +\frac{\mathrm{1}×\mathrm{3}×\mathrm{5}}{\mathrm{2}×\mathrm{4}×\mathrm{6}}{x}^{\mathrm{3}} +… \\ $$$$\boldsymbol{{L}}{HS} \\ $$$$\mathrm{1}+\frac{\mathrm{4}}{\mathrm{10}}+\frac{\mathrm{4}×\mathrm{12}}{\mathrm{10}×\mathrm{20}}+\frac{\mathrm{4}×\mathrm{12}×\mathrm{20}}{\mathrm{10}×\mathrm{20}×\mathrm{30}}+… \\ $$$$=\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{8}}{\mathrm{10}}\right)+\frac{\mathrm{1}×\mathrm{3}}{\mathrm{2}×\mathrm{4}}×\left(\frac{\mathrm{4}×\mathrm{4}}{\mathrm{5}×\mathrm{5}}\right)+\frac{\mathrm{1}×\mathrm{3}×\mathrm{5}}{\mathrm{2}×\mathrm{4}×\mathrm{6}}\left(\frac{\mathrm{4}×\mathrm{4}×\mathrm{4}}{\mathrm{5}×\mathrm{5}×\mathrm{5}}\right)+.. \\ $$$$=\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{4}}{\mathrm{5}}\right)+\frac{\mathrm{1}×\mathrm{3}}{\mathrm{2}×\mathrm{4}}×\left(\frac{\mathrm{4}}{\mathrm{5}}\right)^{\mathrm{2}} +\frac{\mathrm{1}×\mathrm{3}×\mathrm{5}}{\mathrm{2}×\mathrm{4}×\mathrm{6}}\left(\frac{\mathrm{4}}{\mathrm{5}}\right)^{\mathrm{3}} +.. \\ $$$$=\left(\mathrm{1}−\frac{\mathrm{4}}{\mathrm{5}}\right)^{\frac{−\mathrm{1}}{\mathrm{2}}} \\ $$$$=\left(\frac{\mathrm{1}}{\mathrm{5}}\right)^{\frac{−\mathrm{1}}{\mathrm{2}}} =\left(\mathrm{5}^{−\mathrm{1}} \right)^{\frac{−\mathrm{1}}{\mathrm{2}}} =\left(\mathrm{5}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} =\sqrt{\mathrm{5}} \\ $$$$\boldsymbol{{R}}{HS} \\ $$$$\mathrm{2}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{10}}+\frac{\mathrm{1}.\mathrm{3}}{\mathrm{10}.\mathrm{20}}+\frac{\mathrm{1}.\mathrm{3}.\mathrm{5}}{\mathrm{10}.\mathrm{20}.\mathrm{30}}+…\right) \\ $$$$=\mathrm{2}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{1}}{\mathrm{5}\:}+\frac{\mathrm{1}×\mathrm{3}}{\mathrm{2}×\mathrm{4}}×\frac{\mathrm{1}}{\mathrm{5}×\mathrm{5}}+\frac{\mathrm{1}×\mathrm{3}×\mathrm{5}}{\mathrm{2}×\mathrm{4}×\mathrm{6}}×\frac{\mathrm{1}}{\mathrm{5}×\mathrm{5}×\mathrm{5}}+..\right) \\ $$$$=\mathrm{2}\left[\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{5}}\right)+\frac{\mathrm{1}×\mathrm{3}}{\mathrm{2}×\mathrm{4}}\left(\frac{\mathrm{1}}{\mathrm{5}}\right)^{\mathrm{2}} +\frac{\mathrm{1}×\mathrm{3}×\mathrm{5}}{\mathrm{2}×\mathrm{4}×\mathrm{6}}\left(\frac{\mathrm{1}}{\mathrm{5}}\right)^{\mathrm{3}} +…\right] \\ $$$$=\mathrm{2}\left[\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{5}}\right)^{\frac{−\mathrm{1}}{\mathrm{2}}} \right] \\ $$$$=\mathrm{2}\left[\left(\frac{\mathrm{4}}{\mathrm{5}}\right)\right]^{\frac{−\mathrm{1}}{\mathrm{2}}} \\ $$$$=\mathrm{2}×\left(\mathrm{4}\right)^{\frac{−\mathrm{1}}{\mathrm{2}}} ×\left(\frac{\mathrm{1}}{\mathrm{5}}\right)^{\frac{−\mathrm{1}}{\mathrm{2}}} \\ $$$$=\mathrm{2}×\mathrm{2}^{−\mathrm{1}} ×\left(\mathrm{5}^{−\mathrm{1}} \right)^{\frac{−\mathrm{1}}{\mathrm{2}}} \\ $$$$=\mathrm{2}×\frac{\mathrm{1}}{\mathrm{2}}×\left(\mathrm{5}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$=\left(\mathrm{5}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} =\sqrt{\mathrm{5}}\: \\ $$$$\boldsymbol{{hence}}\:\boldsymbol{{proved}}… \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by Tawa1 last updated on 03/Mar/19

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
