Question Number 55663 by peter frank last updated on 01/Mar/19

Answered by tanmay.chaudhury50@gmail.com last updated on 01/Mar/19

$${b}_{\mathrm{1}} \:{b}_{\mathrm{2}\:} \:{b}_{\mathrm{3}} \:{b}_{\mathrm{4}} \:{b}_{\mathrm{5}} \:{b}_{\mathrm{6}} \:{b}_{\mathrm{7}} \:{b}_{\bigstar} \:\rightarrow{b}_{\bigstar} \rightarrow{particular}\:{boy} \\ $$$${group}\:\mathrm{7}={b}_{\bigstar} +\mathrm{2}{boy}+\mathrm{4}{girl} \\ $$$${group}\mathrm{7}={b}_{\bigstar} +\mathrm{3}{b}+\mathrm{3}{g} \\ $$$${g}\mathrm{7}={b}_{\bigstar} +\mathrm{4}{b}+\mathrm{2}{g} \\ $$$${g}\mathrm{7}={b}_{\bigstar} +\mathrm{5}{b}+\mathrm{1}{g} \\ $$$${g}\mathrm{7}={b}_{\bigstar} +\mathrm{6}{b} \\ $$$${probablity}= \\ $$$$\frac{\mathrm{1}{c}_{\mathrm{1}} ×\mathrm{7}{c}_{\mathrm{2}} ×\mathrm{4}{c}_{\mathrm{4}} +\mathrm{1}{c}_{\mathrm{1}} ×\mathrm{7}{c}_{\mathrm{3}} ×\mathrm{4}{c}_{\mathrm{3}} +\mathrm{1}{c}_{\mathrm{1}} ×\mathrm{7}{c}_{\mathrm{4}} ×\mathrm{4}{c}_{\mathrm{2}} +\mathrm{1}{c}_{\mathrm{1}} ×\mathrm{7}{c}_{\mathrm{5}} ×\mathrm{4}{c}_{\mathrm{1}} +\mathrm{1}{c}_{\mathrm{1}} ×\mathrm{7}{c}_{\mathrm{6}} }{\mathrm{12}{c}_{\mathrm{7}} } \\ $$$$=\frac{\mathrm{21}+\mathrm{35}×\mathrm{4}+\mathrm{35}×\mathrm{6}+\mathrm{21}×\mathrm{4}+\mathrm{1}×\mathrm{7}}{\frac{\mathrm{12}×\mathrm{11}×\mathrm{10}×\mathrm{9}×\mathrm{8}}{\mathrm{5}×\mathrm{4}×\mathrm{3}×\mathrm{2}}} \\ $$$$=\frac{\mathrm{21}+\mathrm{140}+\mathrm{210}+\mathrm{84}+\mathrm{7}}{\mathrm{11}×\mathrm{9}×\mathrm{8}} \\ $$$$=\frac{\mathrm{462}}{\mathrm{11}×\mathrm{9}×\mathrm{8}}=\frac{\mathrm{42}}{\mathrm{9}×\mathrm{8}} \\ $$$$=\frac{\mathrm{14}}{\mathrm{3}×\mathrm{8}} \\ $$$$=\frac{\mathrm{7}}{\mathrm{12}} \\ $$$${pls}\:{check}\:{calculation}… \\ $$
Commented by peter frank last updated on 02/Mar/19

$${thank}\:{you} \\ $$
Answered by mr W last updated on 02/Mar/19

$${to}\:{choose}\:\mathrm{7}\:{members}\:{from}\:\mathrm{12}\:{persons} \\ $$$${there}\:{are}\:{totally}\:{C}_{\mathrm{7}} ^{\mathrm{12}} \:{possibilities}. \\ $$$${if}\:{a}\:{special}\:{persion}\:{should}\:{be}\:{in}\:{the} \\ $$$${group},\:{we}\:{only}\:{need}\:{to}\:{choose}\:{the} \\ $$$${other}\:\mathrm{6}\:{members}\:{from}\:{the}\:{remaining} \\ $$$$\mathrm{11}\:{persons},\:{there}\:{are}\:{C}_{\mathrm{6}} ^{\mathrm{11}} \:{possibilities}. \\ $$$$\Rightarrow{p}=\frac{{C}_{\mathrm{6}} ^{\mathrm{11}} }{{C}_{\mathrm{7}} ^{\mathrm{12}} }=\frac{\mathrm{11}!×\mathrm{7}!×\mathrm{5}!}{\mathrm{6}!×\mathrm{5}!×\mathrm{12}!}=\frac{\mathrm{7}}{\mathrm{12}} \\ $$
Commented by peter frank last updated on 02/Mar/19

$${thank}\:{you} \\ $$
Commented by malwaan last updated on 03/Mar/19
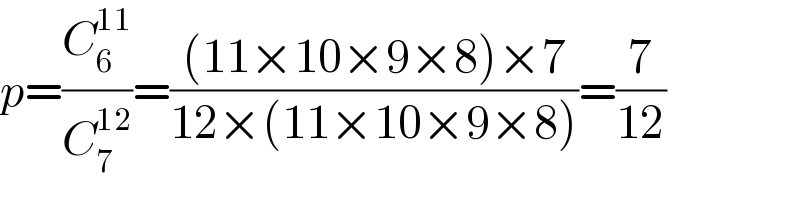
$${p}=\frac{{C}_{\mathrm{6}} ^{\mathrm{11}} }{{C}_{\mathrm{7}} ^{\mathrm{12}} }=\frac{\left(\mathrm{11}×\mathrm{10}×\mathrm{9}×\mathrm{8}\right)×\mathrm{7}}{\mathrm{12}×\left(\mathrm{11}×\mathrm{10}×\mathrm{9}×\mathrm{8}\right)}=\frac{\mathrm{7}}{\mathrm{12}} \\ $$
