Question Number 55948 by Tawa1 last updated on 06/Mar/19
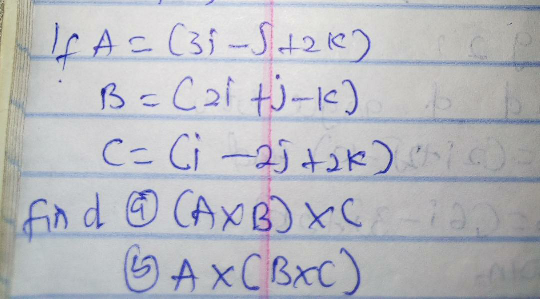
Answered by kaivan.ahmadi last updated on 07/Mar/19
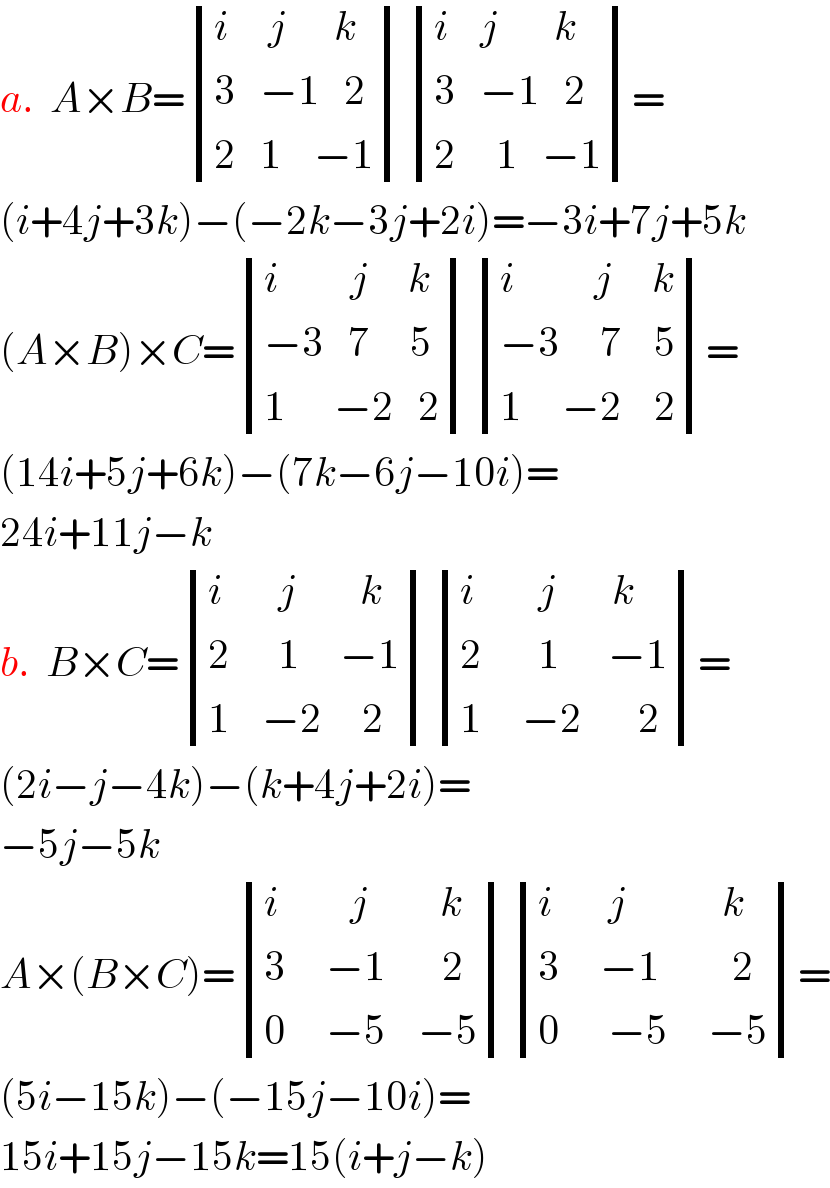
$${a}.\:\:{A}×{B}=\begin{vmatrix}{{i}\:\:\:\:\:{j}\:\:\:\:\:\:{k}}\\{\mathrm{3}\:\:\:−\mathrm{1}\:\:\:\mathrm{2}}\\{\mathrm{2}\:\:\:\mathrm{1}\:\:\:\:−\mathrm{1}}\end{vmatrix}\begin{vmatrix}{{i}\:\:\:\:{j}\:\:\:\:\:\:\:{k}}\\{\mathrm{3}\:\:\:−\mathrm{1}\:\:\:\mathrm{2}}\\{\mathrm{2}\:\:\:\:\:\mathrm{1}\:\:\:−\mathrm{1}}\end{vmatrix}= \\ $$$$\left({i}+\mathrm{4}{j}+\mathrm{3}{k}\right)−\left(−\mathrm{2}{k}−\mathrm{3}{j}+\mathrm{2}{i}\right)=−\mathrm{3}{i}+\mathrm{7}{j}+\mathrm{5}{k} \\ $$$$\left({A}×{B}\right)×{C}=\begin{vmatrix}{{i}\:\:\:\:\:\:\:\:\:{j}\:\:\:\:\:{k}}\\{−\mathrm{3}\:\:\:\mathrm{7}\:\:\:\:\:\mathrm{5}}\\{\mathrm{1}\:\:\:\:\:\:−\mathrm{2}\:\:\:\mathrm{2}}\end{vmatrix}\begin{vmatrix}{{i}\:\:\:\:\:\:\:\:\:\:{j}\:\:\:\:\:{k}}\\{−\mathrm{3}\:\:\:\:\:\mathrm{7}\:\:\:\:\mathrm{5}}\\{\mathrm{1}\:\:\:\:\:−\mathrm{2}\:\:\:\:\mathrm{2}}\end{vmatrix}= \\ $$$$\left(\mathrm{14}{i}+\mathrm{5}{j}+\mathrm{6}{k}\right)−\left(\mathrm{7}{k}−\mathrm{6}{j}−\mathrm{10}{i}\right)= \\ $$$$\mathrm{24}{i}+\mathrm{11}{j}−{k} \\ $$$${b}.\:\:{B}×{C}=\begin{vmatrix}{{i}\:\:\:\:\:\:\:{j}\:\:\:\:\:\:\:\:{k}}\\{\mathrm{2}\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:−\mathrm{1}}\\{\mathrm{1}\:\:\:\:−\mathrm{2}\:\:\:\:\:\mathrm{2}}\end{vmatrix}\begin{vmatrix}{{i}\:\:\:\:\:\:\:\:{j}\:\:\:\:\:\:\:{k}}\\{\mathrm{2}\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:−\mathrm{1}}\\{\mathrm{1}\:\:\:\:\:−\mathrm{2}\:\:\:\:\:\:\:\mathrm{2}}\end{vmatrix}= \\ $$$$\left(\mathrm{2}{i}−{j}−\mathrm{4}{k}\right)−\left({k}+\mathrm{4}{j}+\mathrm{2}{i}\right)= \\ $$$$−\mathrm{5}{j}−\mathrm{5}{k} \\ $$$${A}×\left({B}×{C}\right)=\begin{vmatrix}{{i}\:\:\:\:\:\:\:\:\:{j}\:\:\:\:\:\:\:\:\:{k}}\\{\mathrm{3}\:\:\:\:\:−\mathrm{1}\:\:\:\:\:\:\:\mathrm{2}}\\{\mathrm{0}\:\:\:\:\:−\mathrm{5}\:\:\:\:−\mathrm{5}}\end{vmatrix}\begin{vmatrix}{{i}\:\:\:\:\:\:\:{j}\:\:\:\:\:\:\:\:\:\:\:\:{k}}\\{\mathrm{3}\:\:\:\:\:−\mathrm{1}\:\:\:\:\:\:\:\:\:\mathrm{2}}\\{\mathrm{0}\:\:\:\:\:\:−\mathrm{5}\:\:\:\:\:−\mathrm{5}}\end{vmatrix}= \\ $$$$\left(\mathrm{5}{i}−\mathrm{15}{k}\right)−\left(−\mathrm{15}{j}−\mathrm{10}{i}\right)= \\ $$$$\mathrm{15}{i}+\mathrm{15}{j}−\mathrm{15}{k}=\mathrm{15}\left({i}+{j}−{k}\right) \\ $$
Commented by Tawa1 last updated on 07/Mar/19

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
