Question Number 55971 by bshahid010@gmail.com last updated on 07/Mar/19

Commented by tanmay.chaudhury50@gmail.com last updated on 07/Mar/19
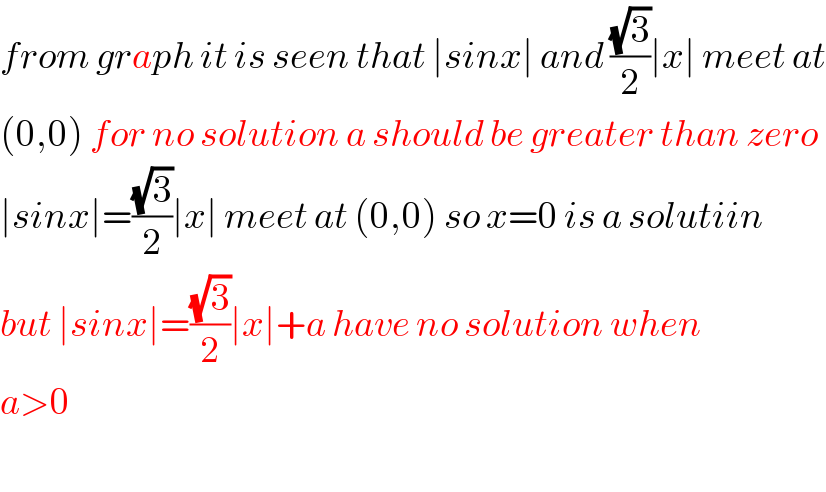
$${from}\:{graph}\:{it}\:{is}\:{seen}\:{that}\:\mid{sinx}\mid\:{and}\:\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mid{x}\mid\:{meet}\:{at} \\ $$$$\left(\mathrm{0},\mathrm{0}\right)\:{for}\:{no}\:{solution}\:{a}\:{should}\:{be}\:{greater}\:{than}\:{zero} \\ $$$$\mid{sinx}\mid=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mid{x}\mid\:{meet}\:{at}\:\left(\mathrm{0},\mathrm{0}\right)\:{so}\:{x}=\mathrm{0}\:{is}\:{a}\:{solutiin} \\ $$$${but}\:\mid{sinx}\mid=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mid{x}\mid+{a}\:{have}\:{no}\:{solution}\:{when} \\ $$$${a}>\mathrm{0} \\ $$$$ \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 07/Mar/19

Answered by mr W last updated on 07/Mar/19

Commented by mr W last updated on 07/Mar/19
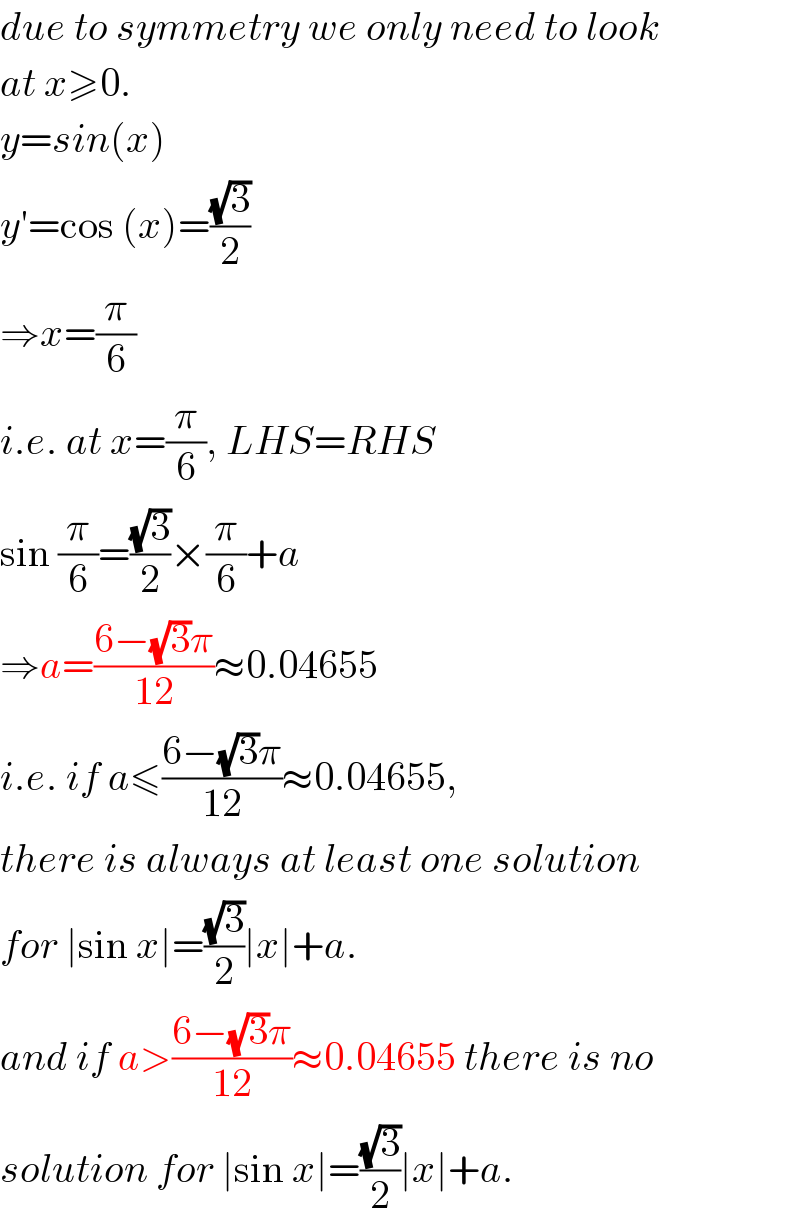
$${due}\:{to}\:{symmetry}\:{we}\:{only}\:{need}\:{to}\:{look} \\ $$$${at}\:{x}\geqslant\mathrm{0}. \\ $$$${y}={sin}\left({x}\right) \\ $$$${y}'=\mathrm{cos}\:\left({x}\right)=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$$\Rightarrow{x}=\frac{\pi}{\mathrm{6}} \\ $$$${i}.{e}.\:{at}\:{x}=\frac{\pi}{\mathrm{6}},\:{LHS}={RHS} \\ $$$$\mathrm{sin}\:\frac{\pi}{\mathrm{6}}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}×\frac{\pi}{\mathrm{6}}+{a} \\ $$$$\Rightarrow{a}=\frac{\mathrm{6}−\sqrt{\mathrm{3}}\pi}{\mathrm{12}}\approx\mathrm{0}.\mathrm{04655} \\ $$$${i}.{e}.\:{if}\:{a}\leqslant\frac{\mathrm{6}−\sqrt{\mathrm{3}}\pi}{\mathrm{12}}\approx\mathrm{0}.\mathrm{04655}, \\ $$$${there}\:{is}\:{always}\:{at}\:{least}\:{one}\:{solution} \\ $$$${for}\:\mid\mathrm{sin}\:{x}\mid=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mid{x}\mid+{a}. \\ $$$${and}\:{if}\:{a}>\frac{\mathrm{6}−\sqrt{\mathrm{3}}\pi}{\mathrm{12}}\approx\mathrm{0}.\mathrm{04655}\:{there}\:{is}\:{no} \\ $$$${solution}\:{for}\:\mid\mathrm{sin}\:{x}\mid=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mid{x}\mid+{a}. \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 07/Mar/19
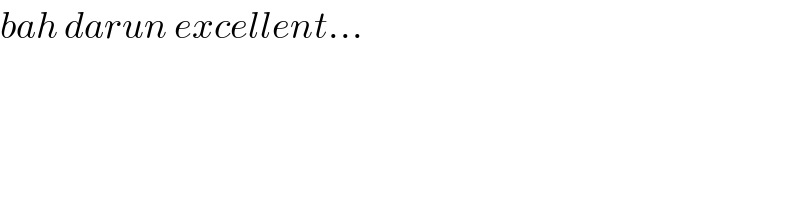
$${bah}\:{darun}\:{excellent}… \\ $$
Commented by mr W last updated on 07/Mar/19
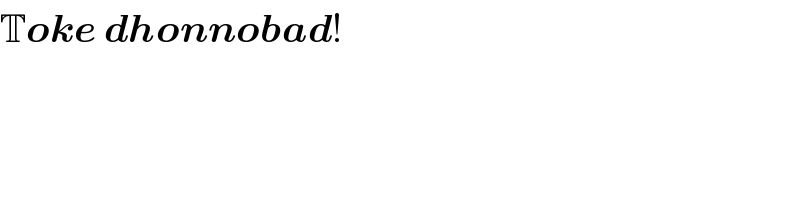
$$\mathbb{T}\boldsymbol{{oke}}\:\boldsymbol{{dhonnobad}}! \\ $$
Commented by mr W last updated on 07/Mar/19
$${hope}\:{it}'{s}\:{correctly}\:{written}. \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 07/Mar/19
$${nam}\:{ki}…{nischoi}\:{bangali}…{ami}\:{barrackpore}\:{ar}…{service} \\ $$$${in}\:{railway}…{nagpure}\:{thaki}… \\ $$
Commented by bshahid010@gmail.com last updated on 07/Mar/19

$$\mathrm{thank}\:\mathrm{u} \\ $$
