Question Number 55991 by bshahid010@gmail.com last updated on 07/Mar/19
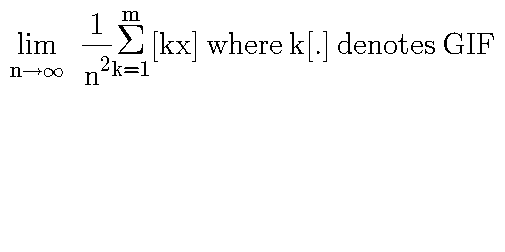
Commented by maxmathsup by imad last updated on 07/Mar/19
![let S_n (x)=(1/n^2 ) Σ_(k=1) ^m [kx]we have [kx]≤kx<[kx]+1 ⇒ kx−1<[kx]≤kx ⇒ (1/n^2 )Σ_(k=1) ^m (kx−1)<(1/n^2 )Σ_(k=1) ^m [kx)≤(1/n^2 )Σ_(k=1) ^m kx but (1/n^2 )Σ_(k=1) ^m (kx−1) =x ((Σ_(k=1) ^m k)/n^2 ) −(m/n^2 ) =x ((m(m+1))/(2n^2 )) −(m/n^2 ) =A_n also (1/n^2 )Σ_(k=1) ^m kx =x ((m(m+1))/n) =B_m if m is fixed lim_(n→+∞) A_n =0 and lim_(n→+∞) B_n =0 ⇒lim S_n (x)=0 if m is function of n its aother subject let suppose m ∼n ⇒ lim_(n→+∞) A_n =(x/2) =lim_(n→+∞) B_n ⇒lim_(n→+∞) S_n (x)=(x/2) .](https://www.tinkutara.com/question/Q56003.png)
$${let}\:\:{S}_{{n}} \left({x}\right)=\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\:\sum_{{k}=\mathrm{1}} ^{{m}} \:\left[{kx}\right]{we}\:{have}\:\:\:\left[{kx}\right]\leqslant{kx}<\left[{kx}\right]+\mathrm{1}\:\Rightarrow\:\:{kx}−\mathrm{1}<\left[{kx}\right]\leqslant{kx}\:\Rightarrow \\ $$$$\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\sum_{{k}=\mathrm{1}} ^{{m}} \:\left({kx}−\mathrm{1}\right)<\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\sum_{{k}=\mathrm{1}} ^{{m}} \left[{kx}\right)\leqslant\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\sum_{{k}=\mathrm{1}} ^{{m}} {kx}\:\:{but} \\ $$$$\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\sum_{{k}=\mathrm{1}} ^{{m}} \left({kx}−\mathrm{1}\right)\:={x}\:\frac{\sum_{{k}=\mathrm{1}} ^{{m}} {k}}{{n}^{\mathrm{2}} }\:−\frac{{m}}{{n}^{\mathrm{2}} }\:={x}\:\frac{{m}\left({m}+\mathrm{1}\right)}{\mathrm{2}{n}^{\mathrm{2}} }\:−\frac{{m}}{{n}^{\mathrm{2}} }\:={A}_{{n}} \:\:{also} \\ $$$$\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\sum_{{k}=\mathrm{1}} ^{{m}} {kx}\:={x}\:\frac{{m}\left({m}+\mathrm{1}\right)}{{n}}\:={B}_{{m}} \\ $$$${if}\:{m}\:{is}\:{fixed}\:\:\:{lim}_{{n}\rightarrow+\infty} \:{A}_{{n}} =\mathrm{0}\:{and}\:{lim}_{{n}\rightarrow+\infty} \:{B}_{{n}} =\mathrm{0}\:\Rightarrow{lim}\:{S}_{{n}} \left({x}\right)=\mathrm{0} \\ $$$${if}\:\:{m}\:{is}\:{function}\:{of}\:\:{n}\:\:{its}\:{aother}\:{subject}\:{let}\:{suppose}\:{m}\:\sim{n}\:\Rightarrow \\ $$$${lim}_{{n}\rightarrow+\infty} {A}_{{n}} =\frac{{x}}{\mathrm{2}}\:={lim}_{{n}\rightarrow+\infty} \:\:\:\:{B}_{{n}} \:\Rightarrow{lim}_{{n}\rightarrow+\infty} \:{S}_{{n}} \left({x}\right)=\frac{{x}}{\mathrm{2}}\:. \\ $$$$ \\ $$
Commented by maxmathsup by imad last updated on 07/Mar/19
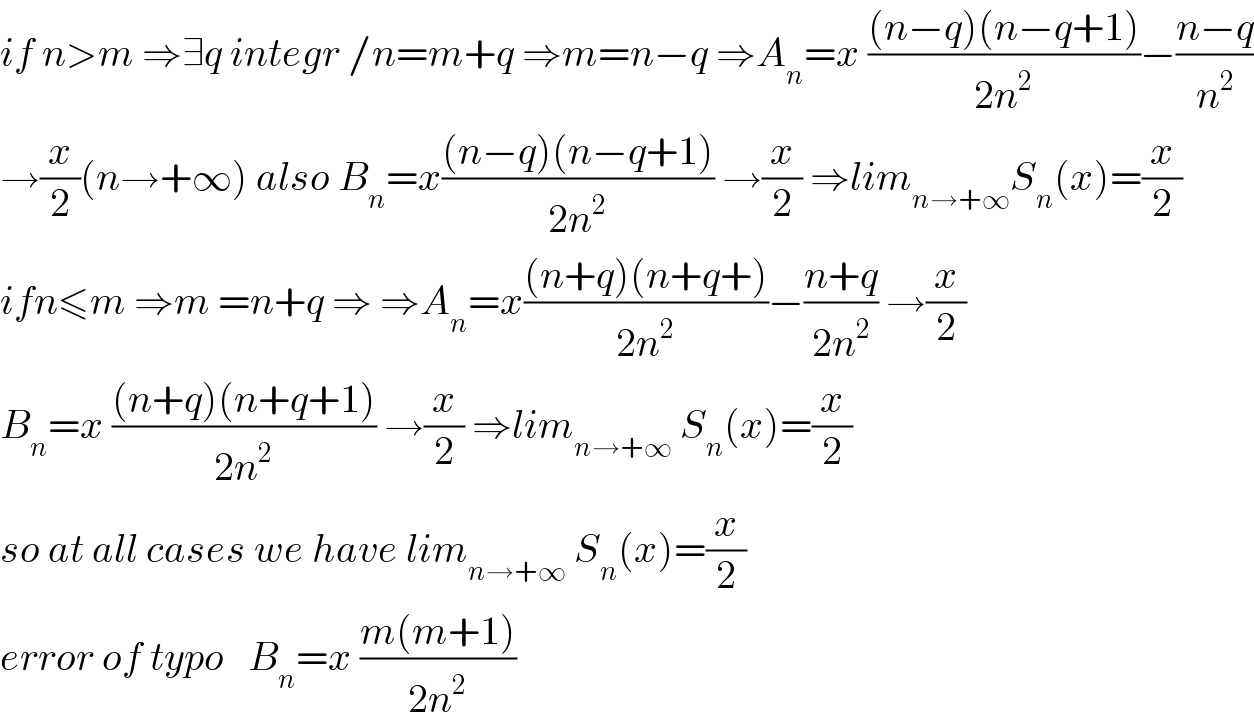
$${if}\:{n}>{m}\:\Rightarrow\exists{q}\:{integr}\:/{n}={m}+{q}\:\Rightarrow{m}={n}−{q}\:\Rightarrow{A}_{{n}} ={x}\:\frac{\left({n}−{q}\right)\left({n}−{q}+\mathrm{1}\right)}{\mathrm{2}{n}^{\mathrm{2}} }−\frac{{n}−{q}}{{n}^{\mathrm{2}} } \\ $$$$\rightarrow\frac{{x}}{\mathrm{2}}\left({n}\rightarrow+\infty\right)\:{also}\:{B}_{{n}} ={x}\frac{\left({n}−{q}\right)\left({n}−{q}+\mathrm{1}\right)}{\mathrm{2}{n}^{\mathrm{2}} }\:\rightarrow\frac{{x}}{\mathrm{2}}\:\Rightarrow{lim}_{{n}\rightarrow+\infty} {S}_{{n}} \left({x}\right)=\frac{{x}}{\mathrm{2}} \\ $$$${ifn}\leqslant{m}\:\Rightarrow{m}\:={n}+{q}\:\Rightarrow\:\Rightarrow{A}_{{n}} ={x}\frac{\left({n}+{q}\right)\left({n}+{q}+\right)}{\mathrm{2}{n}^{\mathrm{2}} }−\frac{{n}+{q}}{\mathrm{2}{n}^{\mathrm{2}} }\:\rightarrow\frac{{x}}{\mathrm{2}} \\ $$$${B}_{{n}} ={x}\:\frac{\left({n}+{q}\right)\left({n}+{q}+\mathrm{1}\right)}{\mathrm{2}{n}^{\mathrm{2}} }\:\rightarrow\frac{{x}}{\mathrm{2}}\:\Rightarrow{lim}_{{n}\rightarrow+\infty} \:{S}_{{n}} \left({x}\right)=\frac{{x}}{\mathrm{2}} \\ $$$${so}\:{at}\:{all}\:{cases}\:{we}\:{have}\:{lim}_{{n}\rightarrow+\infty} \:{S}_{{n}} \left({x}\right)=\frac{{x}}{\mathrm{2}} \\ $$$${error}\:{of}\:{typo}\:\:\:{B}_{{n}} ={x}\:\frac{{m}\left({m}+\mathrm{1}\right)}{\mathrm{2}{n}^{\mathrm{2}} } \\ $$
