Question Number 56042 by Tawa1 last updated on 09/Mar/19

Answered by math1967 last updated on 09/Mar/19
![c_r ^n =((n!)/(r!(n−r)!))×(((n−r+1))/((n−r+1)))=((n!×(n−r+1))/(r×(r−1)!(n−r+1)!)) =((n!)/((r−1)!(n−r+1)!))×[((n−r+1)/r)] = ^n c_(r−1) [(((n−r+1))/r)]](https://www.tinkutara.com/question/Q56043.png)
$$\overset{{n}} {{c}}_{{r}} =\frac{{n}!}{{r}!\left({n}−{r}\right)!}×\frac{\left({n}−{r}+\mathrm{1}\right)}{\left({n}−{r}+\mathrm{1}\right)}=\frac{{n}!×\left({n}−{r}+\mathrm{1}\right)}{{r}×\left({r}−\mathrm{1}\right)!\left({n}−{r}+\mathrm{1}\right)!}\: \\ $$$$=\frac{{n}!}{\left({r}−\mathrm{1}\right)!\left({n}−{r}+\mathrm{1}\right)!}×\left[\frac{{n}−{r}+\mathrm{1}}{{r}}\right] \\ $$$$=\overset{{n}} {\:}{c}_{{r}−\mathrm{1}} \left[\frac{\left({n}−{r}+\mathrm{1}\right)}{{r}}\right] \\ $$
Commented by Tawa1 last updated on 09/Mar/19

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Answered by math1967 last updated on 09/Mar/19
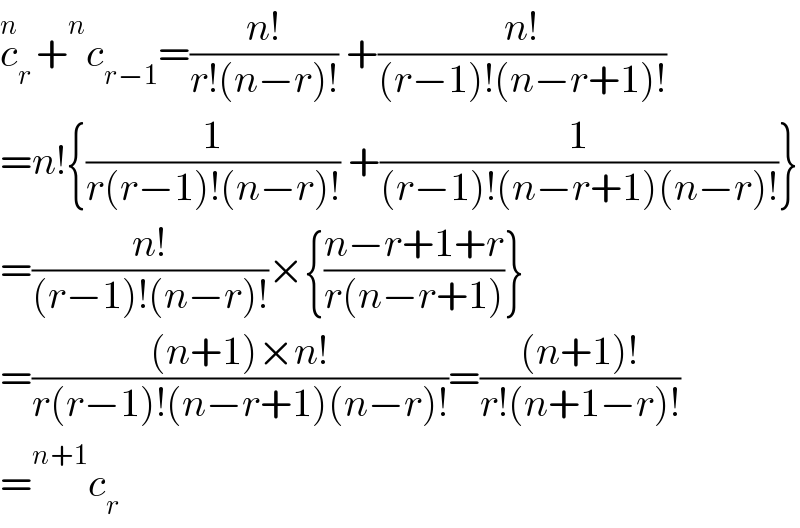
$$\overset{{n}} {{c}}_{{r}\:} +\overset{{n}} {\:}{c}_{{r}−\mathrm{1}} =\frac{{n}!}{{r}!\left({n}−{r}\right)!}\:+\frac{{n}!}{\left({r}−\mathrm{1}\right)!\left({n}−{r}+\mathrm{1}\right)!} \\ $$$$={n}!\left\{\frac{\mathrm{1}}{{r}\left({r}−\mathrm{1}\right)!\left({n}−{r}\right)!}\:+\frac{\mathrm{1}}{\left({r}−\mathrm{1}\right)!\left({n}−{r}+\mathrm{1}\right)\left({n}−{r}\right)!}\right\} \\ $$$$=\frac{{n}!}{\left({r}−\mathrm{1}\right)!\left({n}−{r}\right)!}×\left\{\frac{{n}−{r}+\mathrm{1}+{r}}{{r}\left({n}−{r}+\mathrm{1}\right)}\right\} \\ $$$$=\frac{\left({n}+\mathrm{1}\right)×{n}!}{{r}\left({r}−\mathrm{1}\right)!\left({n}−{r}+\mathrm{1}\right)\left({n}−{r}\right)!}=\frac{\left({n}+\mathrm{1}\right)!}{{r}!\left({n}+\mathrm{1}−{r}\right)!} \\ $$$$=\overset{{n}+\mathrm{1}} {\:}{c}_{{r}} \\ $$
Commented by Tawa1 last updated on 09/Mar/19

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Commented by math1967 last updated on 09/Mar/19

$${GOD}\:{IS}\:\:{A}\:{CIRCLE}\:{WHOSE}\:{CENTRE} \\ $$$${IS}\:{EVERYWHERE},{BUT}\:\:{WHOSE} \\ $$$${CIRCUMFERENCE}\:{IS}\:{NO}\:{WHERE} \\ $$
