Menu Close

Question-56051

Tinku Tara 0 Comments
Pin




Question Number 56051 by naka3546 last updated on 09/Mar/19
Answered by mr W last updated on 09/Mar/19
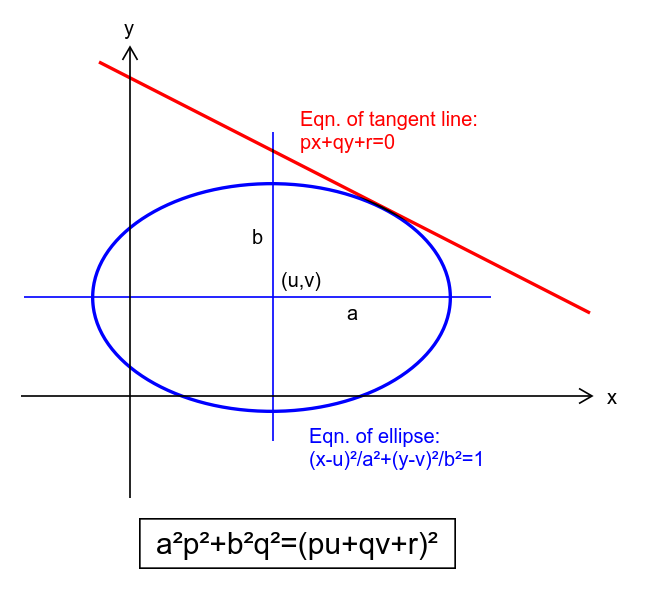
Commented by mr W last updated on 10/Mar/19
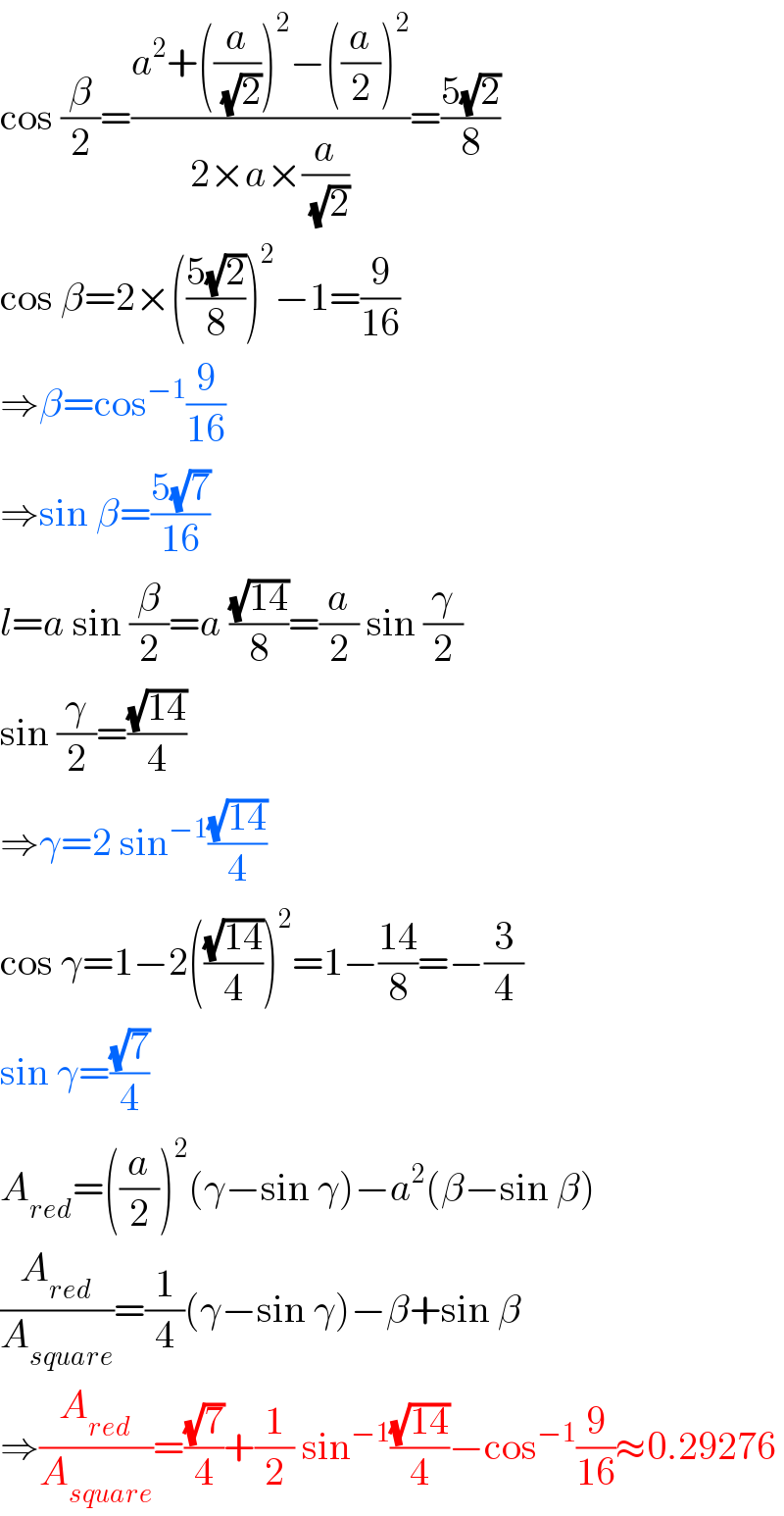
cos (β/2)=((a^2 +((a/( (√2))))^2 −((a/2))^2 )/(2×a×(a/( (√2)))))=((5(√2))/8) cos β=2×(((5(√2))/8))^2 −1=(9/(16)) ⇒β=cos^(−1) (9/(16)) ⇒sin β=((5(√7))/(16)) l=a sin (β/2)=a ((√(14))/8)=(a/2) sin (γ/2) sin (γ/2)=((√(14))/4) ⇒γ=2 sin^(−1) ((√(14))/4) cos γ=1−2(((√(14))/4))^2 =1−((14)/8)=−(3/4) sin γ=((√7)/4) A_(red) =((a/2))^2 (γ−sin γ)−a^2 (β−sin β) (A_(red) /A_(square) )=(1/4)(γ−sin γ)−β+sin β ⇒(A_(red) /A_(square) )=((√7)/4)+(1/2) sin^(−1) ((√(14))/4)−cos^(−1) (9/(16))≈0.29276
$$\mathrm{cos}\:\frac{\beta}{\mathrm{2}}=\frac{{a}^{\mathrm{2}} +\left(\frac{{a}}{\:\sqrt{\mathrm{2}}}\right)^{\mathrm{2}} −\left(\frac{{a}}{\mathrm{2}}\right)^{\mathrm{2}} }{\mathrm{2}×{a}×\frac{{a}}{\:\sqrt{\mathrm{2}}}}=\frac{\mathrm{5}\sqrt{\mathrm{2}}}{\mathrm{8}} \\ $$$$\mathrm{cos}\:\beta=\mathrm{2}×\left(\frac{\mathrm{5}\sqrt{\mathrm{2}}}{\mathrm{8}}\right)^{\mathrm{2}} −\mathrm{1}=\frac{\mathrm{9}}{\mathrm{16}} \\ $$$$\Rightarrow\beta=\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{9}}{\mathrm{16}} \\ $$$$\Rightarrow\mathrm{sin}\:\beta=\frac{\mathrm{5}\sqrt{\mathrm{7}}}{\mathrm{16}} \\ $$$${l}={a}\:\mathrm{sin}\:\frac{\beta}{\mathrm{2}}={a}\:\frac{\sqrt{\mathrm{14}}}{\mathrm{8}}=\frac{{a}}{\mathrm{2}}\:\mathrm{sin}\:\frac{\gamma}{\mathrm{2}} \\ $$$$\mathrm{sin}\:\frac{\gamma}{\mathrm{2}}=\frac{\sqrt{\mathrm{14}}}{\mathrm{4}} \\ $$$$\Rightarrow\gamma=\mathrm{2}\:\mathrm{sin}^{−\mathrm{1}} \frac{\sqrt{\mathrm{14}}}{\mathrm{4}} \\ $$$$\mathrm{cos}\:\gamma=\mathrm{1}−\mathrm{2}\left(\frac{\sqrt{\mathrm{14}}}{\mathrm{4}}\right)^{\mathrm{2}} =\mathrm{1}−\frac{\mathrm{14}}{\mathrm{8}}=−\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$\mathrm{sin}\:\gamma=\frac{\sqrt{\mathrm{7}}}{\mathrm{4}} \\ $$$${A}_{{red}} =\left(\frac{{a}}{\mathrm{2}}\right)^{\mathrm{2}} \left(\gamma−\mathrm{sin}\:\gamma\right)−{a}^{\mathrm{2}} \left(\beta−\mathrm{sin}\:\beta\right) \\ $$$$\frac{{A}_{{red}} }{{A}_{{square}} }=\frac{\mathrm{1}}{\mathrm{4}}\left(\gamma−\mathrm{sin}\:\gamma\right)−\beta+\mathrm{sin}\:\beta \\ $$$$\Rightarrow\frac{{A}_{{red}} }{{A}_{{square}} }=\frac{\sqrt{\mathrm{7}}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{2}}\:\mathrm{sin}^{−\mathrm{1}} \frac{\sqrt{\mathrm{14}}}{\mathrm{4}}−\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{9}}{\mathrm{16}}\approx\mathrm{0}.\mathrm{29276} \\ $$
Answered by MJS last updated on 09/Mar/19
an easy one: turn by 45° side of square =1 big circle: x^2 +y^2 =1 small circle: x^2 +(y−((√2)/2))^2 =(1/4) intersection at x=±((√(14))/8) red area: 4∫_0 ^((√(14))/8) (((√2)/2)+((√(1−4x^2 ))/2)−(√(1−x^2 )))dx= =((√7)/4)+(1/2)arcsin ((√(14))/4) −2arcsin ((√(14))/8) ≈.292763
$$\mathrm{an}\:\mathrm{easy}\:\mathrm{one}: \\ $$$$\mathrm{turn}\:\mathrm{by}\:\mathrm{45}° \\ $$$$\mathrm{side}\:\mathrm{of}\:\mathrm{square}\:=\mathrm{1} \\ $$$$\mathrm{big}\:\mathrm{circle}:\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{1} \\ $$$$\mathrm{small}\:\mathrm{circle}:\:{x}^{\mathrm{2}} +\left({y}−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\right)^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\mathrm{intersection}\:\mathrm{at}\:{x}=\pm\frac{\sqrt{\mathrm{14}}}{\mathrm{8}} \\ $$$$\mathrm{red}\:\mathrm{area}:\:\mathrm{4}\underset{\mathrm{0}} {\overset{\frac{\sqrt{\mathrm{14}}}{\mathrm{8}}} {\int}}\left(\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}+\frac{\sqrt{\mathrm{1}−\mathrm{4}{x}^{\mathrm{2}} }}{\mathrm{2}}−\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\right){dx}= \\ $$$$=\frac{\sqrt{\mathrm{7}}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{arcsin}\:\frac{\sqrt{\mathrm{14}}}{\mathrm{4}}\:−\mathrm{2arcsin}\:\frac{\sqrt{\mathrm{14}}}{\mathrm{8}}\:\approx.\mathrm{292763} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *