Question Number 56120 by Tawa1 last updated on 10/Mar/19

Answered by 121194 last updated on 10/Mar/19
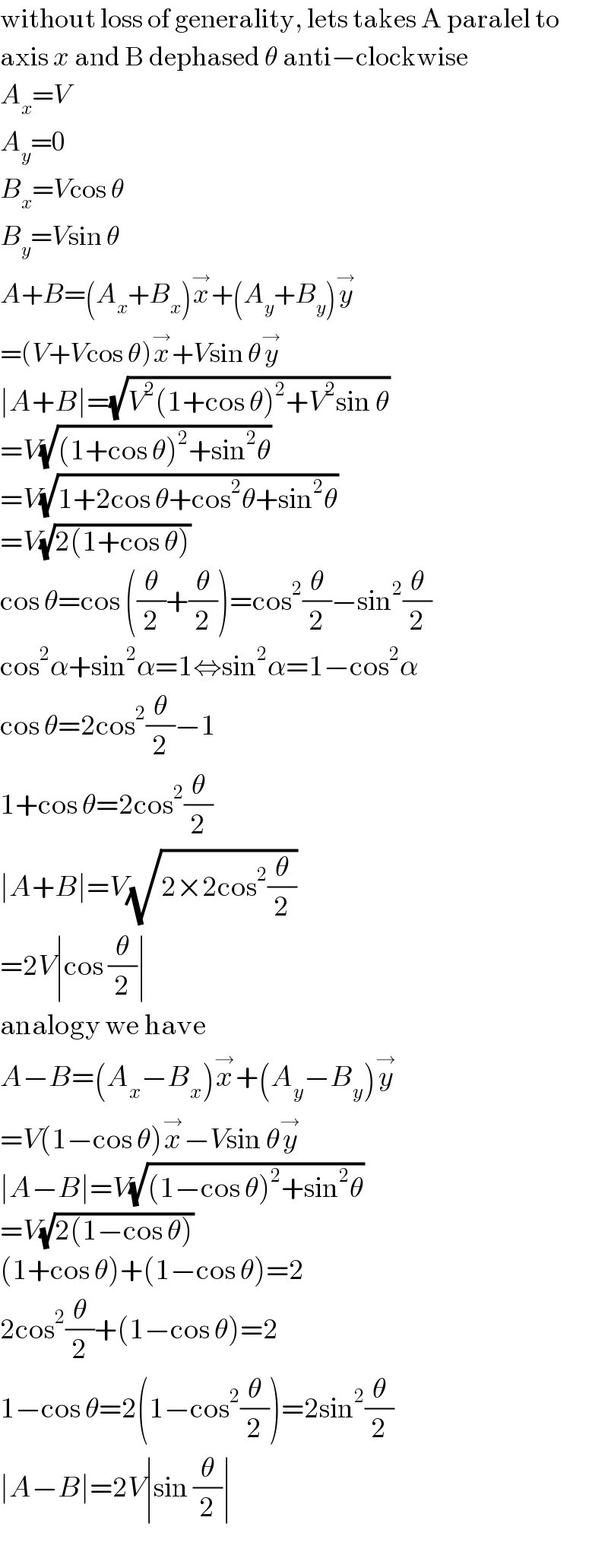
$$\mathrm{without}\:\mathrm{loss}\:\mathrm{of}\:\mathrm{generality},\:\mathrm{lets}\:\mathrm{takes}\:\mathrm{A}\:\mathrm{paralel}\:\mathrm{to} \\ $$$$\mathrm{axis}\:{x}\:\mathrm{and}\:\mathrm{B}\:\mathrm{dephased}\:\theta\:\mathrm{anti}−\mathrm{clockwise} \\ $$$${A}_{{x}} ={V} \\ $$$${A}_{{y}} =\mathrm{0} \\ $$$${B}_{{x}} ={V}\mathrm{cos}\:\theta \\ $$$${B}_{{y}} ={V}\mathrm{sin}\:\theta \\ $$$${A}+{B}=\left({A}_{{x}} +{B}_{{x}} \right)\overset{\rightarrow} {{x}}+\left({A}_{{y}} +{B}_{{y}} \right)\overset{\rightarrow} {{y}} \\ $$$$=\left({V}+{V}\mathrm{cos}\:\theta\right)\overset{\rightarrow} {{x}}+{V}\mathrm{sin}\:\theta\overset{\rightarrow} {{y}} \\ $$$$\mid{A}+{B}\mid=\sqrt{{V}^{\mathrm{2}} \left(\mathrm{1}+\mathrm{cos}\:\theta\right)^{\mathrm{2}} +{V}^{\mathrm{2}} \mathrm{sin}\:\theta} \\ $$$$={V}\sqrt{\left(\mathrm{1}+\mathrm{cos}\:\theta\right)^{\mathrm{2}} +\mathrm{sin}^{\mathrm{2}} \theta} \\ $$$$={V}\sqrt{\mathrm{1}+\mathrm{2cos}\:\theta+\mathrm{cos}^{\mathrm{2}} \theta+\mathrm{sin}^{\mathrm{2}} \theta} \\ $$$$={V}\sqrt{\mathrm{2}\left(\mathrm{1}+\mathrm{cos}\:\theta\right)} \\ $$$$\mathrm{cos}\:\theta=\mathrm{cos}\:\left(\frac{\theta}{\mathrm{2}}+\frac{\theta}{\mathrm{2}}\right)=\mathrm{cos}^{\mathrm{2}} \frac{\theta}{\mathrm{2}}−\mathrm{sin}^{\mathrm{2}} \frac{\theta}{\mathrm{2}} \\ $$$$\mathrm{cos}^{\mathrm{2}} \alpha+\mathrm{sin}^{\mathrm{2}} \alpha=\mathrm{1}\Leftrightarrow\mathrm{sin}^{\mathrm{2}} \alpha=\mathrm{1}−\mathrm{cos}^{\mathrm{2}} \alpha \\ $$$$\mathrm{cos}\:\theta=\mathrm{2cos}^{\mathrm{2}} \frac{\theta}{\mathrm{2}}−\mathrm{1} \\ $$$$\mathrm{1}+\mathrm{cos}\:\theta=\mathrm{2cos}^{\mathrm{2}} \frac{\theta}{\mathrm{2}} \\ $$$$\mid{A}+{B}\mid={V}\sqrt{\mathrm{2}×\mathrm{2cos}^{\mathrm{2}} \frac{\theta}{\mathrm{2}}} \\ $$$$=\mathrm{2}{V}\mid\mathrm{cos}\:\frac{\theta}{\mathrm{2}}\mid \\ $$$$\mathrm{analogy}\:\mathrm{we}\:\mathrm{have} \\ $$$${A}−{B}=\left({A}_{{x}} −{B}_{{x}} \right)\overset{\rightarrow} {{x}}+\left({A}_{{y}} −{B}_{{y}} \right)\overset{\rightarrow} {{y}} \\ $$$$={V}\left(\mathrm{1}−\mathrm{cos}\:\theta\right)\overset{\rightarrow} {{x}}−{V}\mathrm{sin}\:\theta\overset{\rightarrow} {{y}} \\ $$$$\mid{A}−{B}\mid={V}\sqrt{\left(\mathrm{1}−\mathrm{cos}\:\theta\right)^{\mathrm{2}} +\mathrm{sin}^{\mathrm{2}} \theta} \\ $$$$={V}\sqrt{\mathrm{2}\left(\mathrm{1}−\mathrm{cos}\:\theta\right)} \\ $$$$\left(\mathrm{1}+\mathrm{cos}\:\theta\right)+\left(\mathrm{1}−\mathrm{cos}\:\theta\right)=\mathrm{2} \\ $$$$\mathrm{2cos}^{\mathrm{2}} \frac{\theta}{\mathrm{2}}+\left(\mathrm{1}−\mathrm{cos}\:\theta\right)=\mathrm{2} \\ $$$$\mathrm{1}−\mathrm{cos}\:\theta=\mathrm{2}\left(\mathrm{1}−\mathrm{cos}^{\mathrm{2}} \frac{\theta}{\mathrm{2}}\right)=\mathrm{2sin}^{\mathrm{2}} \frac{\theta}{\mathrm{2}} \\ $$$$\mid{A}−{B}\mid=\mathrm{2}{V}\mid\mathrm{sin}\:\frac{\theta}{\mathrm{2}}\mid \\ $$
Commented by Tawa1 last updated on 10/Mar/19
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{appreciate}. \\ $$
