Question Number 56124 by Tawa1 last updated on 10/Mar/19
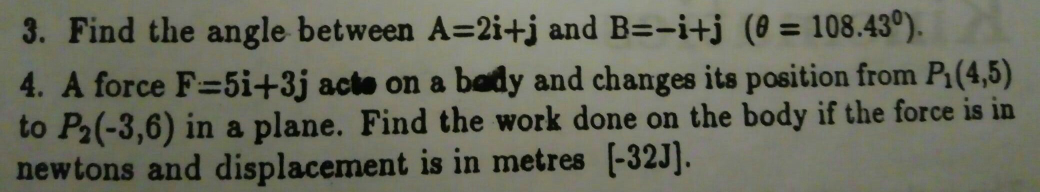
Answered by tanmay.chaudhury50@gmail.com last updated on 11/Mar/19
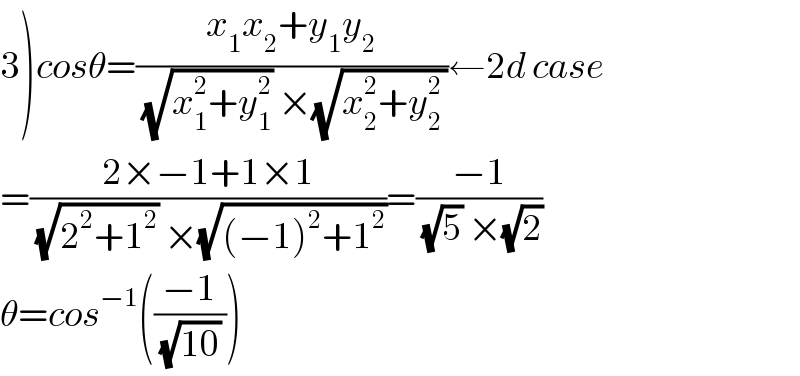
$$\left.\mathrm{3}\right){cos}\theta=\frac{{x}_{\mathrm{1}} {x}_{\mathrm{2}} +{y}_{\mathrm{1}} {y}_{\mathrm{2}} }{\:\sqrt{{x}_{\mathrm{1}} ^{\mathrm{2}} +{y}_{\mathrm{1}} ^{\mathrm{2}} }\:×\sqrt{{x}_{\mathrm{2}} ^{\mathrm{2}} +{y}_{\mathrm{2}\:} ^{\mathrm{2}} }}\leftarrow\mathrm{2}{d}\:{case} \\ $$$$=\frac{\mathrm{2}×−\mathrm{1}+\mathrm{1}×\mathrm{1}}{\:\sqrt{\mathrm{2}^{\mathrm{2}} +\mathrm{1}^{\mathrm{2}} }\:×\sqrt{\left(−\mathrm{1}\right)^{\mathrm{2}} +\mathrm{1}^{\mathrm{2}} }}=\frac{−\mathrm{1}}{\:\sqrt{\mathrm{5}}\:×\sqrt{\mathrm{2}}} \\ $$$$\theta={cos}^{−\mathrm{1}} \left(\frac{−\mathrm{1}}{\:\sqrt{\mathrm{10}}\:}\right) \\ $$
Commented by Tawa1 last updated on 11/Mar/19
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 11/Mar/19
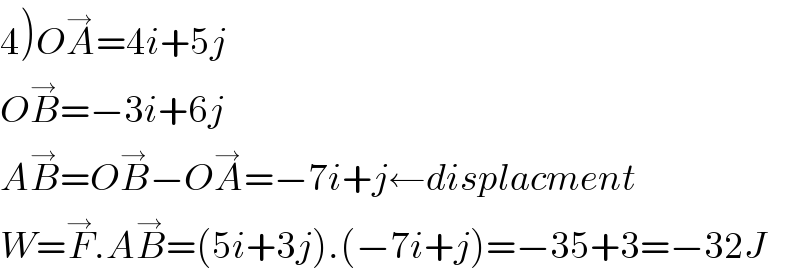
$$\left.\mathrm{4}\right){O}\overset{\rightarrow} {{A}}=\mathrm{4}{i}+\mathrm{5}{j} \\ $$$${O}\overset{\rightarrow} {{B}}=−\mathrm{3}{i}+\mathrm{6}{j} \\ $$$${A}\overset{\rightarrow} {{B}}={O}\overset{\rightarrow} {{B}}−{O}\overset{\rightarrow} {{A}}=−\mathrm{7}{i}+{j}\leftarrow{displacment} \\ $$$${W}=\overset{\rightarrow} {{F}}.{A}\overset{\rightarrow} {{B}}=\left(\mathrm{5}{i}+\mathrm{3}{j}\right).\left(−\mathrm{7}{i}+{j}\right)=−\mathrm{35}+\mathrm{3}=−\mathrm{32}{J} \\ $$
Commented by Tawa1 last updated on 11/Mar/19
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
