Question Number 56245 by Gulay last updated on 12/Mar/19
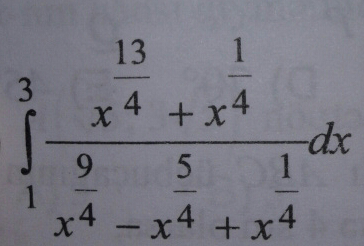
Commented by Gulay last updated on 12/Mar/19

$$\mathrm{sir}\:\mathrm{plz}\:\mathrm{help}\left[\mathrm{me}\right. \\ $$$$ \\ $$
Answered by math1967 last updated on 12/Mar/19
![∫_(1 ) ^3 ((x^(1/4) (x^3 +1)dx )/(x^(1/4) (x^2 −x+1)))=∫_1 ^3 (((x+1)(x^2 −x+1)dx)/((x^2 −x+1))) =∫_1 ^3 (x+1)dx=[(x^2 /2)+x]_1 ^3 =((9/2)+3)−((1/2)+1) =6 ans](https://www.tinkutara.com/question/Q56250.png)
$$\underset{\mathrm{1}\:} {\overset{\mathrm{3}} {\int}}\frac{{x}^{\frac{\mathrm{1}}{\mathrm{4}}} \left({x}^{\mathrm{3}} +\mathrm{1}\right){dx}\:\:}{{x}^{\frac{\mathrm{1}}{\mathrm{4}}} \left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)}=\underset{\mathrm{1}} {\overset{\mathrm{3}} {\int}}\frac{\left({x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right){dx}}{\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)} \\ $$$$=\underset{\mathrm{1}} {\overset{\mathrm{3}} {\int}}\left({x}+\mathrm{1}\right){dx}=\left[\frac{{x}^{\mathrm{2}} }{\mathrm{2}}+{x}\right]_{\mathrm{1}} ^{\mathrm{3}} =\left(\frac{\mathrm{9}}{\mathrm{2}}+\mathrm{3}\right)−\left(\frac{\mathrm{1}}{\mathrm{2}}+\mathrm{1}\right)\: \\ $$$$=\mathrm{6}\:{ans} \\ $$
Commented by Gulay last updated on 12/Mar/19

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$$$ \\ $$
Answered by Kunal12588 last updated on 13/Mar/19
![∫_1 ^3 ((x^((13)/4) +x^(1/4) )/(x^(9/4) −x^(5/4) +x^(1/4) ))dx=∫_1 ^3 ((x^((12+1)/4) +x^(1/4) )/(x^((8+1)/4) −x^((4+1)/4) +x^(1/4) ))dx =∫_1 ^3 ((x^3 ×x^(1/4) +x^(1/4) )/(x^2 ×x^(1/4) −x×x^(1/4) +x^(1/4) ))dx =∫_1 ^3 ((x^(1/4) (x^3 +1))/(x^(1/4) (x^2 −x+1)))dx=∫_1 ^3 (((x+1)(x^2 −x+1))/(x^2 −x+1))dx =∫_1 ^3 (x+1)dx=∫_1 ^3 x dx+∫_1 ^3 1 dx=(1/2)[x^2 ]_1 ^3 +[x]_1 ^3 =(1/2)(3^2 −1)+(3−1)=4+2=6 I am new in calculus.if there is any mistake pls tell me i will rectify](https://www.tinkutara.com/question/Q56254.png)
$$\underset{\mathrm{1}} {\overset{\mathrm{3}} {\int}}\:\frac{{x}^{\frac{\mathrm{13}}{\mathrm{4}}} +{x}^{\frac{\mathrm{1}}{\mathrm{4}}} }{{x}^{\frac{\mathrm{9}}{\mathrm{4}}} −{x}^{\frac{\mathrm{5}}{\mathrm{4}}} +{x}^{\frac{\mathrm{1}}{\mathrm{4}}} }{dx}=\underset{\mathrm{1}} {\overset{\mathrm{3}} {\int}}\frac{{x}^{\frac{\mathrm{12}+\mathrm{1}}{\mathrm{4}}} +{x}^{\frac{\mathrm{1}}{\mathrm{4}}} }{{x}^{\frac{\mathrm{8}+\mathrm{1}}{\mathrm{4}}} −{x}^{\frac{\mathrm{4}+\mathrm{1}}{\mathrm{4}}} +{x}^{\frac{\mathrm{1}}{\mathrm{4}}} }{dx} \\ $$$$=\underset{\mathrm{1}} {\overset{\mathrm{3}} {\int}}\frac{{x}^{\mathrm{3}} ×{x}^{\mathrm{1}/\mathrm{4}} +{x}^{\mathrm{1}/\mathrm{4}} }{{x}^{\mathrm{2}} ×{x}^{\mathrm{1}/\mathrm{4}} −{x}×{x}^{\mathrm{1}/\mathrm{4}} +{x}^{\mathrm{1}/\mathrm{4}} }{dx} \\ $$$$=\underset{\mathrm{1}} {\overset{\mathrm{3}} {\int}}\frac{{x}^{\mathrm{1}/\mathrm{4}} \left({x}^{\mathrm{3}} +\mathrm{1}\right)}{{x}^{\mathrm{1}/\mathrm{4}} \left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)}{dx}=\underset{\mathrm{1}} {\overset{\mathrm{3}} {\int}}\frac{\left({x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)}{{x}^{\mathrm{2}} −{x}+\mathrm{1}}{dx} \\ $$$$=\underset{\mathrm{1}} {\overset{\mathrm{3}} {\int}}\left({x}+\mathrm{1}\right){dx}=\underset{\mathrm{1}} {\overset{\mathrm{3}} {\int}}{x}\:{dx}+\underset{\mathrm{1}} {\overset{\mathrm{3}} {\int}}\mathrm{1}\:{dx}=\frac{\mathrm{1}}{\mathrm{2}}\left[{x}^{\mathrm{2}} \right]_{\mathrm{1}} ^{\mathrm{3}} +\left[{x}\right]_{\mathrm{1}} ^{\mathrm{3}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{3}^{\mathrm{2}} −\mathrm{1}\right)+\left(\mathrm{3}−\mathrm{1}\right)=\mathrm{4}+\mathrm{2}=\mathrm{6} \\ $$$${I}\:{am}\:{new}\:{in}\:{calculus}.{if}\:{there}\:{is}\:{any} \\ $$$${mistake}\:{pls}\:{tell}\:{me}\:\:{i}\:{will}\:{rectify} \\ $$
Commented by Prithwish sen last updated on 13/Mar/19
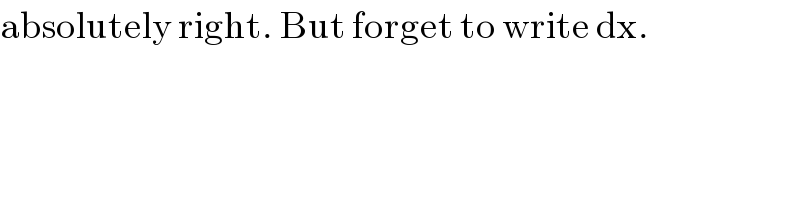
$$\mathrm{absolutely}\:\mathrm{right}.\:\mathrm{But}\:\mathrm{forget}\:\mathrm{to}\:\mathrm{write}\:\mathrm{dx}. \\ $$
Commented by Kunal12588 last updated on 13/Mar/19

$${thank}\:{you}\:{sir} \\ $$
