Question Number 56282 by Tawa1 last updated on 13/Mar/19

Commented by mr W last updated on 13/Mar/19
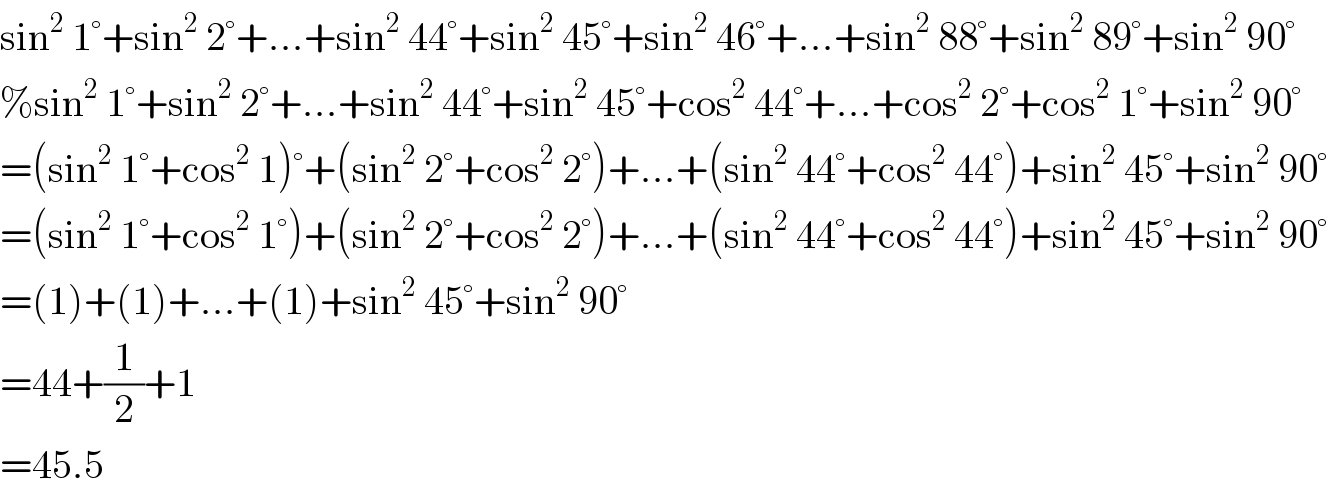
$$\mathrm{sin}^{\mathrm{2}} \:\mathrm{1}°+\mathrm{sin}^{\mathrm{2}} \:\mathrm{2}°+…+\mathrm{sin}^{\mathrm{2}} \:\mathrm{44}°+\mathrm{sin}^{\mathrm{2}} \:\mathrm{45}°+\mathrm{sin}^{\mathrm{2}} \:\mathrm{46}°+…+\mathrm{sin}^{\mathrm{2}} \:\mathrm{88}°+\mathrm{sin}^{\mathrm{2}} \:\mathrm{89}°+\mathrm{sin}^{\mathrm{2}} \:\mathrm{90}° \\ $$$$\%\mathrm{sin}^{\mathrm{2}} \:\mathrm{1}°+\mathrm{sin}^{\mathrm{2}} \:\mathrm{2}°+…+\mathrm{sin}^{\mathrm{2}} \:\mathrm{44}°+\mathrm{sin}^{\mathrm{2}} \:\mathrm{45}°+\mathrm{cos}^{\mathrm{2}} \:\mathrm{44}°+…+\mathrm{cos}^{\mathrm{2}} \:\mathrm{2}°+\mathrm{cos}^{\mathrm{2}} \:\mathrm{1}°+\mathrm{sin}^{\mathrm{2}} \:\mathrm{90}° \\ $$$$=\left(\mathrm{sin}^{\mathrm{2}} \:\mathrm{1}°+\mathrm{cos}^{\mathrm{2}} \:\mathrm{1}\right)°+\left(\mathrm{sin}^{\mathrm{2}} \:\mathrm{2}°+\mathrm{cos}^{\mathrm{2}} \:\mathrm{2}°\right)+…+\left(\mathrm{sin}^{\mathrm{2}} \:\mathrm{44}°+\mathrm{cos}^{\mathrm{2}} \:\mathrm{44}°\right)+\mathrm{sin}^{\mathrm{2}} \:\mathrm{45}°+\mathrm{sin}^{\mathrm{2}} \:\mathrm{90}° \\ $$$$=\left(\mathrm{sin}^{\mathrm{2}} \:\mathrm{1}°+\mathrm{cos}^{\mathrm{2}} \:\mathrm{1}°\right)+\left(\mathrm{sin}^{\mathrm{2}} \:\mathrm{2}°+\mathrm{cos}^{\mathrm{2}} \:\mathrm{2}°\right)+…+\left(\mathrm{sin}^{\mathrm{2}} \:\mathrm{44}°+\mathrm{cos}^{\mathrm{2}} \:\mathrm{44}°\right)+\mathrm{sin}^{\mathrm{2}} \:\mathrm{45}°+\mathrm{sin}^{\mathrm{2}} \:\mathrm{90}° \\ $$$$=\left(\mathrm{1}\right)+\left(\mathrm{1}\right)+…+\left(\mathrm{1}\right)+\mathrm{sin}^{\mathrm{2}} \:\mathrm{45}°+\mathrm{sin}^{\mathrm{2}} \:\mathrm{90}° \\ $$$$=\mathrm{44}+\frac{\mathrm{1}}{\mathrm{2}}+\mathrm{1} \\ $$$$=\mathrm{45}.\mathrm{5} \\ $$
Commented by Tawa1 last updated on 13/Mar/19

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Commented by Tawa1 last updated on 13/Mar/19

$$\mathrm{I}\:\mathrm{want}\:\mathrm{to}\:\mathrm{also}\:\mathrm{understand}\:\mathrm{how}\:\mathrm{he}\:\mathrm{solve}\:\mathrm{using}\:\:\mathrm{complex}\:\mathrm{numbers}.\:\mathrm{please}. \\ $$
Commented by Tawa1 last updated on 13/Mar/19

$$\mathrm{And}\:\mathrm{how}\:\mathrm{he}\:\mathrm{got}\:\mathrm{this}\:\mathrm{step}\:\mathrm{in}\:\mathrm{his}\:\mathrm{solution}:\:\:\:\:\:\left(\frac{\mathrm{1}\:−\:\mathrm{e}^{\mathrm{i}\left(\mathrm{n}\:+\:\mathrm{1}\right)\frac{\pi}{\mathrm{90}}} }{\mathrm{1}\:−\:\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{90}}} }\right) \\ $$
Commented by malwaan last updated on 14/Mar/19

$${very}\:{easy} \\ $$$${thank}\:{you}\:{so}\:{much} \\ $$
