Question Number 56316 by Sr@2004 last updated on 14/Mar/19

Commented by Sr@2004 last updated on 14/Mar/19
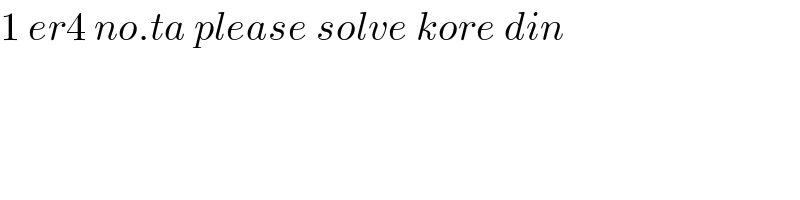
$$\mathrm{1}\:{er}\mathrm{4}\:{no}.{ta}\:{please}\:{solve}\:{kore}\:{din} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 14/Mar/19
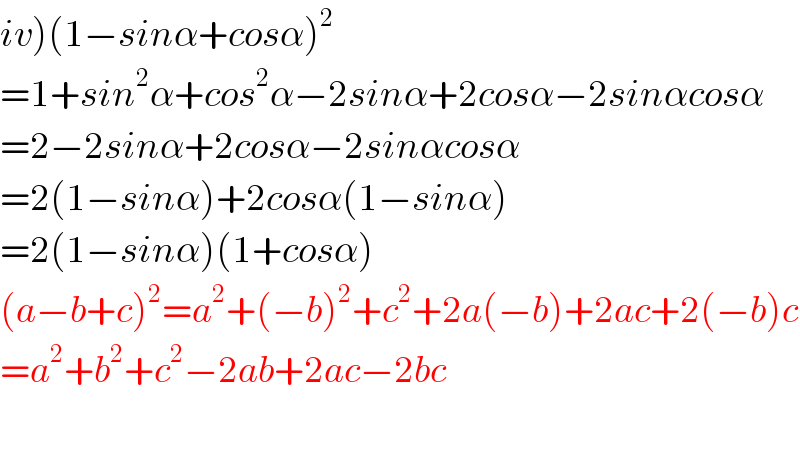
$$\left.{iv}\right)\left(\mathrm{1}−{sin}\alpha+{cos}\alpha\right)^{\mathrm{2}} \\ $$$$=\mathrm{1}+{sin}^{\mathrm{2}} \alpha+{cos}^{\mathrm{2}} \alpha−\mathrm{2}{sin}\alpha+\mathrm{2}{cos}\alpha−\mathrm{2}{sin}\alpha{cos}\alpha \\ $$$$=\mathrm{2}−\mathrm{2}{sin}\alpha+\mathrm{2}{cos}\alpha−\mathrm{2}{sin}\alpha{cos}\alpha \\ $$$$=\mathrm{2}\left(\mathrm{1}−{sin}\alpha\right)+\mathrm{2}{cos}\alpha\left(\mathrm{1}−{sin}\alpha\right) \\ $$$$=\mathrm{2}\left(\mathrm{1}−{sin}\alpha\right)\left(\mathrm{1}+{cos}\alpha\right) \\ $$$$\left({a}−{b}+{c}\right)^{\mathrm{2}} ={a}^{\mathrm{2}} +\left(−{b}\right)^{\mathrm{2}} +{c}^{\mathrm{2}} +\mathrm{2}{a}\left(−{b}\right)+\mathrm{2}{ac}+\mathrm{2}\left(−{b}\right){c} \\ $$$$={a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} −\mathrm{2}{ab}+\mathrm{2}{ac}−\mathrm{2}{bc} \\ $$$$ \\ $$
