Menu Close

Question-56383

Tinku Tara 0 Comments
Pin




Question Number 56383 by Tawa1 last updated on 15/Mar/19
Commented by Tawa1 last updated on 16/Mar/19
God bless you sir
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Commented by maxmathsup by imad last updated on 15/Mar/19
∫_(−1) ^7 (dx/((^3 (√(x+1)))))dx =_(x+1 =t^3 ) ∫_0 ^(2(√2)) ((3t^2 dt)/t) =3 ∫_0 ^(2(√2)) tdt =3[(t^2 /2)]_0 ^(2(√2)) =(3/2){2(√2))^2 =12.
$$\int_{−\mathrm{1}} ^{\mathrm{7}} \:\:\frac{{dx}}{\left(^{\mathrm{3}} \sqrt{{x}+\mathrm{1}}\right)}{dx}\:=_{{x}+\mathrm{1}\:={t}^{\mathrm{3}} } \:\:\:\int_{\mathrm{0}} ^{\mathrm{2}\sqrt{\mathrm{2}}} \:\:\:\frac{\mathrm{3}{t}^{\mathrm{2}} {dt}}{{t}}\:=\mathrm{3}\:\int_{\mathrm{0}} ^{\mathrm{2}\sqrt{\mathrm{2}}} {tdt}\:=\mathrm{3}\left[\frac{{t}^{\mathrm{2}} }{\mathrm{2}}\right]_{\mathrm{0}} ^{\mathrm{2}\sqrt{\mathrm{2}}} \\ $$$$=\frac{\mathrm{3}}{\mathrm{2}}\left\{\mathrm{2}\sqrt{\mathrm{2}}\right)^{\mathrm{2}} \:=\mathrm{12}. \\ $$
Commented by maxmathsup by imad last updated on 16/Mar/19
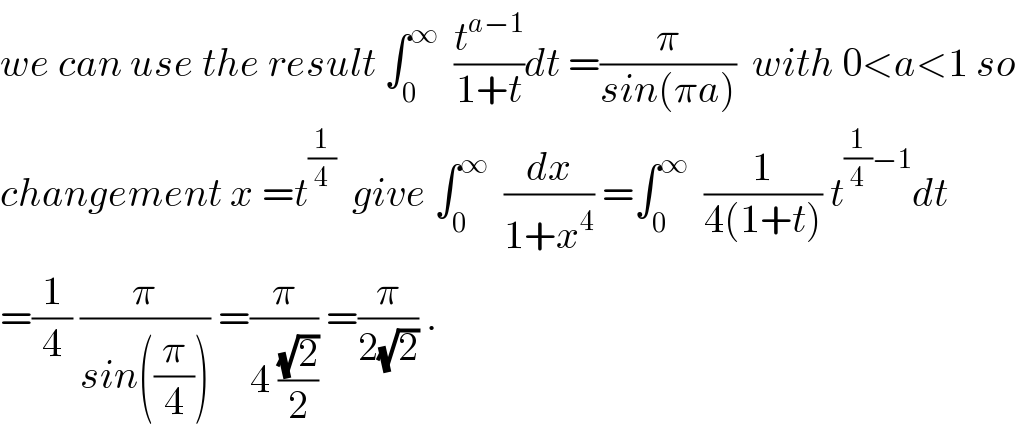
we can use the result ∫_0 ^∞ (t^(a−1) /(1+t))dt =(π/(sin(πa))) with 0<a<1 so changement x =t^(1/4) give ∫_0 ^∞ (dx/(1+x^4 )) =∫_0 ^∞ (1/(4(1+t))) t^((1/4)−1) dt =(1/4) (π/(sin((π/4)))) =(π/(4 ((√2)/2))) =(π/(2(√2))) .
$${we}\:{can}\:{use}\:{the}\:{result}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{t}^{{a}−\mathrm{1}} }{\mathrm{1}+{t}}{dt}\:=\frac{\pi}{{sin}\left(\pi{a}\right)}\:\:{with}\:\mathrm{0}<{a}<\mathrm{1}\:{so} \\ $$$${changement}\:{x}\:={t}^{\frac{\mathrm{1}}{\mathrm{4}}} \:\:{give}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{dx}}{\mathrm{1}+{x}^{\mathrm{4}} }\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{1}}{\mathrm{4}\left(\mathrm{1}+{t}\right)}\:{t}^{\frac{\mathrm{1}}{\mathrm{4}}−\mathrm{1}} {dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\:\frac{\pi}{{sin}\left(\frac{\pi}{\mathrm{4}}\right)}\:=\frac{\pi}{\mathrm{4}\:\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}}\:=\frac{\pi}{\mathrm{2}\sqrt{\mathrm{2}}}\:. \\ $$
Commented by Abdo msup. last updated on 16/Mar/19
thank you so much sir.
$${thank}\:{you}\:{so}\:{much}\:{sir}. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 15/Mar/19
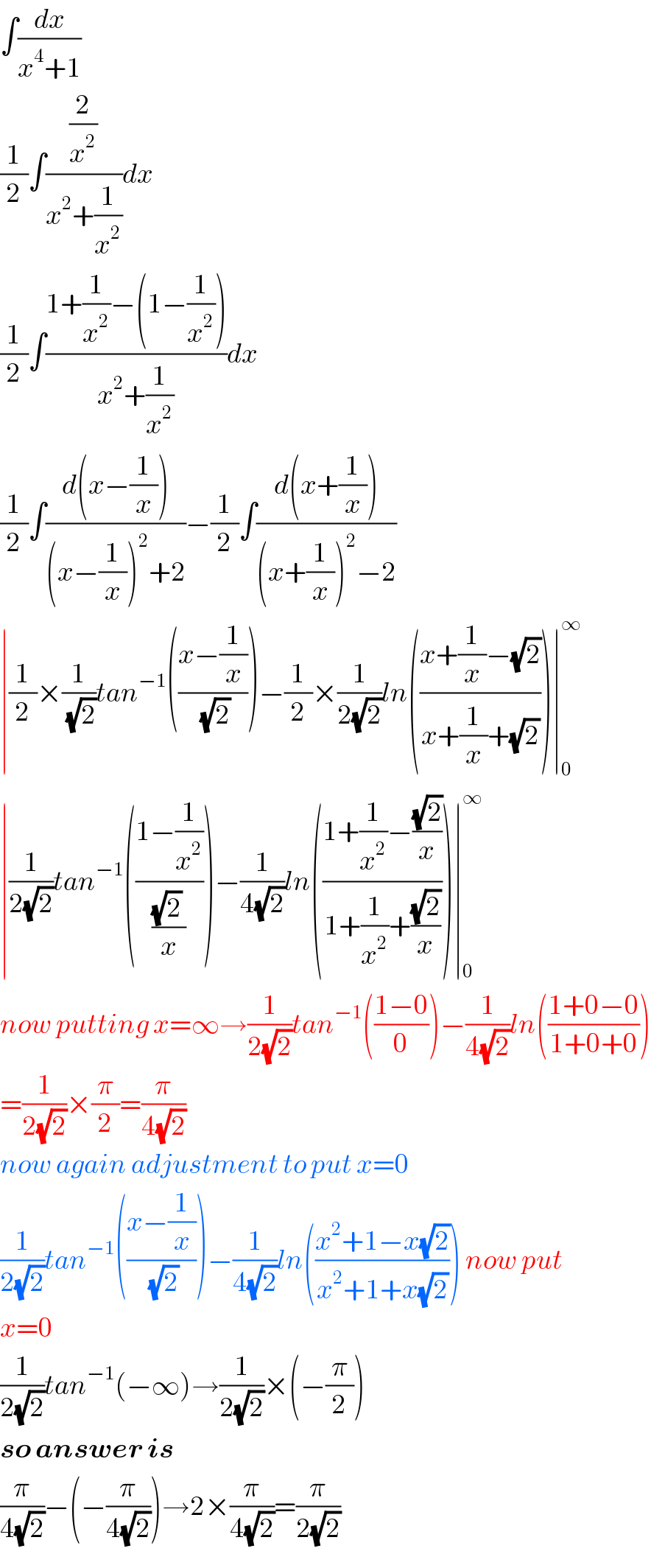
∫(dx/(x^4 +1)) (1/2)∫((2/x^2 )/(x^2 +(1/x^2 )))dx (1/2)∫((1+(1/x^2 )−(1−(1/x^2 )))/(x^2 +(1/x^2 )))dx (1/2)∫((d(x−(1/x)))/((x−(1/x))^2 +2))−(1/2)∫((d(x+(1/x)))/((x+(1/x))^2 −2)) ∣(1/2)×(1/( (√2)))tan^(−1) (((x−(1/x))/( (√2))))−(1/2)×(1/(2(√2)))ln(((x+(1/x)−(√2))/(x+(1/x)+(√2))))∣_0 ^∞ ∣(1/(2(√2)))tan^(−1) (((1−(1/x^2 ))/(((√2) )/x)))−(1/(4(√2)))ln(((1+(1/x^2 )−((√2)/x))/(1+(1/x^2 )+((√2)/x))))∣_0 ^∞ now putting x=∞→(1/(2(√2)))tan^(−1) (((1−0)/0))−(1/(4(√2)))ln(((1+0−0)/(1+0+0))) =(1/(2(√2)))×(π/2)=(π/(4(√2))) now again adjustment to put x=0 (1/(2(√2)))tan^(−1) (((x−(1/x))/( (√2))))−(1/(4(√2)))ln(((x^2 +1−x(√2))/(x^2 +1+x(√2)))) now put x=0 (1/(2(√2)))tan^(−1) (−∞)→(1/(2(√2)))×(−(π/2)) so answer is (π/(4(√2)))−(−(π/(4(√2))))→2×(π/(4(√2)))=(π/(2(√2)))
$$\int\frac{{dx}}{{x}^{\mathrm{4}} +\mathrm{1}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\frac{\mathrm{2}}{{x}^{\mathrm{2}} }}{{x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}{dx} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }−\left(\mathrm{1}−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)}{{x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}{dx} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{d}\left({x}−\frac{\mathrm{1}}{{x}}\right)}{\left({x}−\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} +\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{d}\left({x}+\frac{\mathrm{1}}{{x}}\right)}{\left({x}+\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} −\mathrm{2}} \\ $$$$\mid\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}{tan}^{−\mathrm{1}} \left(\frac{{x}−\frac{\mathrm{1}}{{x}}}{\:\sqrt{\mathrm{2}}}\right)−\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}{ln}\left(\frac{{x}+\frac{\mathrm{1}}{{x}}−\sqrt{\mathrm{2}}}{{x}+\frac{\mathrm{1}}{{x}}+\sqrt{\mathrm{2}}}\right)\mid_{\mathrm{0}} ^{\infty} \\ $$$$\mid\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}{tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}{\frac{\sqrt{\mathrm{2}}\:}{{x}}}\right)−\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{2}}}{ln}\left(\frac{\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }−\frac{\sqrt{\mathrm{2}}}{{x}}}{\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }+\frac{\sqrt{\mathrm{2}}}{{x}}}\right)\mid_{\mathrm{0}} ^{\infty} \\ $$$${now}\:{putting}\:{x}=\infty\rightarrow\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}{tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}−\mathrm{0}}{\mathrm{0}}\right)−\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{2}}}{ln}\left(\frac{\mathrm{1}+\mathrm{0}−\mathrm{0}}{\mathrm{1}+\mathrm{0}+\mathrm{0}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}×\frac{\pi}{\mathrm{2}}=\frac{\pi}{\mathrm{4}\sqrt{\mathrm{2}}} \\ $$$${now}\:{again}\:{adjustment}\:{to}\:{put}\:{x}=\mathrm{0} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}{tan}^{−\mathrm{1}} \left(\frac{{x}−\frac{\mathrm{1}}{{x}}}{\:\sqrt{\mathrm{2}}}\right)−\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{2}}}{ln}\left(\frac{{x}^{\mathrm{2}} +\mathrm{1}−{x}\sqrt{\mathrm{2}}}{{x}^{\mathrm{2}} +\mathrm{1}+{x}\sqrt{\mathrm{2}}}\right)\:{now}\:{put} \\ $$$${x}=\mathrm{0} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}{tan}^{−\mathrm{1}} \left(−\infty\right)\rightarrow\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}×\left(−\frac{\pi}{\mathrm{2}}\right) \\ $$$$\boldsymbol{{so}}\:\boldsymbol{{answer}}\:\boldsymbol{{is}} \\ $$$$\frac{\pi}{\mathrm{4}\sqrt{\mathrm{2}}}−\left(−\frac{\pi}{\mathrm{4}\sqrt{\mathrm{2}}}\right)\rightarrow\mathrm{2}×\frac{\pi}{\mathrm{4}\sqrt{\mathrm{2}}}=\frac{\pi}{\mathrm{2}\sqrt{\mathrm{2}}} \\ $$
Commented by Tawa1 last updated on 15/Mar/19
God bless you sir
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 15/Mar/19
lim_(a→−1) ∫_a ^7 (dx/((1+x)^(1/3) )) lim_(a→−1) ∣(((1+x)^(((−1)/3)+1) )/(2/3))∣_a ^7 =lim_(a→−1) [(3/2)(8)^(2/3) −(3/2)(1+a)^(2/3) ] =(3/2)×4→6 ans
$$\underset{{a}\rightarrow−\mathrm{1}} {\mathrm{lim}}\int_{{a}} ^{\mathrm{7}} \frac{{dx}}{\left(\mathrm{1}+{x}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} } \\ $$$$\underset{{a}\rightarrow−\mathrm{1}} {\mathrm{lim}}\mid\frac{\left(\mathrm{1}+{x}\right)^{\frac{−\mathrm{1}}{\mathrm{3}}+\mathrm{1}} }{\frac{\mathrm{2}}{\mathrm{3}}}\mid_{{a}} ^{\mathrm{7}} \\ $$$$=\underset{{a}\rightarrow−\mathrm{1}} {\mathrm{lim}}\left[\frac{\mathrm{3}}{\mathrm{2}}\left(\mathrm{8}\right)^{\frac{\mathrm{2}}{\mathrm{3}}} −\frac{\mathrm{3}}{\mathrm{2}}\left(\mathrm{1}+{a}\right)^{\frac{\mathrm{2}}{\mathrm{3}}} \right] \\ $$$$=\frac{\mathrm{3}}{\mathrm{2}}×\mathrm{4}\rightarrow\mathrm{6}\:{ans} \\ $$
Commented by Tawa1 last updated on 15/Mar/19
God bless you sir.
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *