Question Number 56390 by Tinkutara last updated on 15/Mar/19

Commented by Tinkutara last updated on 18/Mar/19
Answer is
Commented by Tinkutara last updated on 18/Mar/19
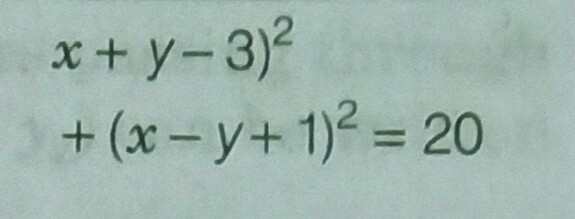
Answered by tanmay.chaudhury50@gmail.com last updated on 16/Mar/19
![A(1,2) B((√(5 )) cosθ,(√5) sinθ) C((√5) sinθ,−(√5) cosθ) slope of AB →m_1 =(((√5) sinθ−2)/( (√5) cosθ−1)) slope BC→m_2 =(((√5) sinθ+(√5) cosθ)/( (√5) cosθ−(√5) sinθ))=((1+tanθ)/(1−tanθ))=tan((π/4)+θ) slope of CA→m_3 =((2+(√5) cosθ)/(1−(√5) sinθ)) eqn st line ⊥BC and passing through eqn AD⊥BC (y−2)=(((−1)/m_2 ))(x−1) (y−2)=(((tanθ−1)/(tanθ+1)))(x−1) eqn BE⊥AC (y−(√5) sinθ)=−((1/m_3 ))(x−(√5) cosθ) (y−(√5) sinθ)=((((√5) sinθ−1)/(2+(√5) cosθ)))(x−(√5) cosθ) solving eqn AD and BE we get ortho centre 2+(((tanθ−1)/(tanθ+1)))(x−1)=(√5) sinθ+((((√5) sinθ−1)/(2+(√5) cosθ)))(x−(√5) cosθ) for easy of simplificatiin (√5) sinθ=a (√5) cosθ=b tanθ=(a/b) 2+((((a/b)−1)/((a/b)+1)))(x−1)=a+(((a−1)/(2+b)))(x−b) 2+x(((a−b)/(a+b)))−(((a−b)/(a+b)))=a+x(((a−1)/(2+b)))−b(((a−1)/(2+b))) x{(((a−b)/(a+b)))−(((a−1)/(2+b)))}=a−b(((a−1)/(2+b)))−2+((a−b)/(a+b)) x{((2a−2b+ab−b^2 −a^2 −ab+a+b)/((a+b)(2+b))}=((a(2a+2b+ab+b^2 )−b(a^2 +ab−a−b)−2(2a+2b+ab+b^2 )+(2a+ab−2b−b^2 ))/((2+b)(a+b))) x(3a−b−b^2 −a^2 )=4a+4b+a^2 b+ab^2 −a^2 b−ab^2 +ab+b^2 −4a−4b−2ab−b^2 +2a+ab−2b−b^2 x(3a−b−b^2 −a^2 )=2a−2b+ab+b^2 −2ab−b^2 +ab−b^2 x(3a−b−b^2 −a^2 )=2a−2b−b^2 x=((2a−2b−b^2 )/(3a−b−a^2 −b^2 )) [a=(√5) sinθ b=(√5) cosθ] pls check upto this lengthy question...](https://www.tinkutara.com/question/Q56428.png)
$${A}\left(\mathrm{1},\mathrm{2}\right)\:\:{B}\left(\sqrt{\mathrm{5}\:}\:{cos}\theta,\sqrt{\mathrm{5}}\:{sin}\theta\right)\:\:{C}\left(\sqrt{\mathrm{5}}\:{sin}\theta,−\sqrt{\mathrm{5}}\:{cos}\theta\right) \\ $$$${slope}\:{of}\:{AB}\:\rightarrow{m}_{\mathrm{1}} =\frac{\sqrt{\mathrm{5}}\:{sin}\theta−\mathrm{2}}{\:\sqrt{\mathrm{5}}\:{cos}\theta−\mathrm{1}} \\ $$$${slope}\:{BC}\rightarrow{m}_{\mathrm{2}} =\frac{\sqrt{\mathrm{5}}\:{sin}\theta+\sqrt{\mathrm{5}}\:{cos}\theta}{\:\sqrt{\mathrm{5}}\:{cos}\theta−\sqrt{\mathrm{5}}\:{sin}\theta}=\frac{\mathrm{1}+{tan}\theta}{\mathrm{1}−{tan}\theta}={tan}\left(\frac{\pi}{\mathrm{4}}+\theta\right) \\ $$$${slope}\:{of}\:{CA}\rightarrow{m}_{\mathrm{3}} =\frac{\mathrm{2}+\sqrt{\mathrm{5}}\:{cos}\theta}{\mathrm{1}−\sqrt{\mathrm{5}}\:{sin}\theta} \\ $$$${eqn}\:{st}\:{line}\:\bot{BC}\:{and}\:{passing}\:{through} \\ $$$${eqn}\:{AD}\bot{BC}\:\:\left({y}−\mathrm{2}\right)=\left(\frac{−\mathrm{1}}{{m}_{\mathrm{2}} }\right)\left({x}−\mathrm{1}\right) \\ $$$$\left({y}−\mathrm{2}\right)=\left(\frac{{tan}\theta−\mathrm{1}}{{tan}\theta+\mathrm{1}}\right)\left({x}−\mathrm{1}\right) \\ $$$${eqn}\:{BE}\bot{AC} \\ $$$$\left({y}−\sqrt{\mathrm{5}}\:{sin}\theta\right)=−\left(\frac{\mathrm{1}}{{m}_{\mathrm{3}} }\right)\left({x}−\sqrt{\mathrm{5}}\:{cos}\theta\right) \\ $$$$\left({y}−\sqrt{\mathrm{5}}\:{sin}\theta\right)=\left(\frac{\sqrt{\mathrm{5}}\:{sin}\theta−\mathrm{1}}{\mathrm{2}+\sqrt{\mathrm{5}}\:{cos}\theta}\right)\left({x}−\sqrt{\mathrm{5}}\:{cos}\theta\right) \\ $$$${solving}\:{eqn}\:{AD}\:{and}\:{BE}\:{we}\:{get}\:{ortho}\:{centre} \\ $$$$\mathrm{2}+\left(\frac{{tan}\theta−\mathrm{1}}{{tan}\theta+\mathrm{1}}\right)\left({x}−\mathrm{1}\right)=\sqrt{\mathrm{5}}\:{sin}\theta+\left(\frac{\sqrt{\mathrm{5}}\:{sin}\theta−\mathrm{1}}{\mathrm{2}+\sqrt{\mathrm{5}}\:{cos}\theta}\right)\left({x}−\sqrt{\mathrm{5}}\:{cos}\theta\right) \\ $$$${for}\:{easy}\:{of}\:{simplificatiin}\:\sqrt{\mathrm{5}}\:{sin}\theta={a} \\ $$$$\sqrt{\mathrm{5}}\:{cos}\theta={b}\:\:\:{tan}\theta=\frac{{a}}{{b}} \\ $$$$\mathrm{2}+\left(\frac{\frac{{a}}{{b}}−\mathrm{1}}{\frac{{a}}{{b}}+\mathrm{1}}\right)\left({x}−\mathrm{1}\right)={a}+\left(\frac{{a}−\mathrm{1}}{\mathrm{2}+{b}}\right)\left({x}−{b}\right) \\ $$$$\mathrm{2}+{x}\left(\frac{{a}−{b}}{{a}+{b}}\right)−\left(\frac{{a}−{b}}{{a}+{b}}\right)={a}+{x}\left(\frac{{a}−\mathrm{1}}{\mathrm{2}+{b}}\right)−{b}\left(\frac{{a}−\mathrm{1}}{\mathrm{2}+{b}}\right) \\ $$$${x}\left\{\left(\frac{{a}−{b}}{{a}+{b}}\right)−\left(\frac{{a}−\mathrm{1}}{\mathrm{2}+{b}}\right)\right\}={a}−{b}\left(\frac{{a}−\mathrm{1}}{\mathrm{2}+{b}}\right)−\mathrm{2}+\frac{{a}−{b}}{{a}+{b}} \\ $$$${x}\left\{\frac{\mathrm{2}{a}−\mathrm{2}{b}+{ab}−{b}^{\mathrm{2}} −{a}^{\mathrm{2}} −{ab}+{a}+{b}}{\left({a}+{b}\right)\left(\mathrm{2}+{b}\right.}\right\}=\frac{{a}\left(\mathrm{2}{a}+\mathrm{2}{b}+{ab}+{b}^{\mathrm{2}} \right)−{b}\left({a}^{\mathrm{2}} +{ab}−{a}−{b}\right)−\mathrm{2}\left(\mathrm{2}{a}+\mathrm{2}{b}+{ab}+{b}^{\mathrm{2}} \right)+\left(\mathrm{2}{a}+{ab}−\mathrm{2}{b}−{b}^{\mathrm{2}} \right)}{\left(\mathrm{2}+{b}\right)\left({a}+{b}\right)} \\ $$$${x}\left(\mathrm{3}{a}−{b}−{b}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)=\mathrm{4}{a}+\mathrm{4}{b}+{a}^{\mathrm{2}} {b}+{ab}^{\mathrm{2}} −{a}^{\mathrm{2}} {b}−{ab}^{\mathrm{2}} +{ab}+{b}^{\mathrm{2}} −\mathrm{4}{a}−\mathrm{4}{b}−\mathrm{2}{ab}−{b}^{\mathrm{2}} +\mathrm{2}{a}+{ab}−\mathrm{2}{b}−{b}^{\mathrm{2}} \\ $$$${x}\left(\mathrm{3}{a}−{b}−{b}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)=\mathrm{2}{a}−\mathrm{2}{b}+{ab}+{b}^{\mathrm{2}} −\mathrm{2}{ab}−{b}^{\mathrm{2}} +{ab}−{b}^{\mathrm{2}} \\ $$$${x}\left(\mathrm{3}{a}−{b}−{b}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)=\mathrm{2}{a}−\mathrm{2}{b}−{b}^{\mathrm{2}} \\ $$$${x}=\frac{\mathrm{2}{a}−\mathrm{2}{b}−{b}^{\mathrm{2}} }{\mathrm{3}{a}−{b}−{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }\:\:\left[{a}=\sqrt{\mathrm{5}}\:{sin}\theta\:\:\:{b}=\sqrt{\mathrm{5}}\:{cos}\theta\right] \\ $$$${pls}\:{check}\:{upto}\:{this}\:{lengthy}\:{question}… \\ $$
