Question-56461

Question Number 56461 by cesar.marval.larez@gmail.com last updated on 16/Mar/19

Answered by tanmay.chaudhury50@gmail.com last updated on 17/Mar/19

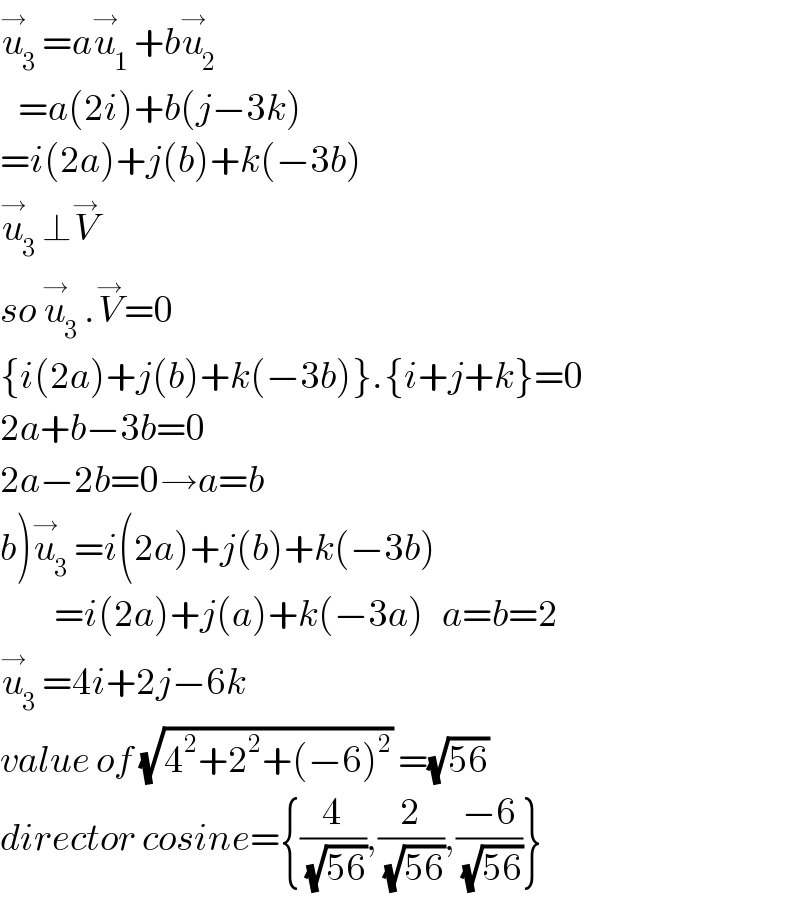
u_3 ^→ =au_1 ^→ +bu_2 ^→ =a(2i)+b(j−3k) =i(2a)+j(b)+k(−3b) u_3 ^→ ⊥V^→ so u_3 ^→ .V^→ =0 {i(2a)+j(b)+k(−3b)}.{i+j+k}=0 2a+b−3b=0 2a−2b=0→a=b b)u_3 ^→ =i(2a)+j(b)+k(−3b) =i(2a)+j(a)+k(−3a) a=b=2 u_3 ^→ =4i+2j−6k value of (√(4^2 +2^2 +(−6)^2 )) =(√(56)) director cosine={(4/( (√(56)))),(2/( (√(56)))),((−6)/( (√(56))))}

$$\overset{\rightarrow} {{u}}_{\mathrm{3}} ={a}\overset{\rightarrow} {{u}}_{\mathrm{1}} +{b}\overset{\rightarrow} {{u}}_{\mathrm{2}} \\ $$$$\:\:\:={a}\left(\mathrm{2}{i}\right)+{b}\left({j}−\mathrm{3}{k}\right) \\ $$$$={i}\left(\mathrm{2}{a}\right)+{j}\left({b}\right)+{k}\left(−\mathrm{3}{b}\right) \\ $$$$\overset{\rightarrow} {{u}}_{\mathrm{3}} \bot\overset{\rightarrow} {{V}} \\ $$$${so}\:\overset{\rightarrow} {{u}}_{\mathrm{3}} .\overset{\rightarrow} {{V}}=\mathrm{0} \\ $$$$\left\{{i}\left(\mathrm{2}{a}\right)+{j}\left({b}\right)+{k}\left(−\mathrm{3}{b}\right)\right\}.\left\{{i}+{j}+{k}\right\}=\mathrm{0} \\ $$$$\mathrm{2}{a}+{b}−\mathrm{3}{b}=\mathrm{0} \\ $$$$\mathrm{2}{a}−\mathrm{2}{b}=\mathrm{0}\rightarrow{a}={b} \\ $$$$\left.{b}\right)\overset{\rightarrow} {{u}}_{\mathrm{3}} ={i}\left(\mathrm{2}{a}\right)+{j}\left({b}\right)+{k}\left(−\mathrm{3}{b}\right) \\ $$$$\:\:\:\:\:\:\:\:\:={i}\left(\mathrm{2}{a}\right)+{j}\left({a}\right)+{k}\left(−\mathrm{3}{a}\right)\:\:\:{a}={b}=\mathrm{2} \\ $$$$\overset{\rightarrow} {{u}}_{\mathrm{3}} =\mathrm{4}{i}+\mathrm{2}{j}−\mathrm{6}{k} \\ $$$${value}\:{of}\:\sqrt{\mathrm{4}^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} +\left(−\mathrm{6}\right)^{\mathrm{2}} }\:=\sqrt{\mathrm{56}}\: \\ $$$${director}\:{cosine}=\left\{\frac{\mathrm{4}}{\:\sqrt{\mathrm{56}}},\frac{\mathrm{2}}{\:\sqrt{\mathrm{56}}},\frac{−\mathrm{6}}{\:\sqrt{\mathrm{56}}}\right\} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply