Menu Close

Question-56471

Tinku Tara 0 Comments
Pin




Question Number 56471 by harish 12@g last updated on 17/Mar/19
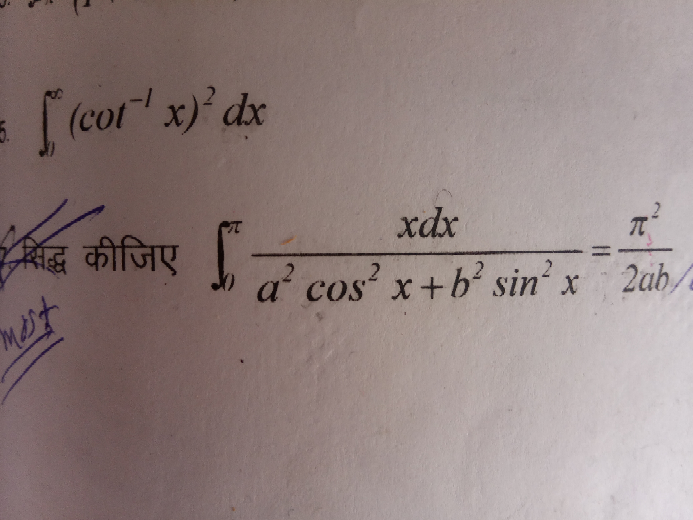
Answered by tanmay.chaudhury50@gmail.com last updated on 17/Mar/19
∫_0 ^π ((xdx)/(a^2 cos^2 x+b^2 sin^2 x))dx=I I=∫_0 ^π (((π−x))/(a^2 cos^2 (π−x)+b^2 sin^2 (π−x)))dx =∫_0 ^π ((π−x)/(a^2 cos^2 x+b^2 sin^2 x))dx 2I=∫_0 ^π ((π−x+x)/(a^2 cos^2 x+b^2 sin^2 x))dx ((2I)/π)=∫_0 ^π (dx/(cos^2 x(a^2 +b^2 tan^2 x)))dx ((2I)/π)=∫_0 ^π ((sec^2 xdx)/(a^2 +b^2 tan^2 x))dx ((2I)/π)=(1/b^2 )∫_0 ^π ((sec^2 xdx)/(((a/b))^2 +tan^2 x))dx now ∫_0 ^(2a) f(x)dx=2∫_0 ^a f(x)dx when f(2a−x)=f(x) ((2I)/π)=(2/b^2 )∫_0 ^(π/2) ((sec^2 xdx)/(((a/b))^2 +tan^2 x))dx tanx=(a/b)tanp sec^2 xdx=(a/b)sec^2 pdp ((b^2 I)/π)=∫_0 ^(π/2) (((a/b)sec^2 p)/(((a^2 /b^2 ))(1+tan^2 p)))dp ((b^2 I)/π)=(b/a)∫_0 ^(π/2) dp ((abI)/π)=∣p∣_0 ^(π/2) ((abI)/π)=(π/2) so I=(π^2 /(2ab)) proved
$$\int_{\mathrm{0}} ^{\pi} \frac{{xdx}}{{a}^{\mathrm{2}} {cos}^{\mathrm{2}} {x}+{b}^{\mathrm{2}} {sin}^{\mathrm{2}} {x}}{dx}={I} \\ $$$${I}=\int_{\mathrm{0}} ^{\pi} \frac{\left(\pi−{x}\right)}{{a}^{\mathrm{2}} {cos}^{\mathrm{2}} \left(\pi−{x}\right)+{b}^{\mathrm{2}} {sin}^{\mathrm{2}} \left(\pi−{x}\right)}{dx} \\ $$$$=\int_{\mathrm{0}} ^{\pi} \frac{\pi−{x}}{{a}^{\mathrm{2}} {cos}^{\mathrm{2}} {x}+{b}^{\mathrm{2}} {sin}^{\mathrm{2}} {x}}{dx} \\ $$$$\mathrm{2}{I}=\int_{\mathrm{0}} ^{\pi} \frac{\pi−{x}+{x}}{{a}^{\mathrm{2}} {cos}^{\mathrm{2}} {x}+{b}^{\mathrm{2}} {sin}^{\mathrm{2}} {x}}{dx} \\ $$$$\frac{\mathrm{2}{I}}{\pi}=\int_{\mathrm{0}} ^{\pi} \frac{{dx}}{{cos}^{\mathrm{2}} {x}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} {tan}^{\mathrm{2}} {x}\right)}{dx} \\ $$$$\frac{\mathrm{2}{I}}{\pi}=\int_{\mathrm{0}} ^{\pi} \frac{{sec}^{\mathrm{2}} {xdx}}{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} {tan}^{\mathrm{2}} {x}}{dx} \\ $$$$\frac{\mathrm{2}{I}}{\pi}=\frac{\mathrm{1}}{{b}^{\mathrm{2}} }\int_{\mathrm{0}} ^{\pi} \frac{{sec}^{\mathrm{2}} {xdx}}{\left(\frac{{a}}{{b}}\right)^{\mathrm{2}} +{tan}^{\mathrm{2}} {x}}{dx} \\ $$$${now}\:\:\int_{\mathrm{0}} ^{\mathrm{2}{a}} {f}\left({x}\right){dx}=\mathrm{2}\int_{\mathrm{0}} ^{{a}} {f}\left({x}\right){dx}\:\:{when}\:{f}\left(\mathrm{2}{a}−{x}\right)={f}\left({x}\right) \\ $$$$\frac{\mathrm{2}{I}}{\pi}=\frac{\mathrm{2}}{{b}^{\mathrm{2}} }\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{sec}^{\mathrm{2}} {xdx}}{\left(\frac{{a}}{{b}}\right)^{\mathrm{2}} +{tan}^{\mathrm{2}} {x}}{dx} \\ $$$${tanx}=\frac{{a}}{{b}}{tanp}\:\: \\ $$$${sec}^{\mathrm{2}} {xdx}=\frac{{a}}{{b}}{sec}^{\mathrm{2}} {pdp} \\ $$$$\frac{{b}^{\mathrm{2}} {I}}{\pi}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\frac{{a}}{{b}}{sec}^{\mathrm{2}} {p}}{\left(\frac{{a}^{\mathrm{2}} }{{b}^{\mathrm{2}} }\right)\left(\mathrm{1}+{tan}^{\mathrm{2}} {p}\right)}{dp} \\ $$$$\frac{{b}^{\mathrm{2}} {I}}{\pi}=\frac{{b}}{{a}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {dp} \\ $$$$\frac{{abI}}{\pi}=\mid{p}\mid_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \\ $$$$\frac{{abI}}{\pi}=\frac{\pi}{\mathrm{2}} \\ $$$${so}\:{I}=\frac{\pi^{\mathrm{2}} }{\mathrm{2}{ab}}\:\:{proved} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *