Question Number 56481 by Gulay last updated on 17/Mar/19

Commented by Gulay last updated on 17/Mar/19

$$\mathrm{sir}\:\mathrm{plz}\:\mathrm{help}\:\mathrm{me} \\ $$$$ \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 17/Mar/19
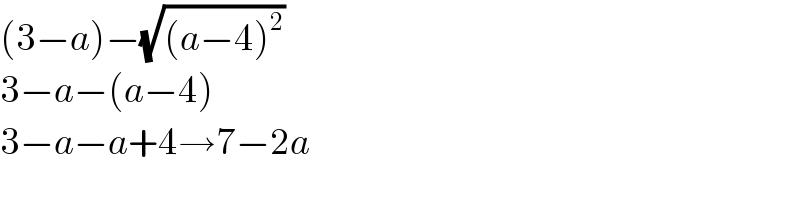
$$\left(\mathrm{3}−{a}\right)−\sqrt{\left({a}−\mathrm{4}\right)^{\mathrm{2}} }\: \\ $$$$\mathrm{3}−{a}−\left({a}−\mathrm{4}\right) \\ $$$$\mathrm{3}−{a}−{a}+\mathrm{4}\rightarrow\mathrm{7}−\mathrm{2}{a} \\ $$
Commented by Gulay last updated on 17/Mar/19

$$\mathrm{thanks}\:\mathrm{sir} \\ $$
Commented by 121194 last updated on 17/Mar/19
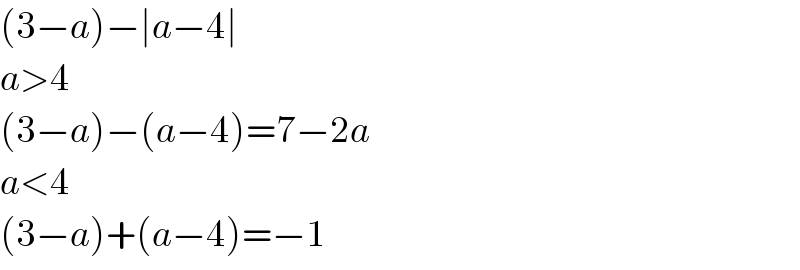
$$\left(\mathrm{3}−{a}\right)−\mid{a}−\mathrm{4}\mid \\ $$$${a}>\mathrm{4} \\ $$$$\left(\mathrm{3}−{a}\right)−\left({a}−\mathrm{4}\right)=\mathrm{7}−\mathrm{2}{a} \\ $$$${a}<\mathrm{4} \\ $$$$\left(\mathrm{3}−{a}\right)+\left({a}−\mathrm{4}\right)=−\mathrm{1} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 17/Mar/19

Commented by tanmay.chaudhury50@gmail.com last updated on 17/Mar/19

Answered by kaivan.ahmadi last updated on 17/Mar/19
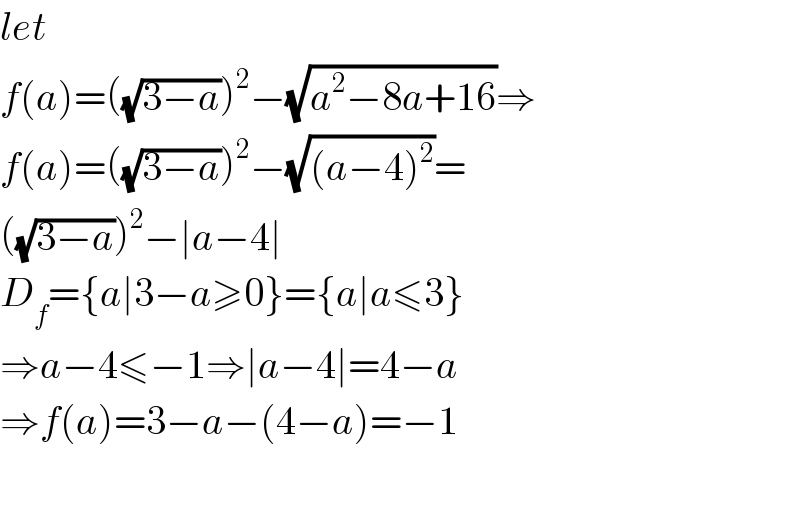
$${let} \\ $$$${f}\left({a}\right)=\left(\sqrt{\mathrm{3}−{a}}\right)^{\mathrm{2}} −\sqrt{{a}^{\mathrm{2}} −\mathrm{8}{a}+\mathrm{16}}\Rightarrow \\ $$$${f}\left({a}\right)=\left(\sqrt{\mathrm{3}−{a}}\right)^{\mathrm{2}} −\sqrt{\left({a}−\mathrm{4}\right)^{\mathrm{2}} }= \\ $$$$\left(\sqrt{\mathrm{3}−{a}}\right)^{\mathrm{2}} −\mid{a}−\mathrm{4}\mid \\ $$$${D}_{{f}} =\left\{{a}\mid\mathrm{3}−{a}\geqslant\mathrm{0}\right\}=\left\{{a}\mid{a}\leqslant\mathrm{3}\right\} \\ $$$$\Rightarrow{a}−\mathrm{4}\leqslant−\mathrm{1}\Rightarrow\mid{a}−\mathrm{4}\mid=\mathrm{4}−{a} \\ $$$$\Rightarrow{f}\left({a}\right)=\mathrm{3}−{a}−\left(\mathrm{4}−{a}\right)=−\mathrm{1} \\ $$$$ \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 17/Mar/19

Commented by tanmay.chaudhury50@gmail.com last updated on 17/Mar/19

Commented by 121194 last updated on 18/Mar/19

$$\left(\sqrt{−\mathrm{1}}\right)^{\mathrm{2}} ={i}^{\mathrm{2}} =−\mathrm{1} \\ $$$$\sqrt{\left(−\mathrm{1}\right)^{\mathrm{2}} }=\sqrt{\mathrm{1}}=\mathrm{1}=\mid−\mathrm{1}\mid \\ $$
Commented by MJS last updated on 19/Mar/19

$$\sqrt[{{n}}]{{x}}\:\mathrm{always}\:\mathrm{means}\:\mathrm{the}\:\mathrm{principal}\:\mathrm{value} \\ $$$$\mathrm{we}\:\mathrm{don}'\mathrm{t}\:\mathrm{solve}\:\mathrm{for}\:\mathrm{anything}\:\mathrm{writing} \\ $$$$\mathrm{4}+\sqrt{\mathrm{2}},\:\sqrt[{\mathrm{3}}]{\mathrm{3}}−\sqrt[{\mathrm{6}}]{\mathrm{5}}\mathrm{i},\:… \\ $$$$\mathrm{solving},\:\mathrm{we}\:\mathrm{look}\:\mathrm{for}\:{all}\:{possible}\:\mathrm{values}: \\ $$$$\sqrt{{x}}=\mathrm{3}\:\Rightarrow\:{x}=\mathrm{9}\:\mathrm{without}\:\mathrm{any}\:\mathrm{doubt}\:\mathrm{for}\:{x}\in\mathbb{C} \\ $$$$\mathrm{also}\:\sqrt[{\mathrm{3}}]{−{x}}=\mathrm{2}\:\Rightarrow\:{x}=−\mathrm{8} \\ $$$${y}=−\sqrt{\mathrm{5}}\:\Rightarrow\:\mathrm{nothing}\:\mathrm{to}\:\mathrm{solve} \\ $$$$\mathrm{but} \\ $$$${z}^{\mathrm{2}} =\mathrm{7}\:\Rightarrow\:{z}=−\sqrt{\mathrm{7}}\vee{z}=\sqrt{\mathrm{7}} \\ $$$${z}^{\mathrm{3}} =\mathrm{11}\:\Rightarrow\:{z}=\sqrt[{\mathrm{3}}]{\mathrm{11}}\vee{z}=−\sqrt[{\mathrm{3}}]{\mathrm{11}}\left(\frac{\mathrm{1}}{\mathrm{2}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{i}\right)\vee{z}=−\sqrt[{\mathrm{3}}]{\mathrm{11}}\left(\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{i}\right) \\ $$$$ \\ $$$$−\sqrt{{x}};\:\sqrt{{x}}\:\mathrm{with}\:{x}\in\mathbb{R}^{+} \:\mathrm{are}\:\mathrm{just}\:\mathrm{rational}\:\mathrm{numbers} \\ $$$$\mathrm{it}\:\mathrm{makes}\:\mathrm{no}\:\mathrm{sense}\:\mathrm{to}\:\mathrm{see}\:“\mathrm{2}−\sqrt{\mathrm{3}}''\:\mathrm{as}\:\mathrm{2}\:\mathrm{different} \\ $$$$\mathrm{numbers}…\:\mathrm{you}\:\mathrm{also}\:\mathrm{don}'\mathrm{t}\:\mathrm{see}\:“−\mathrm{3}''\:\mathrm{when} \\ $$$$“\mathrm{3}''\:\mathrm{is}\:\mathrm{written}. \\ $$
