Menu Close

Question-56525

Tinku Tara 0 Comments
Pin




Question Number 56525 by Sr@2004 last updated on 18/Mar/19
Commented by Sr@2004 last updated on 18/Mar/19
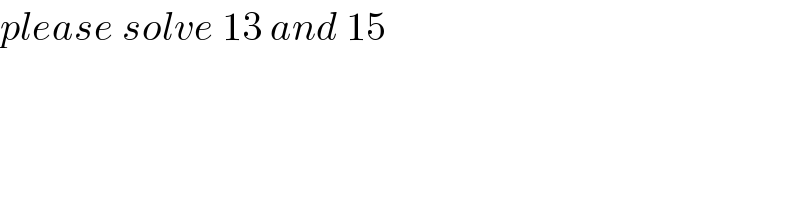
please solve 13 and 15
$${please}\:{solve}\:\mathrm{13}\:{and}\:\mathrm{15} \\ $$
Commented by Sr@2004 last updated on 18/Mar/19
sorry 13 and 14
$${sorry}\:\mathrm{13}\:{and}\:\mathrm{14} \\ $$
Answered by MJS last updated on 18/Mar/19
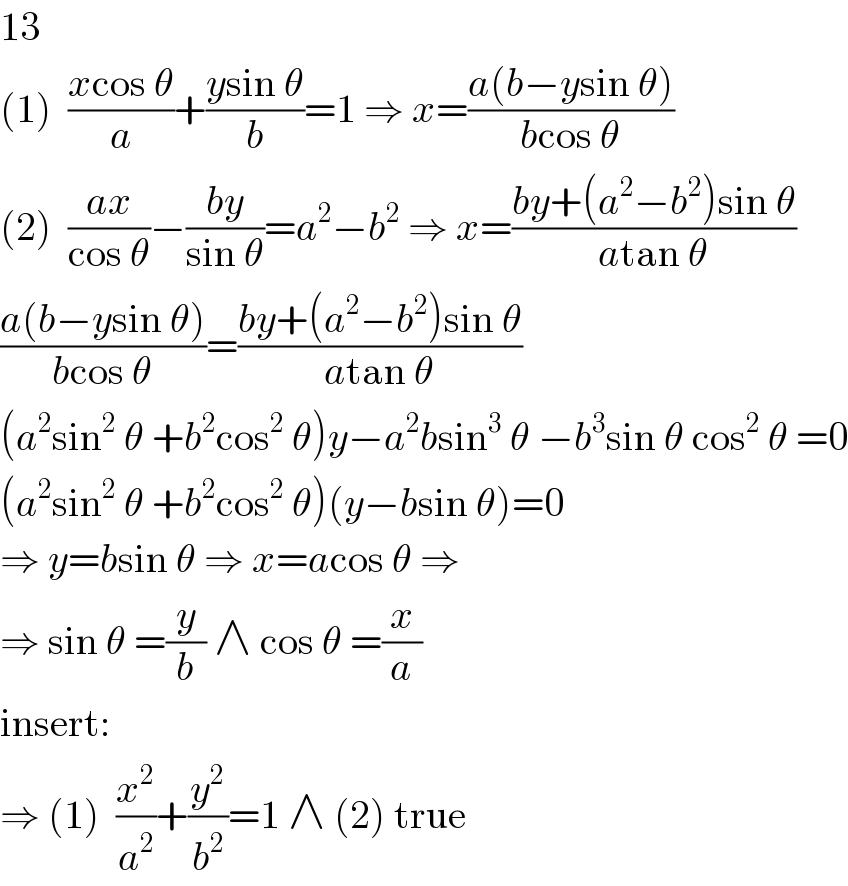
13 (1) ((xcos θ)/a)+((ysin θ)/b)=1 ⇒ x=((a(b−ysin θ))/(bcos θ)) (2) ((ax)/(cos θ))−((by)/(sin θ))=a^2 −b^2 ⇒ x=((by+(a^2 −b^2 )sin θ)/(atan θ)) ((a(b−ysin θ))/(bcos θ))=((by+(a^2 −b^2 )sin θ)/(atan θ)) (a^2 sin^2 θ +b^2 cos^2 θ)y−a^2 bsin^3 θ −b^3 sin θ cos^2 θ =0 (a^2 sin^2 θ +b^2 cos^2 θ)(y−bsin θ)=0 ⇒ y=bsin θ ⇒ x=acos θ ⇒ ⇒ sin θ =(y/b) ∧ cos θ =(x/a) insert: ⇒ (1) (x^2 /a^2 )+(y^2 /b^2 )=1 ∧ (2) true
$$\mathrm{13} \\ $$$$\left(\mathrm{1}\right)\:\:\frac{{x}\mathrm{cos}\:\theta}{{a}}+\frac{{y}\mathrm{sin}\:\theta}{{b}}=\mathrm{1}\:\Rightarrow\:{x}=\frac{{a}\left({b}−{y}\mathrm{sin}\:\theta\right)}{{b}\mathrm{cos}\:\theta} \\ $$$$\left(\mathrm{2}\right)\:\:\frac{{ax}}{\mathrm{cos}\:\theta}−\frac{{by}}{\mathrm{sin}\:\theta}={a}^{\mathrm{2}} −{b}^{\mathrm{2}} \:\Rightarrow\:{x}=\frac{{by}+\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)\mathrm{sin}\:\theta}{{a}\mathrm{tan}\:\theta} \\ $$$$\frac{{a}\left({b}−{y}\mathrm{sin}\:\theta\right)}{{b}\mathrm{cos}\:\theta}=\frac{{by}+\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)\mathrm{sin}\:\theta}{{a}\mathrm{tan}\:\theta} \\ $$$$\left({a}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\theta\:+{b}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \:\theta\right){y}−{a}^{\mathrm{2}} {b}\mathrm{sin}^{\mathrm{3}} \:\theta\:−{b}^{\mathrm{3}} \mathrm{sin}\:\theta\:\mathrm{cos}^{\mathrm{2}} \:\theta\:=\mathrm{0} \\ $$$$\left({a}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\theta\:+{b}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \:\theta\right)\left({y}−{b}\mathrm{sin}\:\theta\right)=\mathrm{0} \\ $$$$\Rightarrow\:{y}={b}\mathrm{sin}\:\theta\:\Rightarrow\:{x}={a}\mathrm{cos}\:\theta\:\Rightarrow \\ $$$$\Rightarrow\:\mathrm{sin}\:\theta\:=\frac{{y}}{{b}}\:\wedge\:\mathrm{cos}\:\theta\:=\frac{{x}}{{a}} \\ $$$$\mathrm{insert}: \\ $$$$\Rightarrow\:\left(\mathrm{1}\right)\:\:\frac{{x}^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{{y}^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\mathrm{1}\:\wedge\:\left(\mathrm{2}\right)\:\mathrm{true} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 18/Mar/19
13)((xcosθ)/a)+((ysinθ)/b)=1 xp+yq=1 ×(1/q) [p=((cosθ)/a) q=((sinθ)/b)] (x/p)−(y/q)=a^2 −b^2 ×q ((xp)/q)+y=(1/q) ((xq)/p)−y=q(a^2 −b^2 ) x(((p^2 +q^2 )/(pq)))=q(a^2 −b^2 )+(1/q) x=((q^2 (a^2 −b^2 )+1)/q)×((pq)/((p^2 +q^2 ))) x=((cosθ)/a)×(1/((((cosθ)/a))^2 +(((sinθ)/b))^2 ))×[(((sinθ)/b))^2 (a^2 −b^2 )+1] x=((cosθ)/a)×((a^2 b^2 )/(b^2 cos^2 θ+a^2 sin^2 θ))×[((b^2 +a^2 sin^2 θ−b^2 sin^2 θ)/b^2 )] (x/a)=cosθ×(1/(b^2 cos^2 θ+a^2 sin^2 θ))×[a^2 sin^2 θ+b^2 cos^2 θ] (x/a)=cosθ ((xcosθ)/a)+((ysinθ)/b)=1 ((ysinθ)/b)=1−cos^2 θ (y/b)=sinθ ((x/a))^2 +((y/b))^2 cos^2 θ+sin^2 θ =1 proved
$$\left.\mathrm{13}\right)\frac{{xcos}\theta}{{a}}+\frac{{ysin}\theta}{{b}}=\mathrm{1} \\ $$$${xp}+{yq}=\mathrm{1}\:×\frac{\mathrm{1}}{{q}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left[{p}=\frac{{cos}\theta}{{a}}\:\:\:\:{q}=\frac{{sin}\theta}{{b}}\right] \\ $$$$\frac{{x}}{{p}}−\frac{{y}}{{q}}={a}^{\mathrm{2}} −{b}^{\mathrm{2}} \:\:\:\:\:×{q} \\ $$$$\frac{{xp}}{{q}}+{y}=\frac{\mathrm{1}}{{q}} \\ $$$$\frac{{xq}}{{p}}−{y}={q}\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right) \\ $$$${x}\left(\frac{{p}^{\mathrm{2}} +{q}^{\mathrm{2}} }{{pq}}\right)={q}\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)+\frac{\mathrm{1}}{{q}} \\ $$$${x}=\frac{{q}^{\mathrm{2}} \left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)+\mathrm{1}}{{q}}×\frac{{pq}}{\left({p}^{\mathrm{2}} +{q}^{\mathrm{2}} \right)} \\ $$$${x}=\frac{{cos}\theta}{{a}}×\frac{\mathrm{1}}{\left(\frac{{cos}\theta}{{a}}\right)^{\mathrm{2}} +\left(\frac{{sin}\theta}{{b}}\right)^{\mathrm{2}} }×\left[\left(\frac{{sin}\theta}{{b}}\right)^{\mathrm{2}} \left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)+\mathrm{1}\right] \\ $$$${x}=\frac{{cos}\theta}{{a}}×\frac{{a}^{\mathrm{2}} {b}^{\mathrm{2}} }{{b}^{\mathrm{2}} {cos}^{\mathrm{2}} \theta+{a}^{\mathrm{2}} {sin}^{\mathrm{2}} \theta}×\left[\frac{{b}^{\mathrm{2}} +{a}^{\mathrm{2}} {sin}^{\mathrm{2}} \theta−{b}^{\mathrm{2}} {sin}^{\mathrm{2}} \theta}{{b}^{\mathrm{2}} }\right] \\ $$$$\frac{{x}}{{a}}={cos}\theta×\frac{\mathrm{1}}{{b}^{\mathrm{2}} {cos}^{\mathrm{2}} \theta+{a}^{\mathrm{2}} {sin}^{\mathrm{2}} \theta}×\left[{a}^{\mathrm{2}} {sin}^{\mathrm{2}} \theta+{b}^{\mathrm{2}} {cos}^{\mathrm{2}} \theta\right] \\ $$$$\frac{{x}}{{a}}={cos}\theta \\ $$$$\frac{{xcos}\theta}{{a}}+\frac{{ysin}\theta}{{b}}=\mathrm{1} \\ $$$$\frac{{ysin}\theta}{{b}}=\mathrm{1}−{cos}^{\mathrm{2}} \theta \\ $$$$\frac{{y}}{{b}}={sin}\theta \\ $$$$\left(\frac{{x}}{{a}}\right)^{\mathrm{2}} +\left(\frac{{y}}{{b}}\right)^{\mathrm{2}} \\ $$$${cos}^{\mathrm{2}} \theta+{sin}^{\mathrm{2}} \theta \\ $$$$=\mathrm{1}\:{proved} \\ $$
Commented by Sr@2004 last updated on 18/Mar/19
I cannot understand it.
$${I}\:{cannot}\:{understand}\:{it}. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 18/Mar/19
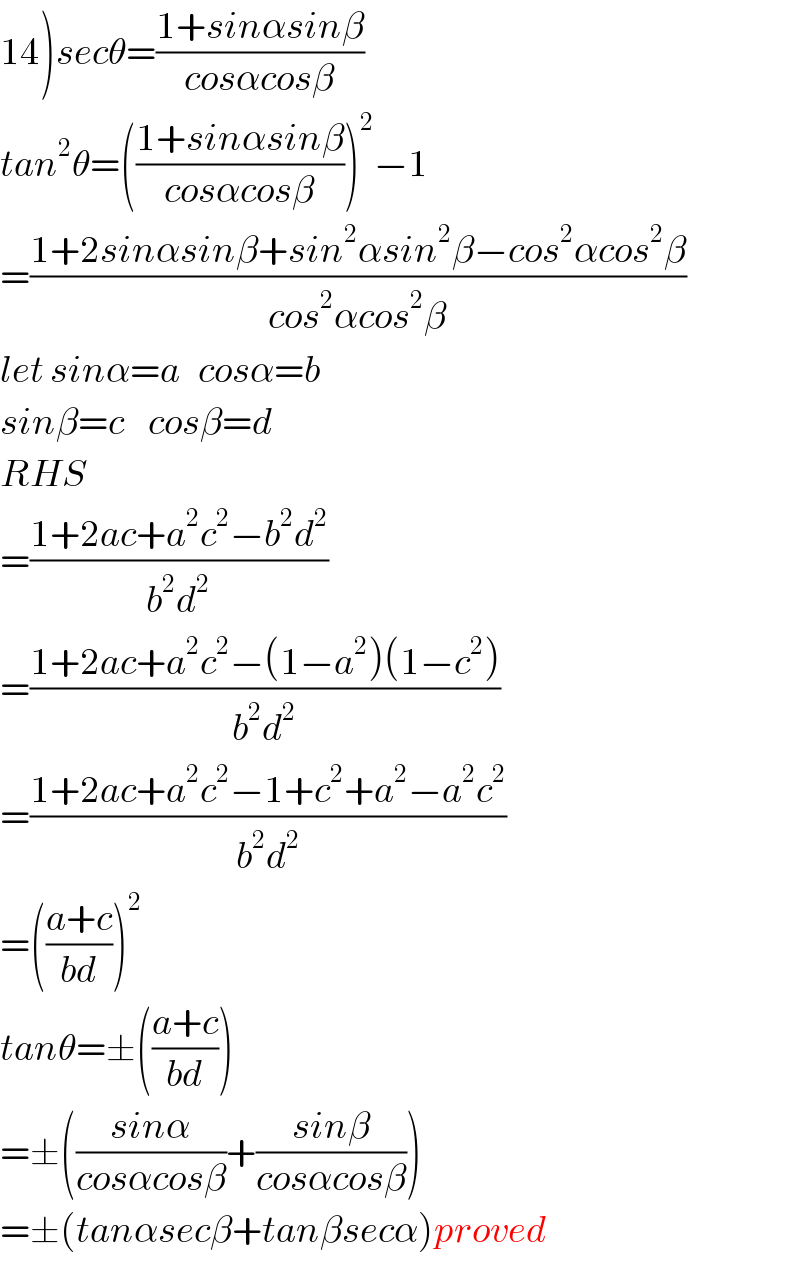
14)secθ=((1+sinαsinβ)/(cosαcosβ)) tan^2 θ=(((1+sinαsinβ)/(cosαcosβ)))^2 −1 =((1+2sinαsinβ+sin^2 αsin^2 β−cos^2 αcos^2 β)/(cos^2 αcos^2 β)) let sinα=a cosα=b sinβ=c cosβ=d RHS =((1+2ac+a^2 c^2 −b^2 d^2 )/(b^2 d^2 )) =((1+2ac+a^2 c^2 −(1−a^2 )(1−c^2 ))/(b^2 d^2 )) =((1+2ac+a^2 c^2 −1+c^2 +a^2 −a^2 c^2 )/(b^2 d^2 )) =(((a+c)/(bd)))^2 tanθ=±(((a+c)/(bd))) =±(((sinα)/(cosαcosβ))+((sinβ)/(cosαcosβ))) =±(tanαsecβ+tanβsecα)proved
$$\left.\mathrm{14}\right){sec}\theta=\frac{\mathrm{1}+{sin}\alpha{sin}\beta}{{cos}\alpha{cos}\beta} \\ $$$${tan}^{\mathrm{2}} \theta=\left(\frac{\mathrm{1}+{sin}\alpha{sin}\beta}{{cos}\alpha{cos}\beta}\right)^{\mathrm{2}} −\mathrm{1} \\ $$$$=\frac{\mathrm{1}+\mathrm{2}{sin}\alpha{sin}\beta+{sin}^{\mathrm{2}} \alpha{sin}^{\mathrm{2}} \beta−{cos}^{\mathrm{2}} \alpha{cos}^{\mathrm{2}} \beta}{{cos}^{\mathrm{2}} \alpha{cos}^{\mathrm{2}} \beta} \\ $$$${let}\:{sin}\alpha={a}\:\:\:{cos}\alpha={b} \\ $$$${sin}\beta={c}\:\:\:\:{cos}\beta={d} \\ $$$${RHS} \\ $$$$=\frac{\mathrm{1}+\mathrm{2}{ac}+{a}^{\mathrm{2}} {c}^{\mathrm{2}} −{b}^{\mathrm{2}} {d}^{\mathrm{2}} }{{b}^{\mathrm{2}} {d}^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}+\mathrm{2}{ac}+{a}^{\mathrm{2}} {c}^{\mathrm{2}} −\left(\mathrm{1}−{a}^{\mathrm{2}} \right)\left(\mathrm{1}−{c}^{\mathrm{2}} \right)}{{b}^{\mathrm{2}} {d}^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}+\mathrm{2}{ac}+{a}^{\mathrm{2}} {c}^{\mathrm{2}} −\mathrm{1}+{c}^{\mathrm{2}} +{a}^{\mathrm{2}} −{a}^{\mathrm{2}} {c}^{\mathrm{2}} }{{b}^{\mathrm{2}} {d}^{\mathrm{2}} } \\ $$$$=\left(\frac{{a}+{c}}{{bd}}\right)^{\mathrm{2}} \\ $$$${tan}\theta=\pm\left(\frac{{a}+{c}}{{bd}}\right) \\ $$$$=\pm\left(\frac{{sin}\alpha}{{cos}\alpha{cos}\beta}+\frac{{sin}\beta}{{cos}\alpha{cos}\beta}\right) \\ $$$$=\pm\left({tan}\alpha{sec}\beta+{tan}\beta{sec}\alpha\right){proved} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 19/Mar/19
13)let ((xcosθ)/a)+((ysinθ)/b)=1 bxcosθ+aysinθ=ab x(bcosθ)+y(asinθ)=ab....(1) ((ax)/(cosθ))−((by)/(sinθ))=a^2 −b^2 x(asinθ)+y(−bcosθ)=(a^2 −b^2 )sinθcosθ.×asinθ x(bcosθ)+y(asinθ)=ab×bcosθ x(a^2 sin^2 θ+b^2 cos^2 θ)=a(a^2 −b^2 )sin^2 θcosθ+ab^2 cosθ x(a^2 sin^2 θ+b^2 cos^2 θ)=acosθ[a^2 sin^2 θ−b^2 sin^2 θ+b^2 ] x(a^2 sin^2 θ+b^2 cos^2 θ)=acosθ[a^2 sin^2 θ+b^2 cos^2 θ] x=acosθ ((xcosθ)/a)+((ysinθ)/b)=1 cos^2 θ+((ysinθ)/b)=sin^2 θ+cos^2 θ ((ysinθ)/b)=sin^2 θ y=bsinθ so ((x/a))^2 +((y/b))^2 cos^2 θ+sin^2 θ=1 proved (/)
$$\left.\mathrm{13}\right){let}\:\frac{{xcos}\theta}{{a}}+\frac{{ysin}\theta}{{b}}=\mathrm{1} \\ $$$${bxcos}\theta+{aysin}\theta={ab} \\ $$$${x}\left({bcos}\theta\right)+{y}\left({asin}\theta\right)={ab}….\left(\mathrm{1}\right) \\ $$$$\frac{{ax}}{{cos}\theta}−\frac{{by}}{{sin}\theta}={a}^{\mathrm{2}} −{b}^{\mathrm{2}} \\ $$$${x}\left({asin}\theta\right)+{y}\left(−{bcos}\theta\right)=\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right){sin}\theta{cos}\theta.×{asin}\theta \\ $$$${x}\left({bcos}\theta\right)+{y}\left({asin}\theta\right)={ab}×{bcos}\theta \\ $$$$ \\ $$$${x}\left({a}^{\mathrm{2}} {sin}^{\mathrm{2}} \theta+{b}^{\mathrm{2}} {cos}^{\mathrm{2}} \theta\right)={a}\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right){sin}^{\mathrm{2}} \theta{cos}\theta+{ab}^{\mathrm{2}} {cos}\theta \\ $$$${x}\left({a}^{\mathrm{2}} {sin}^{\mathrm{2}} \theta+{b}^{\mathrm{2}} {cos}^{\mathrm{2}} \theta\right)={acos}\theta\left[{a}^{\mathrm{2}} {sin}^{\mathrm{2}} \theta−{b}^{\mathrm{2}} {sin}^{\mathrm{2}} \theta+{b}^{\mathrm{2}} \right] \\ $$$${x}\left({a}^{\mathrm{2}} {sin}^{\mathrm{2}} \theta+{b}^{\mathrm{2}} {cos}^{\mathrm{2}} \theta\right)={acos}\theta\left[{a}^{\mathrm{2}} {sin}^{\mathrm{2}} \theta+{b}^{\mathrm{2}} {cos}^{\mathrm{2}} \theta\right] \\ $$$${x}={acos}\theta \\ $$$$\frac{{xcos}\theta}{{a}}+\frac{{ysin}\theta}{{b}}=\mathrm{1} \\ $$$${cos}^{\mathrm{2}} \theta+\frac{{ysin}\theta}{{b}}={sin}^{\mathrm{2}} \theta+{cos}^{\mathrm{2}} \theta \\ $$$$\frac{{ysin}\theta}{{b}}={sin}^{\mathrm{2}} \theta \\ $$$${y}={bsin}\theta \\ $$$${so} \\ $$$$\left(\frac{{x}}{{a}}\right)^{\mathrm{2}} +\left(\frac{{y}}{{b}}\right)^{\mathrm{2}} \\ $$$${cos}^{\mathrm{2}} \theta+{sin}^{\mathrm{2}} \theta=\mathrm{1}\:{proved} \\ $$$$\frac{}{} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *