Question Number 56540 by Gulay last updated on 18/Mar/19

Commented by Gulay last updated on 18/Mar/19
$$\mathrm{sir}\:\mathrm{plz}\:\mathrm{plz}\:\mathrm{help}\:\mathrm{me} \\ $$
Answered by MJS last updated on 18/Mar/19
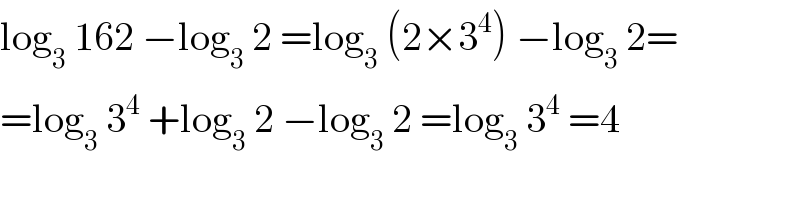
$$\mathrm{log}_{\mathrm{3}} \:\mathrm{162}\:−\mathrm{log}_{\mathrm{3}} \:\mathrm{2}\:=\mathrm{log}_{\mathrm{3}} \:\left(\mathrm{2}×\mathrm{3}^{\mathrm{4}} \right)\:−\mathrm{log}_{\mathrm{3}} \:\mathrm{2}= \\ $$$$=\mathrm{log}_{\mathrm{3}} \:\mathrm{3}^{\mathrm{4}} \:+\mathrm{log}_{\mathrm{3}} \:\mathrm{2}\:−\mathrm{log}_{\mathrm{3}} \:\mathrm{2}\:=\mathrm{log}_{\mathrm{3}} \:\mathrm{3}^{\mathrm{4}} \:=\mathrm{4} \\ $$
Commented by Gulay last updated on 18/Mar/19

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{so}\:\mathrm{much}\:\mathrm{sir}\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you} \\ $$
Answered by MJS last updated on 18/Mar/19
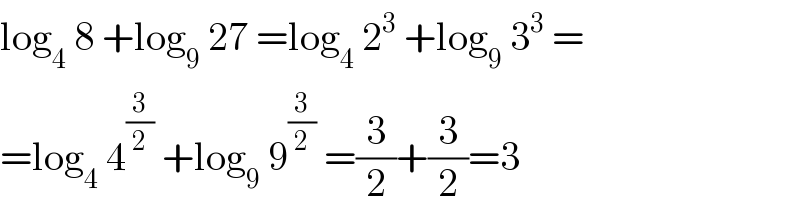
$$\mathrm{log}_{\mathrm{4}} \:\mathrm{8}\:+\mathrm{log}_{\mathrm{9}} \:\mathrm{27}\:=\mathrm{log}_{\mathrm{4}} \:\mathrm{2}^{\mathrm{3}} \:+\mathrm{log}_{\mathrm{9}} \:\mathrm{3}^{\mathrm{3}} \:= \\ $$$$=\mathrm{log}_{\mathrm{4}} \:\mathrm{4}^{\frac{\mathrm{3}}{\mathrm{2}}} \:+\mathrm{log}_{\mathrm{9}} \:\mathrm{9}^{\frac{\mathrm{3}}{\mathrm{2}}} \:=\frac{\mathrm{3}}{\mathrm{2}}+\frac{\mathrm{3}}{\mathrm{2}}=\mathrm{3} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 18/Mar/19
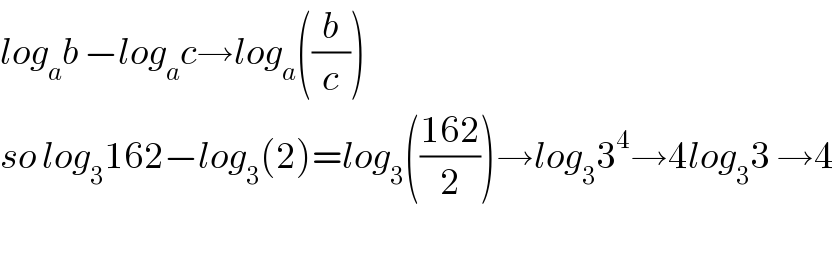
$${log}_{{a}} {b}\:−{log}_{{a}} {c}\rightarrow{log}_{{a}} \left(\frac{{b}}{{c}}\right) \\ $$$${so}\:{log}_{\mathrm{3}} \mathrm{162}−{log}_{\mathrm{3}} \left(\mathrm{2}\right)={log}_{\mathrm{3}} \left(\frac{\mathrm{162}}{\mathrm{2}}\right)\rightarrow{log}_{\mathrm{3}} \mathrm{3}^{\mathrm{4}} \rightarrow\mathrm{4}{log}_{\mathrm{3}} \mathrm{3}\:\rightarrow\mathrm{4} \\ $$$$ \\ $$
Answered by MJS last updated on 18/Mar/19
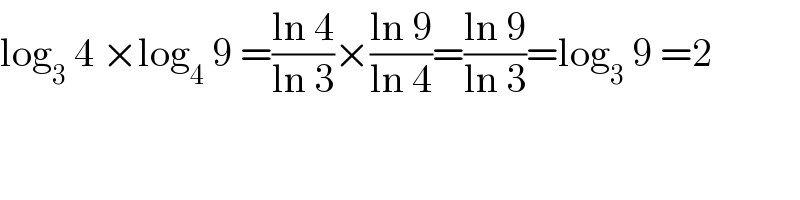
$$\mathrm{log}_{\mathrm{3}} \:\mathrm{4}\:×\mathrm{log}_{\mathrm{4}} \:\mathrm{9}\:=\frac{\mathrm{ln}\:\mathrm{4}}{\mathrm{ln}\:\mathrm{3}}×\frac{\mathrm{ln}\:\mathrm{9}}{\mathrm{ln}\:\mathrm{4}}=\frac{\mathrm{ln}\:\mathrm{9}}{\mathrm{ln}\:\mathrm{3}}=\mathrm{log}_{\mathrm{3}} \:\mathrm{9}\:=\mathrm{2} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 18/Mar/19
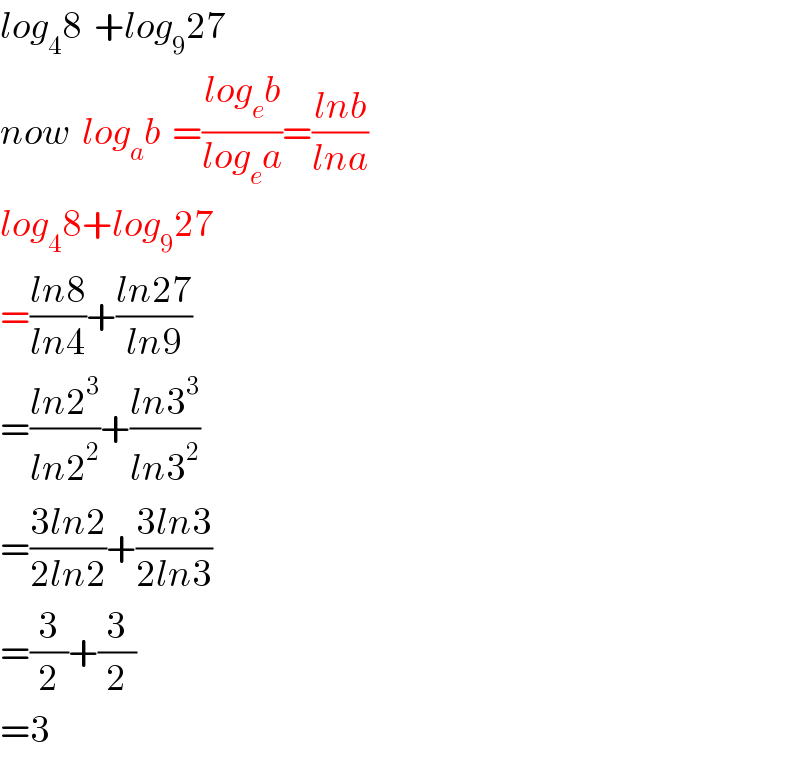
$${log}_{\mathrm{4}} \mathrm{8}\:\:+{log}_{\mathrm{9}} \mathrm{27} \\ $$$${now}\:\:{log}_{{a}} {b}\:\:=\frac{{log}_{{e}} {b}}{{log}_{{e}} {a}}=\frac{{lnb}}{{lna}} \\ $$$${log}_{\mathrm{4}} \mathrm{8}+{log}_{\mathrm{9}} \mathrm{27} \\ $$$$=\frac{{ln}\mathrm{8}}{{ln}\mathrm{4}}+\frac{{ln}\mathrm{27}}{{ln}\mathrm{9}} \\ $$$$=\frac{{ln}\mathrm{2}^{\mathrm{3}} }{{ln}\mathrm{2}^{\mathrm{2}} }+\frac{{ln}\mathrm{3}^{\mathrm{3}} }{{ln}\mathrm{3}^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{3}{ln}\mathrm{2}}{\mathrm{2}{ln}\mathrm{2}}+\frac{\mathrm{3}{ln}\mathrm{3}}{\mathrm{2}{ln}\mathrm{3}} \\ $$$$=\frac{\mathrm{3}}{\mathrm{2}}+\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$=\mathrm{3} \\ $$
