Question Number 56575 by Sr@2004 last updated on 18/Mar/19

Commented by Sr@2004 last updated on 18/Mar/19
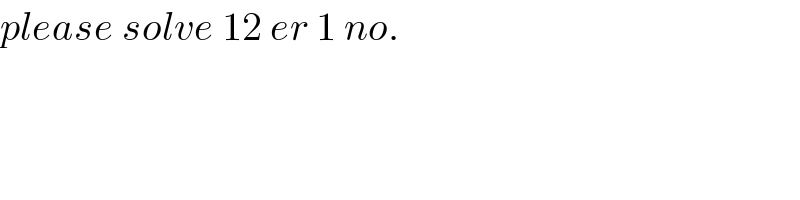
$${please}\:{solve}\:\mathrm{12}\:{er}\:\mathrm{1}\:{no}. \\ $$
Commented by Sr@2004 last updated on 20/Mar/19

Answered by tanmay.chaudhury50@gmail.com last updated on 18/Mar/19
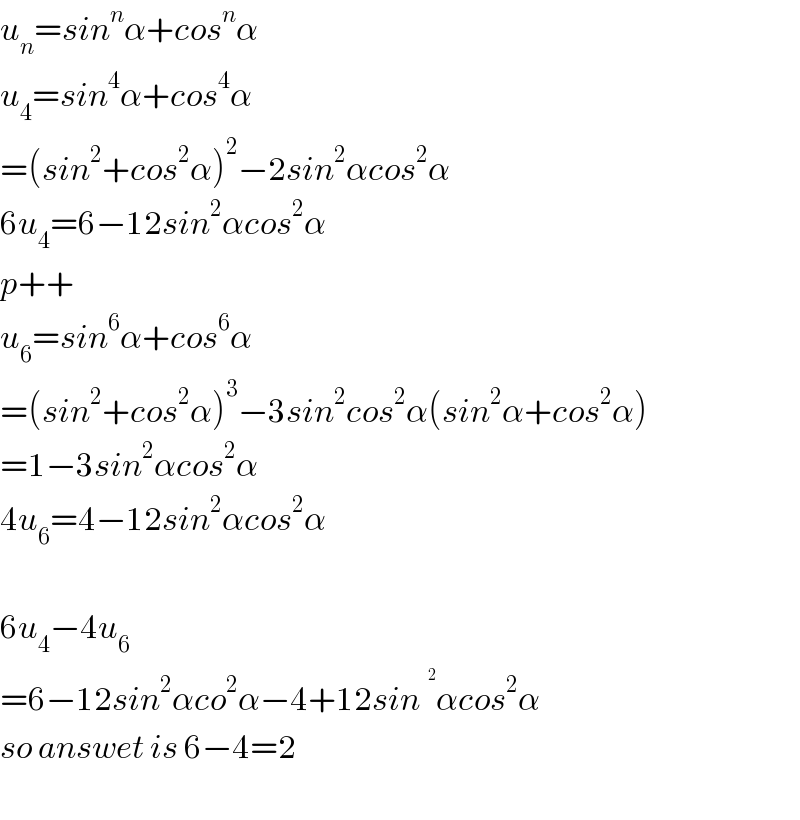
$${u}_{{n}} ={sin}^{{n}} \alpha+{cos}^{{n}} \alpha \\ $$$${u}_{\mathrm{4}} ={sin}^{\mathrm{4}} \alpha+{cos}^{\mathrm{4}} \alpha \\ $$$$=\left({sin}^{\mathrm{2}} +{cos}^{\mathrm{2}} \alpha\right)^{\mathrm{2}} −\mathrm{2}{sin}^{\mathrm{2}} \alpha{cos}^{\mathrm{2}} \alpha \\ $$$$\mathrm{6}{u}_{\mathrm{4}} =\mathrm{6}−\mathrm{12}{sin}^{\mathrm{2}} \alpha{cos}^{\mathrm{2}} \alpha \\ $$$${p}++ \\ $$$${u}_{\mathrm{6}} ={sin}^{\mathrm{6}} \alpha+{cos}^{\mathrm{6}} \alpha \\ $$$$=\left({sin}^{\mathrm{2}} +{cos}^{\mathrm{2}} \alpha\right)^{\mathrm{3}} −\mathrm{3}{sin}^{\mathrm{2}} {cos}^{\mathrm{2}} \alpha\left({sin}^{\mathrm{2}} \alpha+{cos}^{\mathrm{2}} \alpha\right) \\ $$$$=\mathrm{1}−\mathrm{3}{sin}^{\mathrm{2}} \alpha{cos}^{\mathrm{2}} \alpha \\ $$$$\mathrm{4}{u}_{\mathrm{6}} =\mathrm{4}−\mathrm{12}{sin}^{\mathrm{2}} \alpha{cos}^{\mathrm{2}} \alpha \\ $$$$ \\ $$$$\mathrm{6}{u}_{\mathrm{4}} −\mathrm{4}{u}_{\mathrm{6}} \\ $$$$=\mathrm{6}−\mathrm{12}{sin}^{\mathrm{2}} \alpha{co}^{\mathrm{2}} \alpha−\mathrm{4}+\mathrm{12}{sin}^{} \alpha{cos}^{\mathrm{2}} \alpha \\ $$$${so}\:{answet}\:{is}\:\mathrm{6}−\mathrm{4}=\mathrm{2} \\ $$$$ \\ $$
