Question Number 56597 by Tawa1 last updated on 19/Mar/19

Commented by Tawa1 last updated on 19/Mar/19

$$\mathrm{Please}\:\mathrm{help}\:\mathrm{me}\:\mathrm{prove}\:\mathrm{the}\:\mathrm{sum}\:\mathrm{of}\:\mathrm{an}\:\mathrm{arithmetico}\:−\:\mathrm{geometric}\:\mathrm{series}, \\ $$$$\mathrm{and}\:\mathrm{the}\:\mathrm{sum}\:\mathrm{to}\:\mathrm{infinity}.\:\:\: \\ $$$$\boldsymbol{\mathrm{Again}} \\ $$$$\:\:\:\:\mathrm{How}\:\mathrm{does}\:\mathrm{the}\:\mathrm{3x}\:\mathrm{in}\:\mathrm{the}\:\mathrm{above}\:\mathrm{solution}\:\mathrm{disappear}. \\ $$$$\mathrm{From}\:\:\:\:\:\:\:\mathrm{3x}\:+\:\left(\mathrm{2x}^{\mathrm{2}} \:+\:\mathrm{2x}^{\mathrm{3}} \:+\:…\:+\:\mathrm{2x}^{\mathrm{n}} \right)\:−\:\left(\mathrm{2n}\:+\:\mathrm{1}\right)\mathrm{x}^{\mathrm{n}\:+\:\mathrm{1}} \:\: \\ $$$$\mathrm{to}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{x}\:+\:\left(\mathrm{2x}\:+\:\mathrm{2x}^{\mathrm{2}} \:+\:\mathrm{2x}^{\mathrm{3}} \:+\:…\:+\:\mathrm{2x}^{\mathrm{n}} \right)\:−\:\left(\mathrm{2n}\:+\:\mathrm{1}\right)\mathrm{x}^{\mathrm{n}\:+\:\mathrm{1}} \:\: \\ $$$$\mathrm{in}\:\mathrm{next}\:\mathrm{line}\:… \\ $$$$ \\ $$$$\mathrm{Thanks}. \\ $$
Commented by Kunal12588 last updated on 19/Mar/19
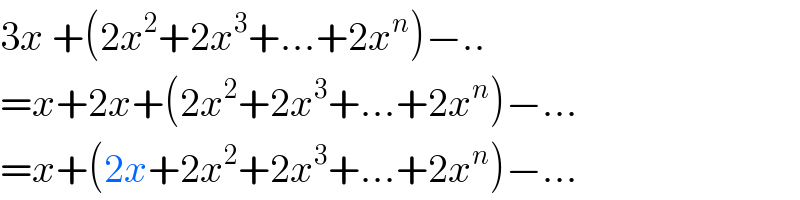
$$\mathrm{3}{x}\:+\left(\mathrm{2}{x}^{\mathrm{2}} +\mathrm{2}{x}^{\mathrm{3}} +…+\mathrm{2}{x}^{{n}} \right)−.. \\ $$$$={x}+\mathrm{2}{x}+\left(\mathrm{2}{x}^{\mathrm{2}} +\mathrm{2}{x}^{\mathrm{3}} +…+\mathrm{2}{x}^{{n}} \right)−… \\ $$$$={x}+\left(\mathrm{2}{x}+\mathrm{2}{x}^{\mathrm{2}} +\mathrm{2}{x}^{\mathrm{3}} +…+\mathrm{2}{x}^{{n}} \right)−… \\ $$
Commented by Tawa1 last updated on 19/Mar/19
$$\mathrm{Ohh}.\:\mathrm{I}\:\mathrm{understand}\:\mathrm{now}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}\:… \\ $$
