Menu Close

Question-56777

Tinku Tara 0 Comments
Pin




Question Number 56777 by ajfour last updated on 23/Mar/19
Commented by ajfour last updated on 23/Mar/19
Find x and T.
$$\mathrm{Find}\:\mathrm{x}\:\mathrm{and}\:\mathrm{T}. \\ $$
Answered by mr W last updated on 23/Mar/19
Commented by mr W last updated on 24/Mar/19
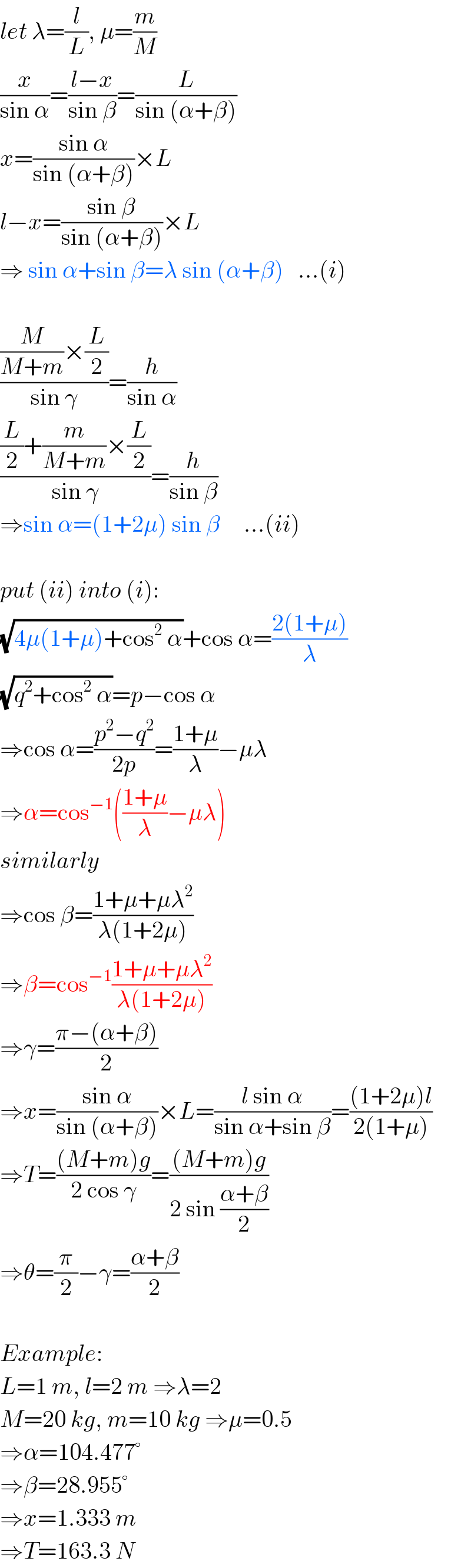
let λ=(l/L), μ=(m/M) (x/(sin α))=((l−x)/(sin β))=(L/(sin (α+β))) x=((sin α)/(sin (α+β)))×L l−x=((sin β)/(sin (α+β)))×L ⇒ sin α+sin β=λ sin (α+β) ...(i) (((M/(M+m))×(L/2))/(sin γ))=(h/(sin α)) (((L/2)+(m/(M+m))×(L/2))/(sin γ))=(h/(sin β)) ⇒sin α=(1+2μ) sin β ...(ii) put (ii) into (i): (√(4μ(1+μ)+cos^2 α))+cos α=((2(1+μ))/λ) (√(q^2 +cos^2 α))=p−cos α ⇒cos α=((p^2 −q^2 )/(2p))=((1+μ)/λ)−μλ ⇒α=cos^(−1) (((1+μ)/λ)−μλ) similarly ⇒cos β=((1+μ+μλ^2 )/(λ(1+2μ))) ⇒β=cos^(−1) ((1+μ+μλ^2 )/(λ(1+2μ))) ⇒γ=((π−(α+β))/2) ⇒x=((sin α)/(sin (α+β)))×L=((l sin α)/(sin α+sin β))=(((1+2μ)l)/(2(1+μ))) ⇒T=(((M+m)g)/(2 cos γ))=(((M+m)g)/(2 sin ((α+β)/2))) ⇒θ=(π/2)−γ=((α+β)/2) Example: L=1 m, l=2 m ⇒λ=2 M=20 kg, m=10 kg ⇒μ=0.5 ⇒α=104.477° ⇒β=28.955° ⇒x=1.333 m ⇒T=163.3 N
$${let}\:\lambda=\frac{{l}}{{L}},\:\mu=\frac{{m}}{{M}} \\ $$$$\frac{{x}}{\mathrm{sin}\:\alpha}=\frac{{l}−{x}}{\mathrm{sin}\:\beta}=\frac{{L}}{\mathrm{sin}\:\left(\alpha+\beta\right)} \\ $$$${x}=\frac{\mathrm{sin}\:\alpha}{\mathrm{sin}\:\left(\alpha+\beta\right)}×{L} \\ $$$${l}−{x}=\frac{\mathrm{sin}\:\beta}{\mathrm{sin}\:\left(\alpha+\beta\right)}×{L} \\ $$$$\Rightarrow\:\mathrm{sin}\:\alpha+\mathrm{sin}\:\beta=\lambda\:\mathrm{sin}\:\left(\alpha+\beta\right)\:\:\:…\left({i}\right) \\ $$$$ \\ $$$$\frac{\frac{{M}}{{M}+{m}}×\frac{{L}}{\mathrm{2}}}{\mathrm{sin}\:\gamma}=\frac{{h}}{\mathrm{sin}\:\alpha} \\ $$$$\frac{\frac{{L}}{\mathrm{2}}+\frac{{m}}{{M}+{m}}×\frac{{L}}{\mathrm{2}}}{\mathrm{sin}\:\gamma}=\frac{{h}}{\mathrm{sin}\:\beta} \\ $$$$\Rightarrow\mathrm{sin}\:\alpha=\left(\mathrm{1}+\mathrm{2}\mu\right)\:\mathrm{sin}\:\beta\:\:\:\:\:…\left({ii}\right) \\ $$$$ \\ $$$${put}\:\left({ii}\right)\:{into}\:\left({i}\right): \\ $$$$\sqrt{\mathrm{4}\mu\left(\mathrm{1}+\mu\right)+\mathrm{cos}^{\mathrm{2}} \:\alpha}+\mathrm{cos}\:\alpha=\frac{\mathrm{2}\left(\mathrm{1}+\mu\right)}{\lambda} \\ $$$$\sqrt{{q}^{\mathrm{2}} +\mathrm{cos}^{\mathrm{2}} \:\alpha}={p}−\mathrm{cos}\:\alpha \\ $$$$\Rightarrow\mathrm{cos}\:\alpha=\frac{{p}^{\mathrm{2}} −{q}^{\mathrm{2}} }{\mathrm{2}{p}}=\frac{\mathrm{1}+\mu}{\lambda}−\mu\lambda \\ $$$$\Rightarrow\alpha=\mathrm{cos}^{−\mathrm{1}} \left(\frac{\mathrm{1}+\mu}{\lambda}−\mu\lambda\right) \\ $$$${similarly} \\ $$$$\Rightarrow\mathrm{cos}\:\beta=\frac{\mathrm{1}+\mu+\mu\lambda^{\mathrm{2}} }{\lambda\left(\mathrm{1}+\mathrm{2}\mu\right)} \\ $$$$\Rightarrow\beta=\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{1}+\mu+\mu\lambda^{\mathrm{2}} }{\lambda\left(\mathrm{1}+\mathrm{2}\mu\right)} \\ $$$$\Rightarrow\gamma=\frac{\pi−\left(\alpha+\beta\right)}{\mathrm{2}} \\ $$$$\Rightarrow{x}=\frac{\mathrm{sin}\:\alpha}{\mathrm{sin}\:\left(\alpha+\beta\right)}×{L}=\frac{{l}\:\mathrm{sin}\:\alpha}{\mathrm{sin}\:\alpha+\mathrm{sin}\:\beta}=\frac{\left(\mathrm{1}+\mathrm{2}\mu\right){l}}{\mathrm{2}\left(\mathrm{1}+\mu\right)} \\ $$$$\Rightarrow{T}=\frac{\left({M}+{m}\right){g}}{\mathrm{2}\:\mathrm{cos}\:\gamma}=\frac{\left({M}+{m}\right){g}}{\mathrm{2}\:\mathrm{sin}\:\frac{\alpha+\beta}{\mathrm{2}}} \\ $$$$\Rightarrow\theta=\frac{\pi}{\mathrm{2}}−\gamma=\frac{\alpha+\beta}{\mathrm{2}} \\ $$$$ \\ $$$${Example}: \\ $$$${L}=\mathrm{1}\:{m},\:{l}=\mathrm{2}\:{m}\:\Rightarrow\lambda=\mathrm{2} \\ $$$${M}=\mathrm{20}\:{kg},\:{m}=\mathrm{10}\:{kg}\:\Rightarrow\mu=\mathrm{0}.\mathrm{5} \\ $$$$\Rightarrow\alpha=\mathrm{104}.\mathrm{477}° \\ $$$$\Rightarrow\beta=\mathrm{28}.\mathrm{955}° \\ $$$$\Rightarrow{x}=\mathrm{1}.\mathrm{333}\:{m} \\ $$$$\Rightarrow{T}=\mathrm{163}.\mathrm{3}\:{N} \\ $$
Commented by ajfour last updated on 23/Mar/19
thank you Sir.
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{Sir}. \\ $$
Commented by mr W last updated on 23/Mar/19
it should look like this when the system is in equilibrium.
$${it}\:{should}\:{look}\:{like}\:{this}\:{when}\:{the}\:{system} \\ $$$${is}\:{in}\:{equilibrium}. \\ $$
Commented by mr W last updated on 24/Mar/19
Commented by mr W last updated on 24/Mar/19
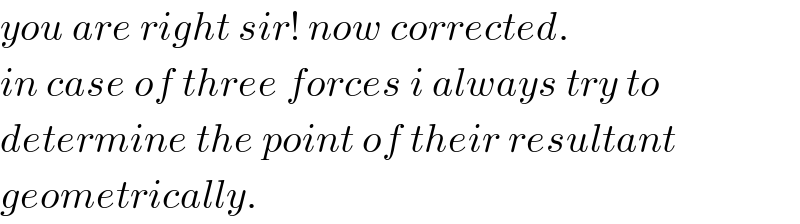
you are right sir! now corrected. in case of three forces i always try to determine the point of their resultant geometrically.
$${you}\:{are}\:{right}\:{sir}!\:{now}\:{corrected}. \\ $$$${in}\:{case}\:{of}\:{three}\:{forces}\:{i}\:{always}\:{try}\:{to} \\ $$$${determine}\:{the}\:{point}\:{of}\:{their}\:{resultant} \\ $$$${geometrically}. \\ $$
Commented by ajfour last updated on 24/Mar/19
Torque about right end of rod, TLsin β=((MgLcos θ)/2) ⇒ T=((Mgcos θ)/(2sin β)) ...(i) Tcos (β−θ)=Tcos (α+θ) ⇒ β−θ = α+θ ....(iia) ⇒ θ=((α+β)/2) .....(iib) xcos (β−θ)+(l−x)cos (α+θ)=Lcos θ ....(iii) (l−x)sin (α+θ)=xsin (β−θ)+Lsin θ .....(iv) From Torque about pulley point, (((L/2)cos θ−(l−x)cos (α+θ))/((l−x)cos (α+θ))) =(m/M) ⇒ ((Lcos θ)/(2(l−x)cos (α+θ)))=((m+M)/M) ...(v) from (iii), (iv) using (iia) lcos (α+θ)=Lcos θ ...(1) (l−2x)sin (α+θ)=Lsin θ ...(2) Now (v) implies (l/(2(l−x)))=((m+M)/M) ⇒ Ml = 2(m+M)(l−x) ____________________________ ⇒ x=(1+(m/(M+m)))(l/2) ____________________________ from (1) &(2) (((Lcos θ)/l))^2 +(((Lsin θ)/(l−2x)))^2 = 1 ⇒ ((cos^2 θ)/l^2 )+(((M+m)^2 sin^2 θ)/(m^2 l^2 )) = (1/L^2 ) ⇒ cos^2 θ[(((M+m)/m))^2 −1]=(((M+m)/m))^2 −(l^2 /L^2 ) ⇒ cos^2 θ = (((((M+m)/m))^2 −((l/L))^2 )/((((M+m)/M))^2 −1)) sin β =sin (β−θ+θ) =sin (α+θ+θ) =(((Lsin θ)/(l−2x)))cos θ+(((Lcos θ)/l))sin θ =(Lsin θcos θ)((1/l)−((M+m)/(ml))) =−((MLsin θcos θ)/(ml)) And as T=((Mgcos θ)/(2sin β)) ...(i) ⇒ T = −((mgl)/(2Lsin θ)) (θ<0) ____________________________ T= ((mgl)/(2L(√(1−(((((M+m)/m))^2 −((l/L))^2 )/((((M+m)/m))^2 −1)))))) & x=(1+(m/(M+m)))(l/2) ____________________________.
$$\mathrm{Torque}\:\mathrm{about}\:\mathrm{right}\:\mathrm{end}\:\mathrm{of}\:\mathrm{rod}, \\ $$$$\mathrm{TLsin}\:\beta=\frac{\mathrm{MgLcos}\:\theta}{\mathrm{2}} \\ $$$$\Rightarrow\:\:\mathrm{T}=\frac{\mathrm{Mgcos}\:\theta}{\mathrm{2sin}\:\beta}\:\:\:\:\:…\left(\mathrm{i}\right) \\ $$$$\:\mathrm{Tcos}\:\left(\beta−\theta\right)=\mathrm{Tcos}\:\left(\alpha+\theta\right) \\ $$$$\Rightarrow\:\:\beta−\theta\:=\:\alpha+\theta\:\:\:….\left(\mathrm{iia}\right) \\ $$$$\Rightarrow\:\:\theta=\frac{\alpha+\beta}{\mathrm{2}}\:\:\:\:\:\:\:\:\:\:\:\:…..\left(\mathrm{iib}\right) \\ $$$$\:\:\mathrm{xcos}\:\left(\beta−\theta\right)+\left({l}−\mathrm{x}\right)\mathrm{cos}\:\left(\alpha+\theta\right)=\mathrm{Lcos}\:\theta \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:….\left(\mathrm{iii}\right) \\ $$$$\:\:\left({l}−\mathrm{x}\right)\mathrm{sin}\:\left(\alpha+\theta\right)=\mathrm{xsin}\:\left(\beta−\theta\right)+\mathrm{Lsin}\:\theta \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:…..\left(\mathrm{iv}\right) \\ $$$$\:\:\mathrm{From}\:\mathrm{Torque}\:\mathrm{about}\:\mathrm{pulley}\:\mathrm{point}, \\ $$$$\:\:\:\:\:\frac{\frac{\mathrm{L}}{\mathrm{2}}\mathrm{cos}\:\theta−\left({l}−\mathrm{x}\right)\mathrm{cos}\:\left(\alpha+\theta\right)}{\left({l}−\mathrm{x}\right)\mathrm{cos}\:\left(\alpha+\theta\right)}\:=\frac{\mathrm{m}}{\mathrm{M}}\: \\ $$$$\Rightarrow\:\:\frac{\mathrm{Lcos}\:\theta}{\mathrm{2}\left({l}−\mathrm{x}\right)\mathrm{cos}\:\left(\alpha+\theta\right)}=\frac{\mathrm{m}+\mathrm{M}}{\mathrm{M}}\:\:\:\:…\left(\mathrm{v}\right) \\ $$$$\:\:\mathrm{from}\:\left(\mathrm{iii}\right),\:\left(\mathrm{iv}\right)\:\:\mathrm{using}\:\left(\mathrm{iia}\right) \\ $$$$\:\:\:{l}\mathrm{cos}\:\left(\alpha+\theta\right)=\mathrm{Lcos}\:\theta\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:…\left(\mathrm{1}\right) \\ $$$$\:\:\:\left({l}−\mathrm{2x}\right)\mathrm{sin}\:\left(\alpha+\theta\right)=\mathrm{Lsin}\:\theta\:\:\:\:\:\:…\left(\mathrm{2}\right) \\ $$$$\mathrm{Now}\:\left(\mathrm{v}\right)\:\mathrm{implies} \\ $$$$\:\:\:\:\:\:\frac{{l}}{\mathrm{2}\left({l}−\mathrm{x}\right)}=\frac{\mathrm{m}+\mathrm{M}}{\mathrm{M}} \\ $$$$\Rightarrow\:\:\:\mathrm{M}{l}\:=\:\mathrm{2}\left(\mathrm{m}+\mathrm{M}\right)\left({l}−\mathrm{x}\right) \\ $$$$\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \\ $$$$\Rightarrow\:\:\:\:\mathrm{x}=\left(\mathrm{1}+\frac{\mathrm{m}}{\mathrm{M}+\mathrm{m}}\right)\frac{{l}}{\mathrm{2}} \\ $$$$\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \\ $$$$\mathrm{from}\:\left(\mathrm{1}\right)\:\&\left(\mathrm{2}\right) \\ $$$$\:\:\left(\frac{\mathrm{Lcos}\:\theta}{{l}}\right)^{\mathrm{2}} +\left(\frac{\mathrm{Lsin}\:\theta}{{l}−\mathrm{2x}}\right)^{\mathrm{2}} =\:\mathrm{1} \\ $$$$\Rightarrow\:\:\frac{\mathrm{cos}\:^{\mathrm{2}} \theta}{{l}^{\mathrm{2}} }+\frac{\left(\mathrm{M}+\mathrm{m}\right)^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \theta}{\mathrm{m}^{\mathrm{2}} {l}^{\mathrm{2}} }\:=\:\frac{\mathrm{1}}{\mathrm{L}^{\mathrm{2}} } \\ $$$$\Rightarrow\:\mathrm{cos}\:^{\mathrm{2}} \theta\left[\left(\frac{\mathrm{M}+\mathrm{m}}{\mathrm{m}}\right)^{\mathrm{2}} −\mathrm{1}\right]=\left(\frac{\mathrm{M}+\mathrm{m}}{\mathrm{m}}\right)^{\mathrm{2}} −\frac{{l}^{\mathrm{2}} }{\mathrm{L}^{\mathrm{2}} } \\ $$$$\Rightarrow\:\:\mathrm{cos}\:^{\mathrm{2}} \theta\:=\:\frac{\left(\frac{\mathrm{M}+\mathrm{m}}{\mathrm{m}}\right)^{\mathrm{2}} −\left(\frac{{l}}{\mathrm{L}}\right)^{\mathrm{2}} }{\left(\frac{\mathrm{M}+\mathrm{m}}{\mathrm{M}}\right)^{\mathrm{2}} −\mathrm{1}} \\ $$$$\:\:\:\:\mathrm{sin}\:\beta\:=\mathrm{sin}\:\left(\beta−\theta+\theta\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{sin}\:\left(\alpha+\theta+\theta\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\left(\frac{\mathrm{Lsin}\:\theta}{{l}−\mathrm{2x}}\right)\mathrm{cos}\:\theta+\left(\frac{\mathrm{Lcos}\:\theta}{{l}}\right)\mathrm{sin}\:\theta \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\left(\mathrm{Lsin}\:\theta\mathrm{cos}\:\theta\right)\left(\frac{\mathrm{1}}{{l}}−\frac{\mathrm{M}+\mathrm{m}}{\mathrm{m}{l}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:=−\frac{\mathrm{MLsin}\:\theta\mathrm{cos}\:\theta}{\mathrm{m}{l}} \\ $$$$\:\mathrm{And}\:\mathrm{as}\:\:\:\:\mathrm{T}=\frac{\mathrm{Mgcos}\:\theta}{\mathrm{2sin}\:\beta}\:\:\:\:\:…\left(\mathrm{i}\right) \\ $$$$\Rightarrow\:\:\:\:\:\:\mathrm{T}\:=\:−\frac{\mathrm{mg}{l}}{\mathrm{2Lsin}\:\theta}\:\:\:\:\:\:\left(\theta<\mathrm{0}\right) \\ $$$$\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \\ $$$$\:\:\:\:\:\:\mathrm{T}=\:\:\frac{\mathrm{mg}{l}}{\mathrm{2L}\sqrt{\mathrm{1}−\frac{\left(\frac{\mathrm{M}+\mathrm{m}}{\mathrm{m}}\right)^{\mathrm{2}} −\left(\frac{{l}}{\mathrm{L}}\right)^{\mathrm{2}} }{\left(\frac{\mathrm{M}+\mathrm{m}}{\mathrm{m}}\right)^{\mathrm{2}} −\mathrm{1}}}} \\ $$$$\&\:\:\:\:\:\:\mathrm{x}=\left(\mathrm{1}+\frac{\mathrm{m}}{\mathrm{M}+\mathrm{m}}\right)\frac{{l}}{\mathrm{2}}\: \\ $$$$\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *