Question Number 56900 by bshahid010@gmail.com last updated on 26/Mar/19
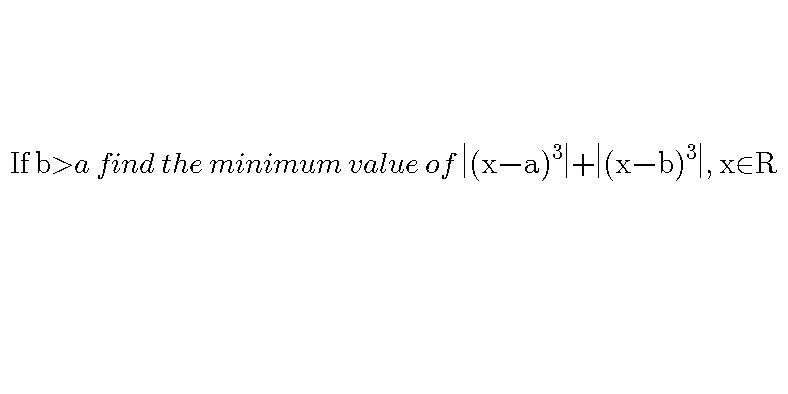
Answered by tanmay.chaudhury50@gmail.com last updated on 26/Mar/19
![f(x)=∣(x−a)^3 ∣+∣(x−b)^3 ∣ =(x−a)^3 +(x−b)^3 when x>b =(b−a)^3 when x=b =(x−a)^3 −(x−b)^3 when b>x>a =−(a−b)^3 when x=a =(b−a)^3 =−(x−a)^3 −(x−b)^3 when x<a when x>b f(x)=(x−a)^3 +(x−b)^3 (df/dx)=3(x−a)^2 +3(x−b)^2 (df/dx)≠0 as x>b but for max/min (df/dx)=0 (d^2 f/dx^2 )=6(x−a)+6(x−b) so no max/min value at x>b when b>x>a f(x)=(x−a)^3 −(x−b)^3 (df/dx)=3(x−a)^2 −3(x−b)^2 (df/dx)=0 at x=((a+b)/2) (d^2 f/dx^2 )=6(x−a)−6(x−b)=6(b−a)>0 so at x=((a+b)/2) i,e f(((a+b)/2))=minimum f(((a+b)/2))=(((a+b)/2)−a)^3 −(((a+b)/2)−b)^3 =(((b−a)/2))^3 −(((a−b)/2))^3 =2×(((b−a)/2))^3 ←this is the answer (minimum value) when x<a f(x)=−(x−a)^3 −(x−b)^3 (df/dx)=−3[(x−a)^2 +(x−b)^2 ] but (df/dx)≠0 so no min/max when x<a](https://www.tinkutara.com/question/Q56903.png)
$${f}\left({x}\right)=\mid\left({x}−{a}\right)^{\mathrm{3}} \mid+\mid\left({x}−{b}\right)^{\mathrm{3}} \mid \\ $$$$\:\:\:\:\:\:\:\:\:\:=\left({x}−{a}\right)^{\mathrm{3}} +\left({x}−{b}\right)^{\mathrm{3}} \:\:\:\:\:{when}\:{x}>{b} \\ $$$$\:\:\:\:\:\:\:\:\:\:=\left({b}−{a}\right)^{\mathrm{3}} \:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{when}\:{x}={b} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\left({x}−{a}\right)^{\mathrm{3}} −\left({x}−{b}\right)^{\mathrm{3}} \:\:\:\:\:\:\:{when}\:{b}>{x}>{a} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=−\left({a}−{b}\right)^{\mathrm{3}} \:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{when}\:{x}={a} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\left({b}−{a}\right)^{\mathrm{3}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:=−\left({x}−{a}\right)^{\mathrm{3}} −\left({x}−{b}\right)^{\mathrm{3}} \:\:{when}\:{x}<{a} \\ $$$$ \\ $$$${when}\:{x}>{b} \\ $$$${f}\left({x}\right)=\left({x}−{a}\right)^{\mathrm{3}} +\left({x}−{b}\right)^{\mathrm{3}} \\ $$$$\frac{{df}}{{dx}}=\mathrm{3}\left({x}−{a}\right)^{\mathrm{2}} +\mathrm{3}\left({x}−{b}\right)^{\mathrm{2}} \\ $$$$\frac{{df}}{{dx}}\neq\mathrm{0}\:\:\:\:{as}\:{x}>{b} \\ $$$${but}\:{for}\:{max}/{min}\:\frac{{df}}{{dx}}=\mathrm{0} \\ $$$$\frac{{d}^{\mathrm{2}} {f}}{{dx}^{\mathrm{2}} }=\mathrm{6}\left({x}−{a}\right)+\mathrm{6}\left({x}−{b}\right) \\ $$$${so}\:{no}\:{max}/{min}\:{value}\:{at}\:{x}>{b} \\ $$$$ \\ $$$${when}\:{b}>{x}>{a} \\ $$$${f}\left({x}\right)=\left({x}−{a}\right)^{\mathrm{3}} −\left({x}−{b}\right)^{\mathrm{3}} \\ $$$$\frac{{df}}{{dx}}=\mathrm{3}\left({x}−{a}\right)^{\mathrm{2}} −\mathrm{3}\left({x}−{b}\right)^{\mathrm{2}} \\ $$$$\frac{{df}}{{dx}}=\mathrm{0}\:\:{at}\:{x}=\frac{{a}+{b}}{\mathrm{2}} \\ $$$$\frac{{d}^{\mathrm{2}} {f}}{{dx}^{\mathrm{2}} }=\mathrm{6}\left({x}−{a}\right)−\mathrm{6}\left({x}−{b}\right)=\mathrm{6}\left({b}−{a}\right)>\mathrm{0} \\ $$$${so}\:{at}\:{x}=\frac{{a}+{b}}{\mathrm{2}}\:{i},{e}\:{f}\left(\frac{{a}+{b}}{\mathrm{2}}\right)={minimum} \\ $$$${f}\left(\frac{{a}+{b}}{\mathrm{2}}\right)=\left(\frac{{a}+{b}}{\mathrm{2}}−{a}\right)^{\mathrm{3}} −\left(\frac{{a}+{b}}{\mathrm{2}}−{b}\right)^{\mathrm{3}} \\ $$$$=\left(\frac{{b}−{a}}{\mathrm{2}}\right)^{\mathrm{3}} −\left(\frac{{a}−{b}}{\mathrm{2}}\right)^{\mathrm{3}} \\ $$$$=\mathrm{2}×\left(\frac{{b}−{a}}{\mathrm{2}}\right)^{\mathrm{3}} \leftarrow{this}\:{is}\:{the}\:{answer}\:\left({minimum}\:{value}\right) \\ $$$${when}\:{x}<{a} \\ $$$${f}\left({x}\right)=−\left({x}−{a}\right)^{\mathrm{3}} −\left({x}−{b}\right)^{\mathrm{3}} \\ $$$$\frac{{df}}{{dx}}=−\mathrm{3}\left[\left({x}−{a}\right)^{\mathrm{2}} +\left({x}−{b}\right)^{\mathrm{2}} \right] \\ $$$${but}\:\frac{{df}}{{dx}}\neq\mathrm{0}\:\: \\ $$$${so}\:{no}\:{min}/{max}\:{when}\:{x}<{a} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
