Question Number 56986 by mr W last updated on 27/Mar/19

Commented by mr W last updated on 27/Mar/19

$${Find}\:{x}=? \\ $$
Answered by MJS last updated on 28/Mar/19

Commented by mr W last updated on 28/Mar/19
$${correct},\:{thank}\:{you}\:{sir}! \\ $$
Answered by mr W last updated on 28/Mar/19
Commented by mr W last updated on 28/Mar/19
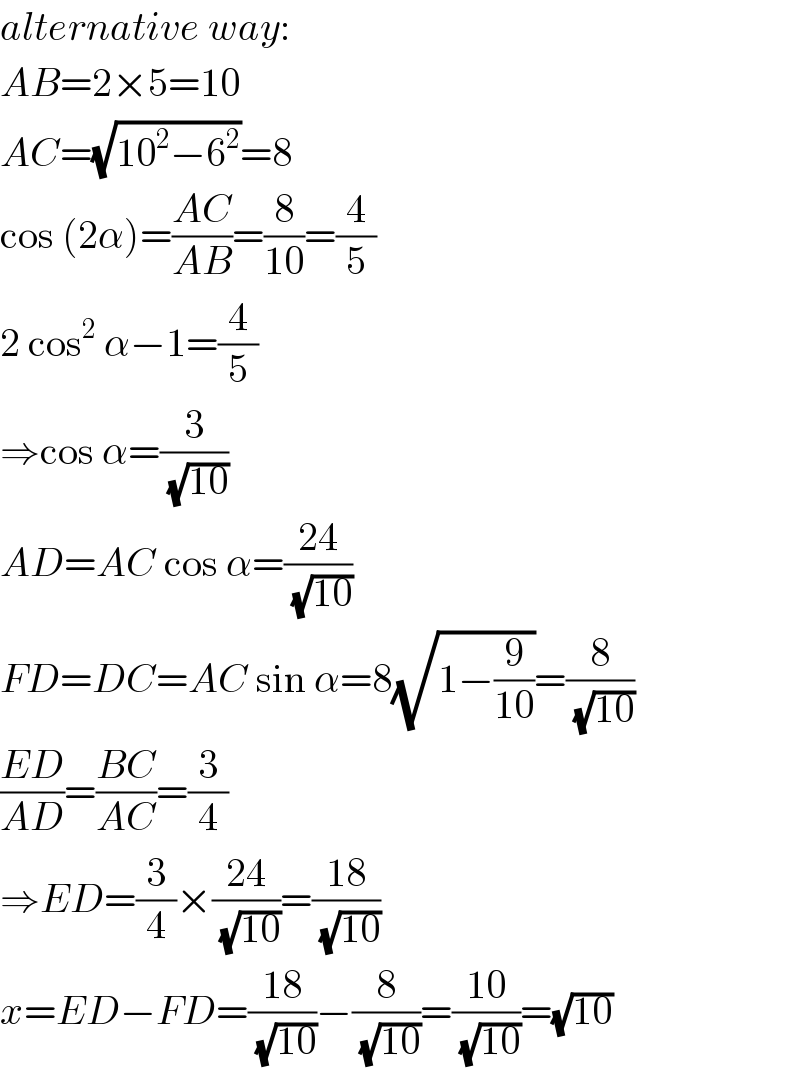
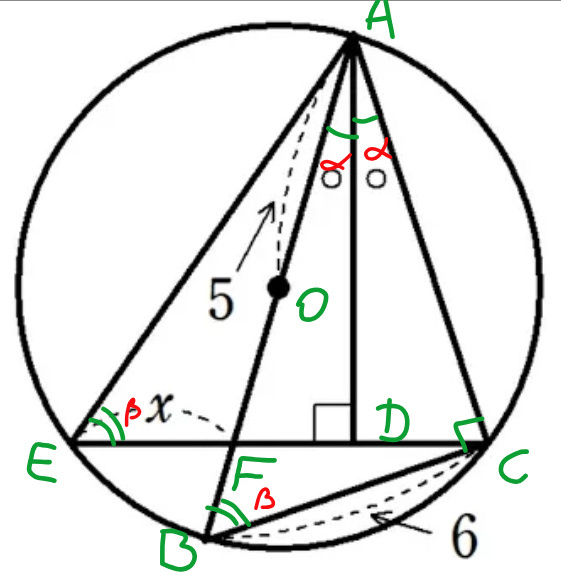
$${alternative}\:{way}: \\ $$$${AB}=\mathrm{2}×\mathrm{5}=\mathrm{10} \\ $$$${AC}=\sqrt{\mathrm{10}^{\mathrm{2}} −\mathrm{6}^{\mathrm{2}} }=\mathrm{8} \\ $$$$\mathrm{cos}\:\left(\mathrm{2}\alpha\right)=\frac{{AC}}{{AB}}=\frac{\mathrm{8}}{\mathrm{10}}=\frac{\mathrm{4}}{\mathrm{5}} \\ $$$$\mathrm{2}\:\mathrm{cos}^{\mathrm{2}} \:\alpha−\mathrm{1}=\frac{\mathrm{4}}{\mathrm{5}} \\ $$$$\Rightarrow\mathrm{cos}\:\alpha=\frac{\mathrm{3}}{\:\sqrt{\mathrm{10}}} \\ $$$${AD}={AC}\:\mathrm{cos}\:\alpha=\frac{\mathrm{24}}{\:\sqrt{\mathrm{10}}} \\ $$$${FD}={DC}={AC}\:\mathrm{sin}\:\alpha=\mathrm{8}\sqrt{\mathrm{1}−\frac{\mathrm{9}}{\mathrm{10}}}=\frac{\mathrm{8}}{\:\sqrt{\mathrm{10}}} \\ $$$$\frac{{ED}}{{AD}}=\frac{{BC}}{{AC}}=\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$\Rightarrow{ED}=\frac{\mathrm{3}}{\mathrm{4}}×\frac{\mathrm{24}}{\:\sqrt{\mathrm{10}}}=\frac{\mathrm{18}}{\:\sqrt{\mathrm{10}}} \\ $$$${x}={ED}−{FD}=\frac{\mathrm{18}}{\:\sqrt{\mathrm{10}}}−\frac{\mathrm{8}}{\:\sqrt{\mathrm{10}}}=\frac{\mathrm{10}}{\:\sqrt{\mathrm{10}}}=\sqrt{\mathrm{10}} \\ $$
