Menu Close

Question-57042

Tinku Tara 0 Comments
Pin




Question Number 57042 by mr W last updated on 29/Mar/19
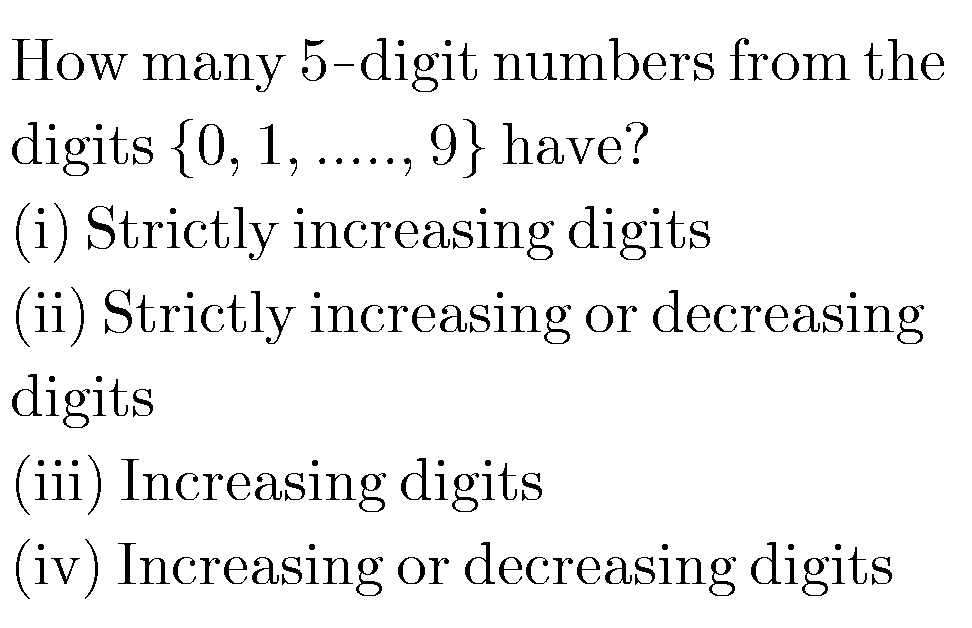
Commented by mr W last updated on 29/Mar/19
reposted Question from Tinkutara sir i found these unsolved questions in early postes and repost them.
$${reposted} \\ $$$${Question}\:{from}\:{Tinkutara}\:{sir} \\ $$$$ \\ $$$${i}\:{found}\:{these}\:{unsolved}\:{questions}\:{in} \\ $$$${early}\:{postes}\:{and}\:\:{repost}\:{them}. \\ $$
Answered by mr W last updated on 31/Mar/19
(i) number with strictly increasing digits is e.g. 13478. when five digits from {1,2,...,9} are selected, they can always form a number with 5 strictly increasing digits. therefore the answer is C_5 ^9 =126 or we can selectet at most one from each digit from 1 to 9. the answer is the coef. of term x^5 from (1+x)^9 , which is C_5 ^9 . (iii) number with increasing digits is e.g. 12236 or 12222. that means we can select at most 4 from each digit from 1 to 9. the answer is the coef. of term x^5 from (1+x+x^2 +x^3 +x^4 )^9 . (1+x+x^2 +x^3 +x^4 )^9 =(((1−x^5 )^9 )/((1−x)^9 )) =Σ_(k=0) ^9 C_k ^9 (−1)^k x^(5k) Σ_(k=0) ^∞ C_k ^(8+k) x^k term of x^5 is: C_1 ^9 (−1)^1 x^5 C_0 ^8 x^0 +C_0 ^9 (−1)^0 x^0 C_5 ^(13) x^5 =(−C_1 ^9 C_0 ^8 +C_0 ^9 C_5 ^(13) )x^5 =(−C_1 ^9 +C_5 ^(13) )x^5 =(−9+1287)x^5 =1278x^5 ⇒answer is 1278.
$$\left({i}\right) \\ $$$${number}\:{with}\:{strictly}\:{increasing}\:{digits}\: \\ $$$${is}\:{e}.{g}.\:\mathrm{13478}. \\ $$$${when}\:{five}\:{digits}\:{from}\:\left\{\mathrm{1},\mathrm{2},…,\mathrm{9}\right\}\:{are} \\ $$$${selected},\:{they}\:{can}\:{always}\:{form}\:{a} \\ $$$${number}\:{with}\:\mathrm{5}\:{strictly}\:{increasing} \\ $$$${digits}. \\ $$$${therefore}\:{the}\:{answer}\:{is} \\ $$$${C}_{\mathrm{5}} ^{\mathrm{9}} =\mathrm{126} \\ $$$${or}\:{we}\:{can}\:{selectet}\:{at}\:{most}\:{one}\:{from} \\ $$$${each}\:{digit}\:{from}\:\mathrm{1}\:{to}\:\mathrm{9}. \\ $$$${the}\:{answer}\:{is}\:{the}\:{coef}.\:{of}\:{term}\:{x}^{\mathrm{5}} \\ $$$${from}\:\left(\mathrm{1}+{x}\right)^{\mathrm{9}} ,\:{which}\:{is}\:{C}_{\mathrm{5}} ^{\mathrm{9}} . \\ $$$$ \\ $$$$\left({iii}\right) \\ $$$${number}\:{with}\:{increasing}\:{digits}\:{is}\:{e}.{g}. \\ $$$$\mathrm{12236}\:{or}\:\mathrm{12222}. \\ $$$${that}\:{means}\:{we}\:{can}\:{select}\:{at}\:{most}\:\mathrm{4} \\ $$$${from}\:{each}\:{digit}\:{from}\:\mathrm{1}\:{to}\:\mathrm{9}. \\ $$$${the}\:{answer}\:{is}\:{the}\:{coef}.\:{of}\:{term}\:{x}^{\mathrm{5}} \\ $$$${from}\:\left(\mathrm{1}+{x}+{x}^{\mathrm{2}} +{x}^{\mathrm{3}} +{x}^{\mathrm{4}} \right)^{\mathrm{9}} . \\ $$$$\left(\mathrm{1}+{x}+{x}^{\mathrm{2}} +{x}^{\mathrm{3}} +{x}^{\mathrm{4}} \right)^{\mathrm{9}} =\frac{\left(\mathrm{1}−{x}^{\mathrm{5}} \right)^{\mathrm{9}} }{\left(\mathrm{1}−{x}\right)^{\mathrm{9}} } \\ $$$$=\underset{{k}=\mathrm{0}} {\overset{\mathrm{9}} {\sum}}{C}_{{k}} ^{\mathrm{9}} \left(−\mathrm{1}\right)^{{k}} {x}^{\mathrm{5}{k}} \underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}{C}_{{k}} ^{\mathrm{8}+{k}} {x}^{{k}} \\ $$$${term}\:{of}\:{x}^{\mathrm{5}} \:{is}: \\ $$$${C}_{\mathrm{1}} ^{\mathrm{9}} \left(−\mathrm{1}\right)^{\mathrm{1}} {x}^{\mathrm{5}} {C}_{\mathrm{0}} ^{\mathrm{8}} {x}^{\mathrm{0}} +{C}_{\mathrm{0}} ^{\mathrm{9}} \left(−\mathrm{1}\right)^{\mathrm{0}} {x}^{\mathrm{0}} {C}_{\mathrm{5}} ^{\mathrm{13}} {x}^{\mathrm{5}} \\ $$$$=\left(−{C}_{\mathrm{1}} ^{\mathrm{9}} {C}_{\mathrm{0}} ^{\mathrm{8}} +{C}_{\mathrm{0}} ^{\mathrm{9}} {C}_{\mathrm{5}} ^{\mathrm{13}} \right){x}^{\mathrm{5}} \\ $$$$=\left(−{C}_{\mathrm{1}} ^{\mathrm{9}} +{C}_{\mathrm{5}} ^{\mathrm{13}} \right){x}^{\mathrm{5}} \\ $$$$=\left(−\mathrm{9}+\mathrm{1287}\right){x}^{\mathrm{5}} \\ $$$$=\mathrm{1278}{x}^{\mathrm{5}} \\ $$$$ \\ $$$$\Rightarrow{answer}\:{is}\:\mathrm{1278}. \\ $$
Commented by mr W last updated on 31/Mar/19
(ii) number with strictly decreasing digits is e.g. 76320. that means we can select 5 digits from 0 to 9. number of numbers with strictly decreasing digits is C_5 ^(10) =252. strictly increasing or strictly decreasing: C_5 ^9 +C_5 ^(10) =126+252=378.
$$\left({ii}\right) \\ $$$${number}\:{with}\:{strictly}\:{decreasing}\:{digits}\: \\ $$$${is}\:{e}.{g}.\:\mathrm{76320}. \\ $$$${that}\:{means}\:{we}\:{can}\:{select}\:\mathrm{5}\:{digits}\:{from} \\ $$$$\mathrm{0}\:{to}\:\mathrm{9}. \\ $$$${number}\:{of}\:{numbers}\:{with}\:{strictly} \\ $$$${decreasing}\:{digits}\:{is} \\ $$$${C}_{\mathrm{5}} ^{\mathrm{10}} =\mathrm{252}. \\ $$$$ \\ $$$${strictly}\:{increasing}\:{or}\:{strictly}\:{decreasing}: \\ $$$${C}_{\mathrm{5}} ^{\mathrm{9}} +{C}_{\mathrm{5}} ^{\mathrm{10}} =\mathrm{126}+\mathrm{252}=\mathrm{378}. \\ $$
Commented by mr W last updated on 31/Mar/19
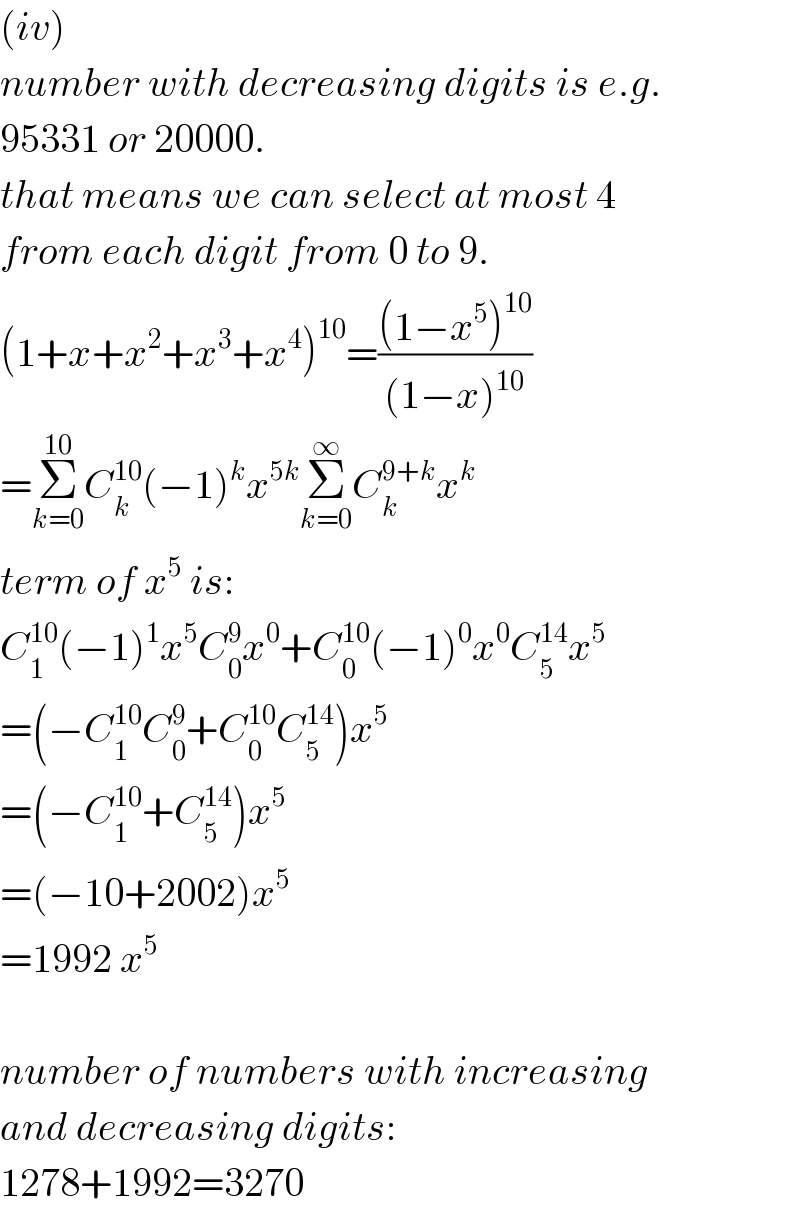
(iv) number with decreasing digits is e.g. 95331 or 20000. that means we can select at most 4 from each digit from 0 to 9. (1+x+x^2 +x^3 +x^4 )^(10) =(((1−x^5 )^(10) )/((1−x)^(10) )) =Σ_(k=0) ^(10) C_k ^(10) (−1)^k x^(5k) Σ_(k=0) ^∞ C_k ^(9+k) x^k term of x^5 is: C_1 ^(10) (−1)^1 x^5 C_0 ^9 x^0 +C_0 ^(10) (−1)^0 x^0 C_5 ^(14) x^5 =(−C_1 ^(10) C_0 ^9 +C_0 ^(10) C_5 ^(14) )x^5 =(−C_1 ^(10) +C_5 ^(14) )x^5 =(−10+2002)x^5 =1992 x^5 number of numbers with increasing and decreasing digits: 1278+1992=3270
$$\left({iv}\right) \\ $$$${number}\:{with}\:{decreasing}\:{digits}\:{is}\:{e}.{g}. \\ $$$$\mathrm{95331}\:{or}\:\mathrm{20000}. \\ $$$${that}\:{means}\:{we}\:{can}\:{select}\:{at}\:{most}\:\mathrm{4} \\ $$$${from}\:{each}\:{digit}\:{from}\:\mathrm{0}\:{to}\:\mathrm{9}. \\ $$$$\left(\mathrm{1}+{x}+{x}^{\mathrm{2}} +{x}^{\mathrm{3}} +{x}^{\mathrm{4}} \right)^{\mathrm{10}} =\frac{\left(\mathrm{1}−{x}^{\mathrm{5}} \right)^{\mathrm{10}} }{\left(\mathrm{1}−{x}\right)^{\mathrm{10}} } \\ $$$$=\underset{{k}=\mathrm{0}} {\overset{\mathrm{10}} {\sum}}{C}_{{k}} ^{\mathrm{10}} \left(−\mathrm{1}\right)^{{k}} {x}^{\mathrm{5}{k}} \underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}{C}_{{k}} ^{\mathrm{9}+{k}} {x}^{{k}} \\ $$$${term}\:{of}\:{x}^{\mathrm{5}} \:{is}: \\ $$$${C}_{\mathrm{1}} ^{\mathrm{10}} \left(−\mathrm{1}\right)^{\mathrm{1}} {x}^{\mathrm{5}} {C}_{\mathrm{0}} ^{\mathrm{9}} {x}^{\mathrm{0}} +{C}_{\mathrm{0}} ^{\mathrm{10}} \left(−\mathrm{1}\right)^{\mathrm{0}} {x}^{\mathrm{0}} {C}_{\mathrm{5}} ^{\mathrm{14}} {x}^{\mathrm{5}} \\ $$$$=\left(−{C}_{\mathrm{1}} ^{\mathrm{10}} {C}_{\mathrm{0}} ^{\mathrm{9}} +{C}_{\mathrm{0}} ^{\mathrm{10}} {C}_{\mathrm{5}} ^{\mathrm{14}} \right){x}^{\mathrm{5}} \\ $$$$=\left(−{C}_{\mathrm{1}} ^{\mathrm{10}} +{C}_{\mathrm{5}} ^{\mathrm{14}} \right){x}^{\mathrm{5}} \\ $$$$=\left(−\mathrm{10}+\mathrm{2002}\right){x}^{\mathrm{5}} \\ $$$$=\mathrm{1992}\:{x}^{\mathrm{5}} \\ $$$$ \\ $$$${number}\:{of}\:{numbers}\:{with}\:{increasing} \\ $$$${and}\:{decreasing}\:{digits}: \\ $$$$\mathrm{1278}+\mathrm{1992}=\mathrm{3270} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *