Question Number 57048 by mr W last updated on 29/Mar/19
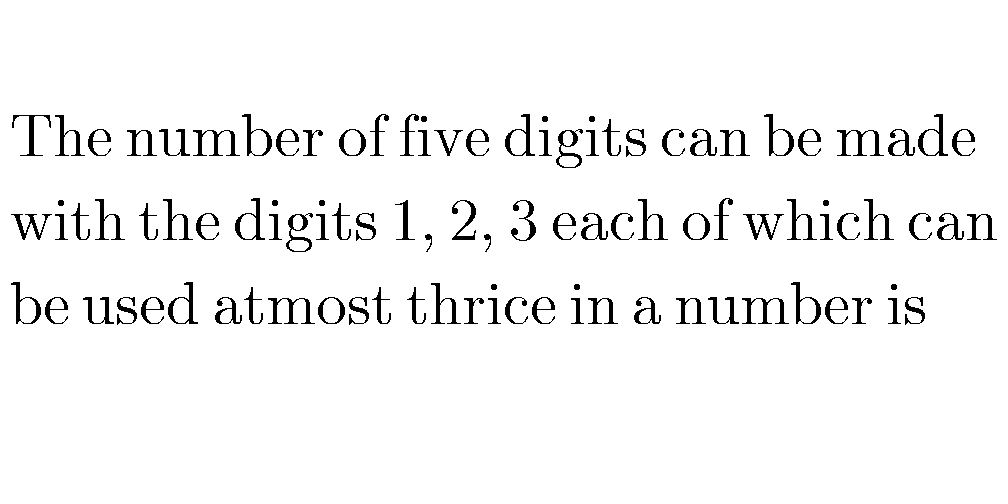
Commented by mr W last updated on 29/Mar/19
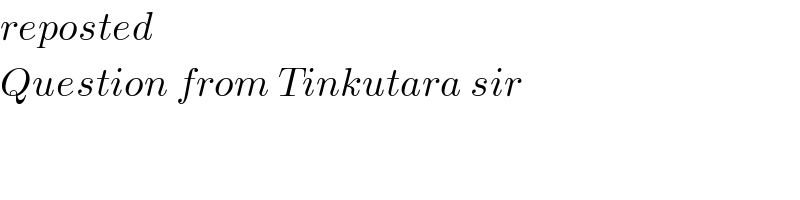
$${reposted} \\ $$$${Question}\:{from}\:{Tinkutara}\:{sir} \\ $$
Answered by mr W last updated on 29/Mar/19
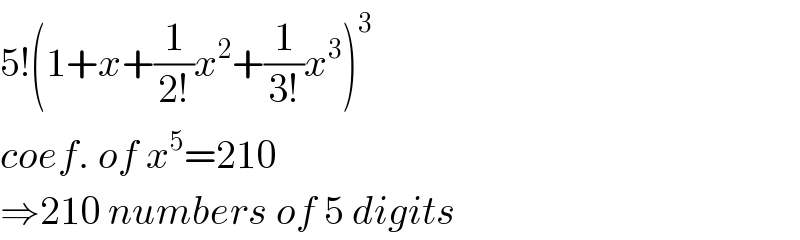
$$\mathrm{5}!\left(\mathrm{1}+{x}+\frac{\mathrm{1}}{\mathrm{2}!}{x}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{3}!}{x}^{\mathrm{3}} \right)^{\mathrm{3}} \\ $$$${coef}.\:{of}\:{x}^{\mathrm{5}} =\mathrm{210} \\ $$$$\Rightarrow\mathrm{210}\:{numbers}\:{of}\:\mathrm{5}\:{digits} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 29/Mar/19

$${use}\:{of}\:{digit}\:\mathrm{1}\:\:\:\:{use}\:{of}\:{dgt}\:\mathrm{2}\:\:\:\:\:{use}\:{of}\:{dgt}\:\mathrm{3}\: \\ $$$$\left.\:\mathrm{1}\right)\:{one}\:{time}\:\:\:\:\:\:\:\:{one}\:{times}\:\:\:\:\:\:\:{threetimes}\rightarrow\frac{\mathrm{5}!}{\mathrm{3}!}=\mathrm{20} \\ $$$$\left.\mathrm{2}\right)\:\:\:{one}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{two}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{two}\rightarrow\frac{\mathrm{5}!}{\mathrm{2}!\mathrm{2}!}=\mathrm{30} \\ $$$$\left.\mathrm{3}\right){one}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{three}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{one}\rightarrow\frac{\mathrm{5}!}{\mathrm{3}!}=\mathrm{20} \\ $$$$\left.\mathrm{4}\right){two}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{one}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{two}\rightarrow\frac{\mathrm{5}!}{\mathrm{2}!\mathrm{2}!}=\mathrm{30} \\ $$$$\left.\mathrm{5}\right){two}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{two}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{one}\rightarrow\frac{\mathrm{5}!}{\mathrm{2}!\mathrm{2}!}=\mathrm{30} \\ $$$$\left.\mathrm{6}\right){three}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{one}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{one}\rightarrow\frac{\mathrm{5}!}{\mathrm{3}!}=\mathrm{20} \\ $$$${no}\:{mention}\:{whether}\:{it}\:{is}\:{allowed}\:{non}\:{use}\:{of} \\ $$$${any}\:{digit}\:{however}\:\:{i}\:{have}\:{considered} \\ $$$$\left.\mathrm{7}\right){nil}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{tw}\mathrm{0}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{three}\rightarrow\frac{\mathrm{5}!}{\mathrm{2}!\mathrm{3}!}=\mathrm{10} \\ $$$$\left.\mathrm{8}\right){nil}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{three}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{two}\rightarrow\frac{\mathrm{5}!}{\mathrm{3}!\mathrm{2}!}=\mathrm{10} \\ $$$$\left.\mathrm{9}\right){two}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{nil}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{three}\rightarrow\frac{\mathrm{5}!}{\mathrm{2}!\mathrm{3}!}=\mathrm{10} \\ $$$$\left.\mathrm{10}\right){three}\:\:\:\:\:\:\:\:\:\:\:\:{nil}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{two}\:\rightarrow\frac{\mathrm{5}!}{\mathrm{3}!\mathrm{2}!}\:\:\:=\mathrm{10}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$$$\left.\mathrm{11}\right){two}\:\:\:\:\:\:\:\:\:\:\:\:\:\:{three}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{nil}\rightarrow\frac{\mathrm{5}!}{\mathrm{2}!\mathrm{3}!}=\mathrm{10} \\ $$$$\left.\mathrm{12}\right){three}\:\:\:\:\:\:\:\:\:\:{two}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{nil}\rightarrow\frac{\mathrm{5}!}{\mathrm{3}!\mathrm{2}!}=\mathrm{10} \\ $$$$\boldsymbol{{so}}\:\boldsymbol{{answer}}\:\boldsymbol{{is}}\:\left(\mathrm{3}×\mathrm{20}+\mathrm{3}×\mathrm{30}+\mathrm{6}×\mathrm{10}\right)=\mathrm{210} \\ $$$$ \\ $$$$\boldsymbol{{pls}}\:\boldsymbol{{check}}\:\boldsymbol{{sir}}… \\ $$$$ \\ $$
Commented by mr W last updated on 29/Mar/19
$${answer}\:{is}\:{correct}.\:{thanks}\:{sir}! \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 30/Mar/19
$${your}\:{method}\:{is}\:{tricky}\:…{i}\:{have}\:{solved}\:{on}\:{thought} \\ $$$${basis}.{Tanmay} \\ $$
Commented by mr W last updated on 30/Mar/19

$${your}\:{method}\:{is}\:{straightforward}\:{and} \\ $$$${easy}\:{to}\:{understand},\:{very}\:{good}\:{sir}! \\ $$$${we}\:{need}\:{a}\:{general}\:{method}\:{if}\:{we}\:{deal} \\ $$$${with}\:{a}\:{lot}\:{of}\:{cases},\:{e}.{g}.\:\:{when}\:{we}\:{have} \\ $$$$\mathrm{5}\:{digits}\:{to}\:{form}\:\mathrm{10}−{digit}\:{numbers}. \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 30/Mar/19

$${thank}\:{you}\:{sir}… \\ $$
