Question-57114

Question Number 57114 by Tinkutara last updated on 30/Mar/19

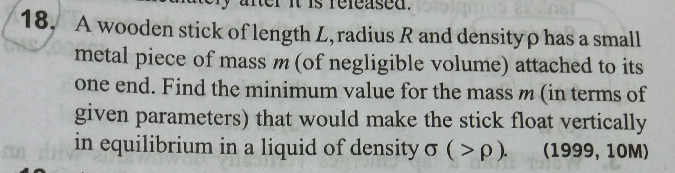
Commented by ajfour last updated on 30/Mar/19

Commented by mr W last updated on 31/Mar/19

$${nice}\:{solution}\:{sir}! \\ $$$${let}'{s}\:{say}\:{m}>{m}_{{min}} .\:{what}\:{is}\:{the}\:{periode} \\ $$$${of}\:{the}\:{swinging}\:{motion}\:{of}\:{the}\:{stick}? \\ $$

Commented by ajfour last updated on 31/Mar/19

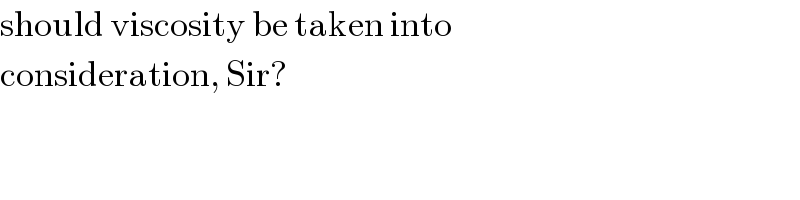
should viscosity be taken into consideration, Sir?

$$\mathrm{should}\:\mathrm{viscosity}\:\mathrm{be}\:\mathrm{taken}\:\mathrm{into} \\ $$$$\mathrm{consideration},\:\mathrm{Sir}? \\ $$

Commented by mr W last updated on 31/Mar/19

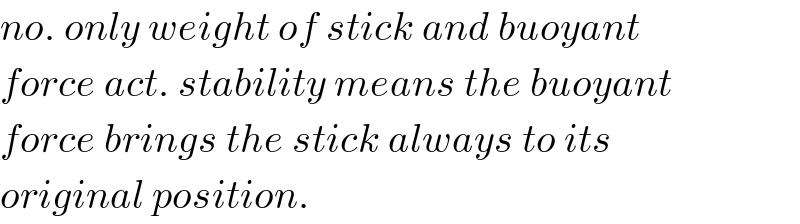
$${no}.\:{only}\:{weight}\:{of}\:{stick}\:{and}\:{buoyant} \\ $$$${force}\:{act}.\:{stability}\:{means}\:{the}\:{buoyant} \\ $$$${force}\:{brings}\:{the}\:{stick}\:{always}\:{to}\:{its} \\ $$$${original}\:{position}. \\ $$

Answered by ajfour last updated on 30/Mar/19

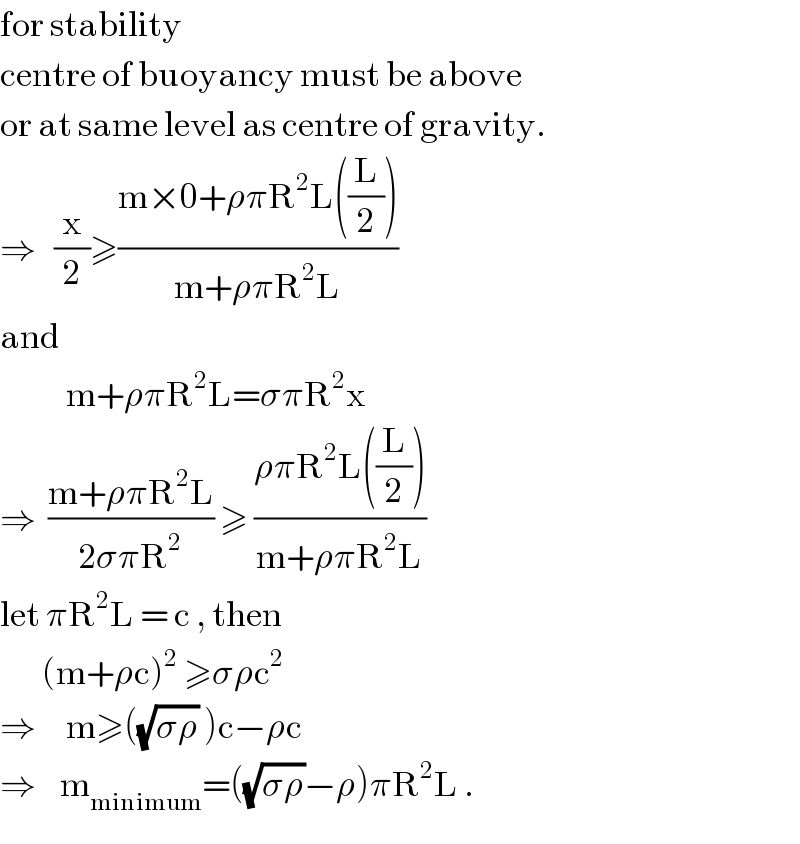
for stability centre of buoyancy must be above or at same level as centre of gravity. ⇒ (x/2)≥((m×0+ρπR^2 L((L/2)))/(m+ρπR^2 L)) and m+ρπR^2 L=σπR^2 x ⇒ ((m+ρπR^2 L)/(2σπR^2 )) ≥ ((ρπR^2 L((L/2)))/(m+ρπR^2 L)) let πR^2 L = c , then (m+ρc)^2 ≥σρc^2 ⇒ m≥((√(σρ)) )c−ρc ⇒ m_(minimum) =((√(σρ))−ρ)πR^2 L .

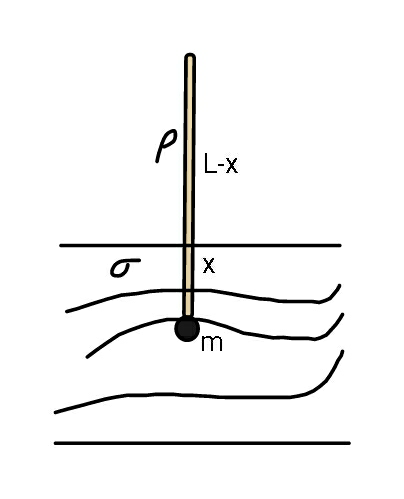
$$\mathrm{for}\:\mathrm{stability}\: \\ $$$$\mathrm{centre}\:\mathrm{of}\:\mathrm{buoyancy}\:\mathrm{must}\:\mathrm{be}\:\mathrm{above} \\ $$$$\mathrm{or}\:\mathrm{at}\:\mathrm{same}\:\mathrm{level}\:\mathrm{as}\:\mathrm{centre}\:\mathrm{of}\:\mathrm{gravity}. \\ $$$$\Rightarrow\:\:\:\frac{\mathrm{x}}{\mathrm{2}}\geqslant\frac{\mathrm{m}×\mathrm{0}+\rho\pi\mathrm{R}^{\mathrm{2}} \mathrm{L}\left(\frac{\mathrm{L}}{\mathrm{2}}\right)}{\mathrm{m}+\rho\pi\mathrm{R}^{\mathrm{2}} \mathrm{L}} \\ $$$$\mathrm{and}\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\mathrm{m}+\rho\pi\mathrm{R}^{\mathrm{2}} \mathrm{L}=\sigma\pi\mathrm{R}^{\mathrm{2}} \mathrm{x} \\ $$$$\Rightarrow\:\:\frac{\mathrm{m}+\rho\pi\mathrm{R}^{\mathrm{2}} \mathrm{L}}{\mathrm{2}\sigma\pi\mathrm{R}^{\mathrm{2}} }\:\geqslant\:\frac{\rho\pi\mathrm{R}^{\mathrm{2}} \mathrm{L}\left(\frac{\mathrm{L}}{\mathrm{2}}\right)}{\mathrm{m}+\rho\pi\mathrm{R}^{\mathrm{2}} \mathrm{L}} \\ $$$$\mathrm{let}\:\pi\mathrm{R}^{\mathrm{2}} \mathrm{L}\:=\:\mathrm{c}\:,\:\mathrm{then} \\ $$$$\:\:\:\:\:\:\:\left(\mathrm{m}+\rho\mathrm{c}\right)^{\mathrm{2}} \:\geqslant\sigma\rho\mathrm{c}^{\mathrm{2}} \\ $$$$\Rightarrow\:\:\:\:\:\mathrm{m}\geqslant\left(\sqrt{\sigma\rho}\:\right)\mathrm{c}−\rho\mathrm{c} \\ $$$$\Rightarrow\:\:\:\:\mathrm{m}_{\mathrm{minimum}} =\left(\sqrt{\sigma\rho}−\rho\right)\pi\mathrm{R}^{\mathrm{2}} \mathrm{L}\:. \\ $$

Commented by Tinkutara last updated on 30/Mar/19

Thank you Sir! But what was wrong with previous answer?

Commented by ajfour last updated on 30/Mar/19

previous answer should go for maximum mass that be attached to stick to keep it afloat still, i think.

$$\mathrm{previous}\:\mathrm{answer}\:\mathrm{should}\:\mathrm{go}\:\mathrm{for} \\ $$$$\mathrm{maximum}\:\mathrm{mass}\:\mathrm{that}\:\mathrm{be}\:\mathrm{attached} \\ $$$$\mathrm{to}\:\mathrm{stick}\:\mathrm{to}\:\mathrm{keep}\:\mathrm{it}\:\mathrm{afloat}\:\mathrm{still},\:\mathrm{i}\:\mathrm{think}. \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply