Question Number 57212 by Tinkutara last updated on 31/Mar/19
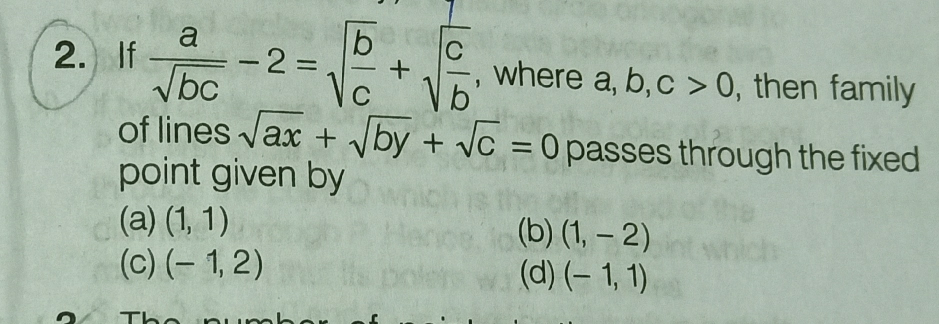
Answered by ajfour last updated on 31/Mar/19
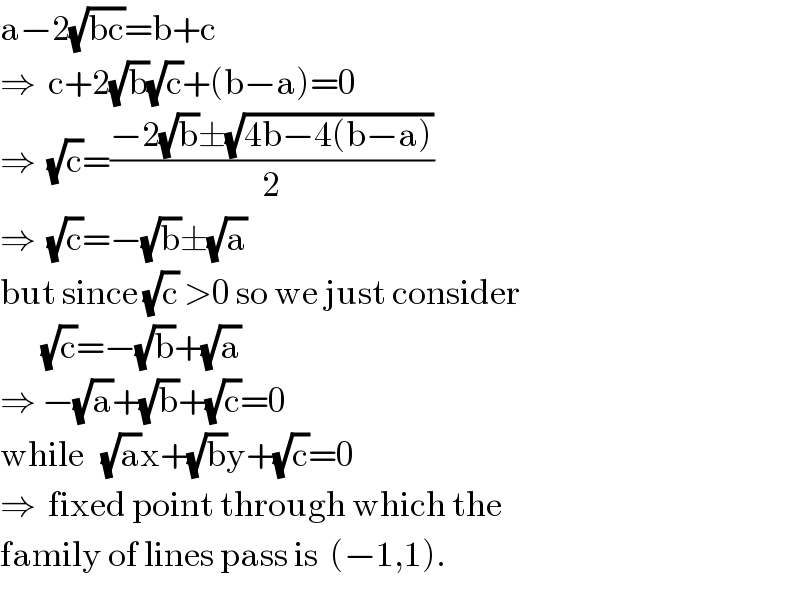
$$\mathrm{a}−\mathrm{2}\sqrt{\mathrm{bc}}=\mathrm{b}+\mathrm{c} \\ $$$$\Rightarrow\:\:\mathrm{c}+\mathrm{2}\sqrt{\mathrm{b}}\sqrt{\mathrm{c}}+\left(\mathrm{b}−\mathrm{a}\right)=\mathrm{0} \\ $$$$\Rightarrow\:\:\sqrt{\mathrm{c}}=\frac{−\mathrm{2}\sqrt{\mathrm{b}}\pm\sqrt{\mathrm{4b}−\mathrm{4}\left(\mathrm{b}−\mathrm{a}\right)}}{\mathrm{2}} \\ $$$$\Rightarrow\:\:\sqrt{\mathrm{c}}=−\sqrt{\mathrm{b}}\pm\sqrt{\mathrm{a}} \\ $$$$\mathrm{but}\:\mathrm{since}\:\sqrt{\mathrm{c}}\:>\mathrm{0}\:\mathrm{so}\:\mathrm{we}\:\mathrm{just}\:\mathrm{consider} \\ $$$$\:\:\:\:\:\:\:\sqrt{\mathrm{c}}=−\sqrt{\mathrm{b}}+\sqrt{\mathrm{a}} \\ $$$$\Rightarrow\:−\sqrt{\mathrm{a}}+\sqrt{\mathrm{b}}+\sqrt{\mathrm{c}}=\mathrm{0} \\ $$$$\mathrm{while}\:\:\:\sqrt{\mathrm{a}}\mathrm{x}+\sqrt{\mathrm{b}}\mathrm{y}+\sqrt{\mathrm{c}}=\mathrm{0} \\ $$$$\Rightarrow\:\:\mathrm{fixed}\:\mathrm{point}\:\mathrm{through}\:\mathrm{which}\:\mathrm{the} \\ $$$$\mathrm{family}\:\mathrm{of}\:\mathrm{lines}\:\mathrm{pass}\:\mathrm{is}\:\:\left(−\mathrm{1},\mathrm{1}\right). \\ $$
Commented by Tinkutara last updated on 31/Mar/19
Isn't the root over x and y also?
Commented by ajfour last updated on 31/Mar/19
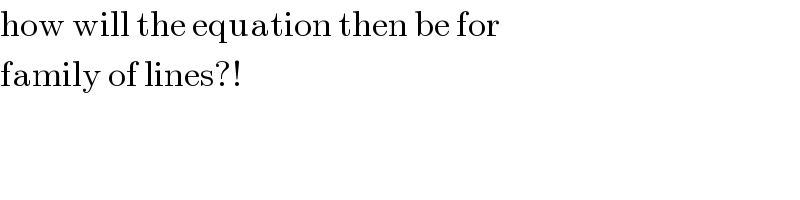
$$\mathrm{how}\:\mathrm{will}\:\mathrm{the}\:\mathrm{equation}\:\mathrm{then}\:\mathrm{be}\:\mathrm{for} \\ $$$$\mathrm{family}\:\mathrm{of}\:\mathrm{lines}?! \\ $$
Commented by Tinkutara last updated on 01/Apr/19
Yes Sir, Thanks a lot!
