Question Number 57296 by mr W last updated on 01/Apr/19
Commented by mr W last updated on 01/Apr/19

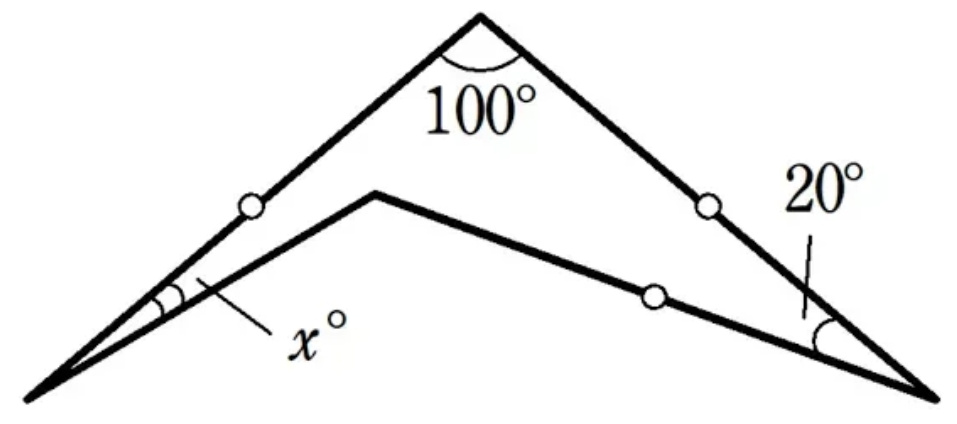
$${Find}\:{x}=? \\ $$
Answered by MJS last updated on 02/Apr/19

$${A}=\begin{pmatrix}{−{a}}\\{\mathrm{0}}\end{pmatrix}\:{B}=\begin{pmatrix}{\mathrm{0}}\\{\mathrm{0}}\end{pmatrix}\:{C}=\begin{pmatrix}{−{b}\mathrm{cos}\:\mathrm{40}°}\\{{b}\mathrm{sin}\:\mathrm{40}°}\end{pmatrix}\:{D}=\begin{pmatrix}{−{b}\mathrm{cos}\:\mathrm{20}°}\\{{b}\mathrm{sin}\:\mathrm{20}°}\end{pmatrix} \\ $$$$\mathrm{line}\:{AD}:\:\mathfrak{y}=\frac{{b}\mathrm{sin}\:\mathrm{20}°}{{a}−{b}\mathrm{cos}\:\mathrm{20}°}\mathfrak{x}+\frac{{ab}\mathrm{sin}\:\mathrm{20}°}{{a}−{b}\mathrm{cos}\:\mathrm{20}°}\:\Rightarrow \\ $$$$\Rightarrow\:{x}=\mathrm{40}°−\mathrm{arctan}\:\frac{{b}\mathrm{sin}\:\mathrm{20}°}{{a}−{b}\mathrm{cos}\:\mathrm{20}°} \\ $$$${a}={b}\frac{\mathrm{sin}\:\mathrm{100}°}{\mathrm{sin}\:\mathrm{40}°} \\ $$$${x}=\mathrm{40}°−\mathrm{arctan}\:\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\:=\mathrm{10}° \\ $$
Commented by mr W last updated on 02/Apr/19
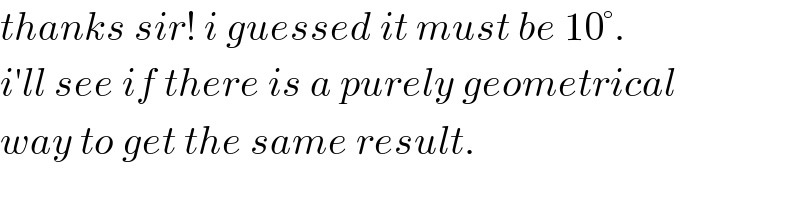
$${thanks}\:{sir}!\:{i}\:{guessed}\:{it}\:{must}\:{be}\:\mathrm{10}°. \\ $$$${i}'{ll}\:{see}\:{if}\:{there}\:{is}\:{a}\:{purely}\:{geometrical} \\ $$$${way}\:{to}\:{get}\:{the}\:{same}\:{result}. \\ $$
Commented by MJS last updated on 02/Apr/19

$$\mathrm{I}'\mathrm{m}\:\mathrm{always}\:\mathrm{fast}\:\mathrm{with}\:\mathrm{coordinates},\:\mathrm{but}\:\mathrm{there} \\ $$$$\mathrm{should}\:\mathrm{be}\:\mathrm{other}\:\mathrm{possibilities}… \\ $$
