Menu Close

Question-57306

Tinku Tara 0 Comments
Pin




Question Number 57306 by Aditya789 last updated on 02/Apr/19
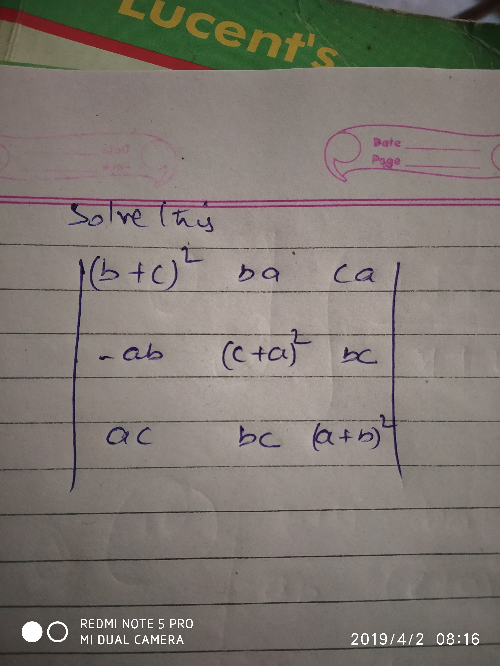
Commented by tanmay.chaudhury50@gmail.com last updated on 02/Apr/19
is it ab or −ab
$${is}\:{it}\:{ab}\:\:{or}\:−{ab}\:\: \\ $$
Commented by Aditya789 last updated on 02/Apr/19
ab
$$\mathrm{ab} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 02/Apr/19
△ =determinant the degree of △=6 now when we put a=0 △=0 so a is factor of△ similarly if b=0 then △=0 so b is factor of △ when c=0 then △=0 so c isfactor of △ now put a+b+c=0 that means in place of (b+c) put(−a) in place of (c+a) put (−b) and in place of (a+b) put (−c) △=∣(b+c)^2 ba ca∣ (put a+b+c=0) ∣ab (c+a)^2 bc∣ ∣ac bc (a+b)^2 ∣ = ∣(−a)^2 ba ca∣ ∣ab (−b)^2 bc∣ ∣ac bc (−c)^2 ∣ abc∣a b c∣ ∣a b c∣ ∣a b c∣ look three rows so △=0 so (a+b+c) is also a factor... now when we put (a+b+c)=0 three rows becomd identical hence by rule (a+b+c)^2 is also a factor △=kabc(a+b+c)(a+b+c)^2 △=kabc(a+b+c)^3 now our task is to find value of k △=∣(b+c)^2 ba ca∣ ∣ab (c+a)^2 bc∣=kabc(a+b+c)^3 ∣ac bc (a+b)^2 ∣ put a=1 ,b=1 and c=1 both side ∣4 1 1∣ ∣1 4 1∣ ∣1 1 4∣ =k×1×1×1(1+1+1)^3 54=27k so k=2 so answer of determinat is 2abc(a+b+c)^3
$$\bigtriangleup\:={determinant} \\ $$$${the}\:{degree}\:{of}\:\bigtriangleup=\mathrm{6} \\ $$$${now}\:\:{when}\:{we}\:{put}\:{a}=\mathrm{0}\:\:\:\:\:\bigtriangleup=\mathrm{0}\:{so}\:{a}\:{is}\:{factor}\:{of}\bigtriangleup \\ $$$${similarly}\:{if}\:{b}=\mathrm{0}\:\:{then}\:\bigtriangleup=\mathrm{0}\:{so}\:{b}\:{is}\:{factor}\:{of}\:\bigtriangleup \\ $$$${when}\:{c}=\mathrm{0}\:\:{then}\:\bigtriangleup=\mathrm{0}\:\:{so}\:{c}\:{isfactor}\:{of}\:\bigtriangleup \\ $$$${now}\: \\ $$$${put}\:{a}+{b}+{c}=\mathrm{0}\:{that}\:{means}\:{in}\:{place}\:{of}\:\left({b}+{c}\right)\:{put}\left(−{a}\right) \\ $$$${in}\:{place}\:{of}\:\left({c}+{a}\right)\:{put}\:\left(−{b}\right)\:{and}\:{in}\:{place}\:{of}\:\left({a}+{b}\right)\:{put} \\ $$$$\left(−{c}\right) \\ $$$$\bigtriangleup=\mid\left({b}+{c}\right)^{\mathrm{2}} \:\:\:\:{ba}\:\:\:\:\:\:\:\:\:\:\:\:{ca}\mid\:\left({put}\:{a}+{b}+{c}=\mathrm{0}\right) \\ $$$$\:\:\:\:\:\:\:\:\mid{ab}\:\:\:\:\:\:\:\:\left({c}+{a}\right)^{\mathrm{2}} \:\:\:\:\:\:\:\:\:{bc}\mid \\ $$$$\:\:\:\:\:\:\:\:\mid{ac}\:\:\:\:\:\:\:\:{bc}\:\:\:\:\:\:\:\:\left({a}+{b}\right)^{\mathrm{2}} \mid \\ $$$$=\:\:\:\:\mid\left(−{a}\right)^{\mathrm{2}} \:\:\:\:\:{ba}\:\:\:\:\:\:\:\:\:{ca}\mid \\ $$$$\:\:\:\:\:\:\:\mid{ab}\:\:\:\:\:\:\:\:\:\:\:\:\:\left(−{b}\right)^{\mathrm{2}} \:\:\:\:{bc}\mid \\ $$$$\:\:\:\:\:\:\:\mid{ac}\:\:\:\:\:\:\:\:\:\:\:\:{bc}\:\:\:\:\:\:\:\:\:\:\left(−{c}\right)^{\mathrm{2}} \mid \\ $$$${abc}\mid{a}\:\:\:\:\:{b}\:\:\:\:\:\:\:{c}\mid \\ $$$$\:\:\:\:\:\:\:\mid{a}\:\:\:\:\:{b}\:\:\:\:\:\:\:\:{c}\mid \\ $$$$\:\:\:\:\:\:\:\mid{a}\:\:\:\:\:{b}\:\:\:\:\:\:\:\:{c}\mid \\ $$$${look}\:{three}\:\:{rows}\: \\ $$$$\boldsymbol{{so}}\:\bigtriangleup=\mathrm{0} \\ $$$$\:{so}\:\left({a}+{b}+{c}\right)\:{is}\:{also}\:{a}\:{factor}… \\ $$$${now}\:{when}\:{we}\:{put}\:\left({a}+{b}+{c}\right)=\mathrm{0} \\ $$$$\:{three}\:{rows}\:{becomd}\:{identical}\: \\ $$$${hence}\:{by}\:{rule}\:\left({a}+{b}+{c}\right)^{\mathrm{2}} {is}\:{also}\:{a}\:{factor} \\ $$$$\bigtriangleup={kabc}\left({a}+{b}+{c}\right)\left({a}+{b}+{c}\right)^{\mathrm{2}} \\ $$$$\bigtriangleup={kabc}\left({a}+{b}+{c}\right)^{\mathrm{3}} \\ $$$${now}\:{our}\:{task}\:{is}\:{to}\:{find}\:{value}\:{of}\:{k} \\ $$$$\bigtriangleup=\mid\left({b}+{c}\right)^{\mathrm{2}} \:\:\:{ba}\:\:\:\:\:\:\:\:\:\:\:{ca}\mid \\ $$$$\:\:\:\:\:\:\:\:\mid{ab}\:\:\:\:\:\:\left({c}+{a}\right)^{\mathrm{2}} \:\:\:\:\:\:\:\:\:\:{bc}\mid={kabc}\left({a}+{b}+{c}\right)^{\mathrm{3}} \\ $$$$\:\:\:\:\:\:\:\mid{ac}\:\:\:\:\:\:\:\:{bc}\:\:\:\:\:\:\:\:\:\:\left({a}+{b}\right)^{\mathrm{2}} \mid \\ $$$${put}\:{a}=\mathrm{1}\:,{b}=\mathrm{1}\:\:{and}\:{c}=\mathrm{1}\:{both}\:{side} \\ $$$$\mid\mathrm{4}\:\:\:\:\mathrm{1}\:\:\:\:\mathrm{1}\mid \\ $$$$\mid\mathrm{1}\:\:\:\:\mathrm{4}\:\:\:\:\:\mathrm{1}\mid \\ $$$$\mid\mathrm{1}\:\:\:\:\mathrm{1}\:\:\:\:\:\mathrm{4}\mid\:\:\:={k}×\mathrm{1}×\mathrm{1}×\mathrm{1}\left(\mathrm{1}+\mathrm{1}+\mathrm{1}\right)^{\mathrm{3}} \\ $$$$ \\ $$$$\mathrm{54}=\mathrm{27}{k}\:\:{so}\:{k}=\mathrm{2} \\ $$$$\boldsymbol{{so}}\:\boldsymbol{{answer}}\:\boldsymbol{{of}}\:\boldsymbol{{determinat}}\:\boldsymbol{{is}}\:\mathrm{2}\boldsymbol{{abc}}\left(\boldsymbol{{a}}+\boldsymbol{{b}}+\boldsymbol{{c}}\right)^{\mathrm{3}} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$$$ \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 02/Apr/19
Commented by rahul 19 last updated on 02/Apr/19
Very helpful sir!
$${Very}\:{helpful}\:{sir}! \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 02/Apr/19
thank you ...source higher algebra 1)Bernard and child 2)Hall and knight famous books...
$${thank}\:{you}\:…{source}\:{higher}\:{algebra} \\ $$$$\left.\mathrm{1}\right){Bernard}\:{and}\:{child} \\ $$$$\left.\mathrm{2}\right){Hall}\:{and}\:{knight} \\ $$$${famous}\:{books}… \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *